二叉树是算法世界的核心骨架,更是大厂面试的必考点!本文用2000字+6张图解+5段代码,带你彻底掌握二叉树的结构原理、遍历方法和堆排序实现,从此算法面试不再慌!
目录
一、二叉树:数据结构中的“黄金骨架”
1.1 核心定义与特性
二、二叉树的两种存储方式
2.1 链式存储(主流方式)
2.2 顺序存储(适合完全二叉树)
三、二叉树遍历:三大经典方式(附动图解析)
3.1 遍历方式对比
四、堆与堆排序:二叉树的高效应用
4.1 堆的本质
4.2 堆排序四步法
五、二叉树实战应用场景
六、面试高频考点解析
最后挑战:
一、二叉树:数据结构中的“黄金骨架”
1.1 核心定义与特性
-
层级结构:每个节点最多有两个子节点(左/右子树)
-
逻辑关系:节点间存在父子层级关系(根节点、叶节点等)
-
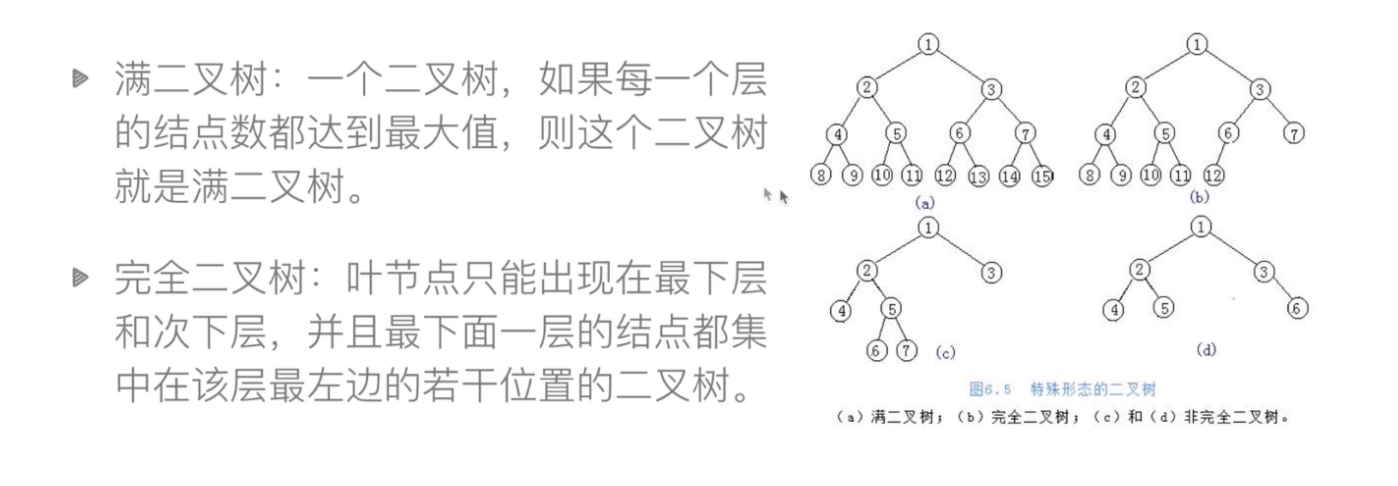
特殊形态:
-
完全二叉树:除最后一层外全满,最后一层节点从左向右连续排列
-
二叉搜索树(BST):左子树 < 根节点 < 右子树
-
平衡二叉树(AVL/红黑树):通过旋转保持左右子树高度差≤1
-

完全二叉树示例:节点按层级从左到右连续排列
二、二叉树的两种存储方式
2.1 链式存储(主流方式)
class Node:
def __init__(self, data):
self.data = data # 数据域
self.lchild = None # 左子节点指针
self.rchild = None # 右子节点指针
-
优势:灵活处理非完全二叉树
-
缺点:额外存储指针空间
2.2 顺序存储(适合完全二叉树)
# 用数组存储完全二叉树
heap = [None, 'A', 'B', 'C', 'D', 'E', 'F', 'G']
# 下标关系:
# 节点i的父节点 = i//2
# 左子节点 = 2*i
# 右子节点 = 2*i+1
-
适用场景:堆结构(大顶堆/小顶堆)
-
优势:省指针空间,快速定位父子节点
三、二叉树遍历:三大经典方式(附动图解析)
3.1 遍历方式对比
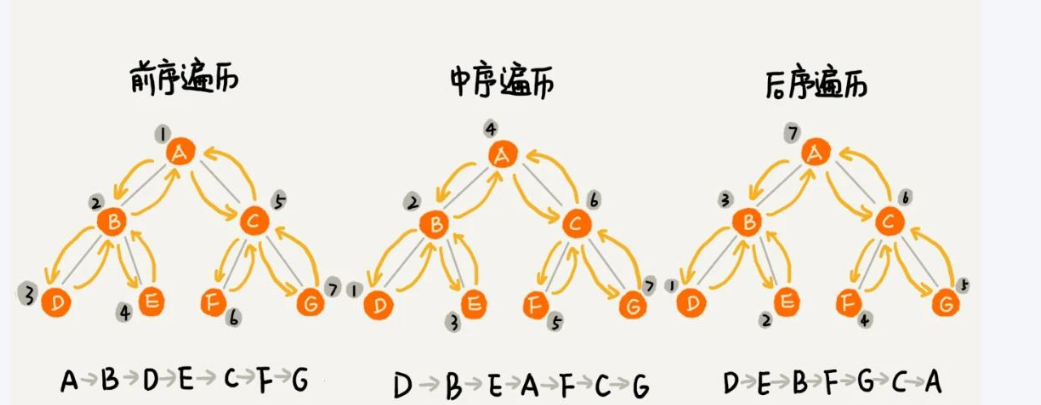
| 前序遍历 | 根 → 左 → 右 | 复制二叉树结构 |
| 中序遍历 | 左 → 根 → 右 | 二叉搜索树获取有序序列 |
| 后序遍历 | 左 → 右 → 根 | 释放二叉树内存 |
class Node():
def __init__(self, data):
self.data = data
self.lchild = None
self.rchild = None
class Tree():
def __init__(self):
self.root = None
def add(self,data):
node = Node(data)
if self.root is None:
self.root = node
return
queue = [self.root]
while queue:
cur_node = queue.pop(0)
if cur_node.lchild is None:
cur_node.lchild = node
return
else:
queue.append(cur_node.lchild)
if cur_node.rchild is None:
cur_node.rchild = node
return
else:
queue.append(cur_node.rchild)
#遍历
#前序
def front(self,node):
if node is None:
return
print(node.data, end=" ")
self.front(node.lchild)
self.front(node.rchild)
#中序
def inorder(self,node):
if node is None:
return
self.inorder(node.lchild)
print(node.data, end=" ")
self.inorder(node.rchild)
#后序
def afterorder(self,node):
if node is None:
return
self.afterorder(node.lchild)
self.afterorder(node.rchild)
print(node.data, end=" ")
if __name__ == '__main__':
tree = Tree()
tree.add("A")
tree.add("B")
tree.add("C")
tree.add("D")
tree.add("E")
tree.add("F")
tree.add("G")
tree.front(tree.root)
print()
tree.inorder(tree.root)
print()
tree.afterorder(tree.root)
四、堆与堆排序:二叉树的高效应用
4.1 堆的本质
-
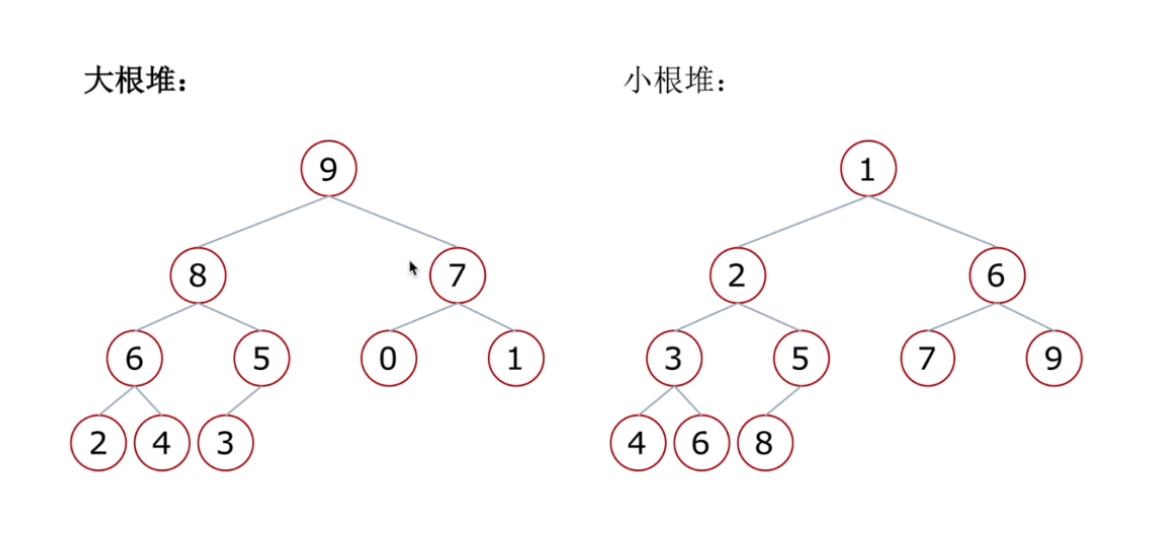
大顶堆:父节点值 ≥ 子节点值(根节点最大)
- 小顶堆:父节点值 ≤ 子节点值(根节点最小)
4.2 堆排序四步法
建堆:将无序数组调整为堆结构
取顶:堆顶元素(当前最大值)交换到数组末尾
调整:对剩余元素重新调整为堆
重复:直到堆中只剩一个元素
def heapify(arr, n, i):
"""堆的向下调整"""
largest = i
left = 2 * i + 1
right = 2 * i + 2
if left < n and arr[left] > arr[largest]:
largest = left
if right < n and arr[right] > arr[largest]:
largest = right
if largest != i:
arr[i], arr[largest] = arr[largest], arr[i]
heapify(arr, n, largest) # 递归调整子堆
def heap_sort(arr):
n = len(arr)
# 建堆(从最后一个非叶节点开始)
for i in range(n//2 – 1, -1, -1):
heapify(arr, n, i)
# 逐个提取元素
for i in range(n-1, 0, -1):
arr[0], arr[i] = arr[i], arr[0] # 交换堆顶和末尾
heapify(arr, i, 0) # 调整剩余堆
# 测试
arr = [12, 11, 13, 5, 6, 7]
heap_sort(arr)
print("排序结果:", arr) # 输出:[5, 6, 7, 11, 12, 13]
五、二叉树实战应用场景
数据库索引:B+树加速百万级数据检索
文件系统:目录树结构管理文件层级
游戏开发:场景树管理渲染对象
压缩算法:哈夫曼树实现无损压缩
任务调度:堆结构实现优先级队列
性能对比表:
| 数据检索 | O(log n) | 二叉搜索树 |
| 最大值获取 | O(1) | 大顶堆 |
| 动态增删节点 | O(log n) | 平衡二叉树(AVL) |
| 层级数据处理 | O(n) | 普通二叉树遍历 |
六、面试高频考点解析
如何判断完全二叉树?
-
层序遍历,遇到空节点后不应再出现非空节点
为什么数据库用B+树不用二叉树?
-
B+树矮胖结构减少磁盘IO(二叉树在数据量大时高度激增)
手写非递归遍历实现
# 前序遍历的非递归实现(使用栈)
def preorder_iterative(root):
stack = [root]
while stack:
node = stack.pop()
if node:
print(node.data, end=" ")
stack.append(node.rchild) # 右子先入栈
stack.append(node.lchild) # 左子后入栈(先出)
最后挑战:
如何用O(1)空间复杂度实现Morris中序遍历?评论区留下你的思路!
资源推荐:
《算法导论》第6章 – 堆排序与二叉树
VisuAlgo.net – 二叉树动态可视化工具
LeetCode二叉树专题 – 精选50题训练
 网硕互联帮助中心
网硕互联帮助中心





评论前必须登录!
注册