LMS(最小均方)算法是一种自适应滤波算法,通过迭代调整滤波器系数以最小化输出信号的均方误差。在转子不平衡控制中,用于滤除与旋转频率同频的共振信号。
一、算法原理
核心方程:
-
滤波器输出:
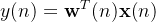
-
误差信号:
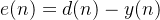
-
权值更新:
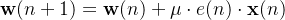
关键参数:
-
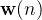 :滤波器权值向量
:滤波器权值向量 -
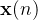 :输入信号向量
:输入信号向量 -
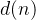 :期望信号(含噪声的振动信号)
:期望信号(含噪声的振动信号) -
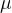 :步长因子(收敛速度与稳定性的平衡)
:步长因子(收敛速度与稳定性的平衡)
同频共振消除原理:
-
使用正交参考信号
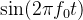 ,
,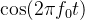 作为输入
作为输入 -
自适应调整权值,使输出
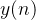 逼近同频干扰分量
逼近同频干扰分量 -
误差信号
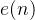 即为滤除同频干扰后的振动信号
即为滤除同频干扰后的振动信号
二、MATLAB仿真验证
% LMS算法消除转子同频共振 – MATLAB仿真
clear; clc; close all;
% 参数设置
fs = 1000; % 采样频率 (Hz)
f0 = 50; % 转子旋转频率 (Hz)
T = 1; % 信号时长 (s)
t = 0:1/fs:T-1/fs; % 时间向量
N = length(t); % 样本数
% 生成转子振动信号 (含同频共振和噪声)
resonance = 1.2*sin(2*pi*f0*t + pi/4) + 0.8*cos(2*pi*f0*t); % 同频共振
noise = 0.5*randn(1,N); % 高斯白噪声
d = resonance + noise; % 观测信号
% 生成参考信号 (正交基)
x_sin = sin(2*pi*f0*t);
x_cos = cos(2*pi*f0*t);
% LMS参数初始化
mu = 0.02; % 步长因子
w_sin = 0; % 正弦分量权值
w_cos = 0;
 网硕互联帮助中心
网硕互联帮助中心

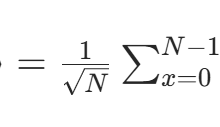


评论前必须登录!
注册