文章目录
- 【算法】堆(Heap)的概念、懒删除与堆排序
-
- 1. 堆的概念
-
- 1.1 堆的特点
- 1.2 堆的存储
- 1.3 堆的操作
-
- 1.3.1 构建
- 1.3.2 插入
- 1.3.3 删除
- 1.3.4 访问最大值
- 2. 堆的懒删除(Lazy Deletion)
-
- 2.1 删除第
x
x
x 个插入堆的元素 - 2.2 删除元素
x
x
x
- 2.1 删除第
- 3. 堆排序(Heap Sort)
-
- 3.1 回顾选择排序
- 3.2 堆排序
【算法】堆(Heap)的概念、懒删除与堆排序
堆,这是一种高级数据结构,可以在一堆数中找到最大值或最小值,它是树形结构,普遍是完全二叉树。它还可以进行排序、选择之类的操作
1. 堆的概念
堆(Heap),这是一种高级数据结构,一般情况下堆是一种完全二叉树,它称为二叉堆,这篇文章我们默认堆为二叉堆
1.1 堆的特点
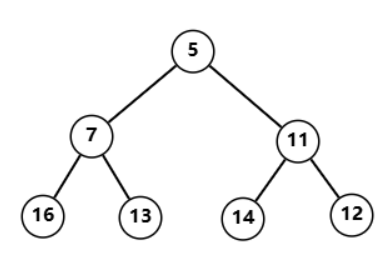 上图是一个小根堆(小顶堆),小根堆的根节点对应值最小,且每一条从上到下的路径都是升序的
上图是一个小根堆(小顶堆),小根堆的根节点对应值最小,且每一条从上到下的路径都是升序的
5 -> 7 -> 16
5 -> 7 -> 13
5 -> 11 -> 14
5 -> 11 -> 12
为什么有序呢?你还会发现第三个特点,小根堆任意一个节点的左孩子与右孩子都小于等于它自己。例如根节点左孩子与右孩子小于根节点,左孩子的左孩子和右孩子也小于左孩子,右孩子的左孩子和右孩子还小于右孩子……
反之,大顶堆的根节点值最大,每一条从上到下的路径都是降序的,任意一个节点大于左右孩子
不过正因为这样的套娃,也让堆这种结构出现,且插入删除时间复杂度均为
Θ
(
n
log
n
)
\\Theta(n\\log n)
Θ(nlogn)
1.2 堆的存储
可能有的人会想到树的树形存储——数据、左孩子节点指针、右孩子节点指针、父节点指针。其实这个没有必要,正因为这是一个完全二叉树,且中间没有空隙,所以我们可以用顺序表存储方法,也就是堆长这样,顺序表长这样(下标从
1
1
1 开始) 
| 数据 | 5 | 7 | 11 | 16 | 13 | 14 | 12 |
还记得顺序表存储树的访问方式吗? 根节点下表为
1
1
1 ,下标为
x
x
x 的节点左孩子下标为
2
x
2x
2x,右孩子为
2
x
+
1
2x+1
2x+1,父节点为
⌊
x
2
⌋
\\lfloor\\cfrac x 2\\rfloor
⌊2x⌋
1.3 堆的操作
1.3.1 构建
构建操作是给出一个顺序表,让你将其构建为一个大根堆/小根堆,这里我们都以大顶堆为例,小顶堆就结合思路理解,包括后面的插入、删除、询问操作
我们知道大顶堆有一个最大的特点,就是每一个节点大于左右孩子。那么我们先将顺序表变成完全二叉树的结构(但是存储结构上完全不变,现在讲的是逻辑,手写后面讲)
例如这么一个顺序表
| 数据 | 38 | 78 | 66 | 20 | 48 | 91 | 39 | 50 | 82 |
就可以变成这样 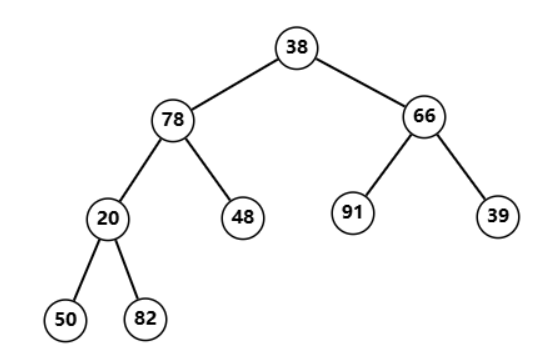 随后从树的 BFS 序中最后一个父节点(也就是最后一个节点的父节点)开始,不断调整,调整完后再到倒数第二个父节点、倒数第三、倒数第四……直到遍历完根节点,每次将自己与左右节点进行比较,如果自己大于左右节点那就不管了,否则找到最大的那个节点,与其进行交换,再跳到交换后的原节点继续调整,直到自己大于左右节点
随后从树的 BFS 序中最后一个父节点(也就是最后一个节点的父节点)开始,不断调整,调整完后再到倒数第二个父节点、倒数第三、倒数第四……直到遍历完根节点,每次将自己与左右节点进行比较,如果自己大于左右节点那就不管了,否则找到最大的那个节点,与其进行交换,再跳到交换后的原节点继续调整,直到自己大于左右节点
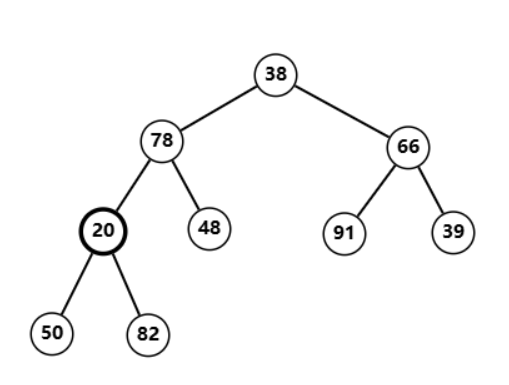 调整
调整
20
20
20,发现不符合堆性质 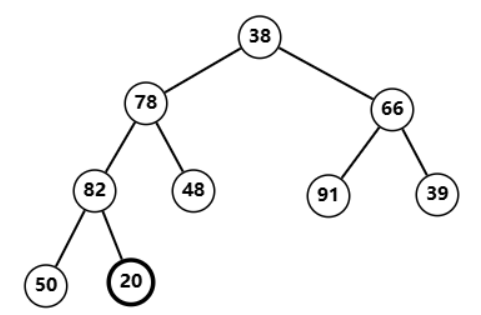 将
将
82
82
82 与
20
20
20 对调,
20
20
20 恢复堆性质 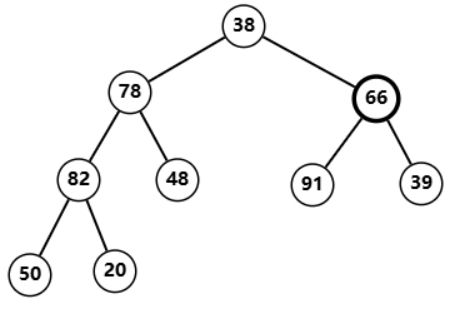 调整
调整
66
66
66 发现也不符合性质 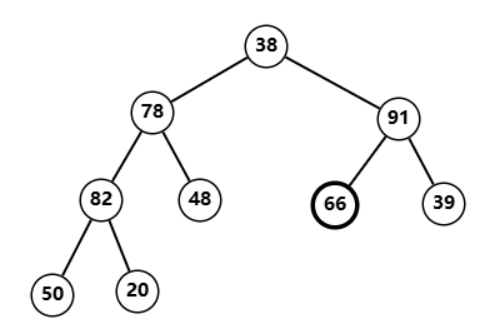 与
与
91
91
91 对调后发现堆性质恢复 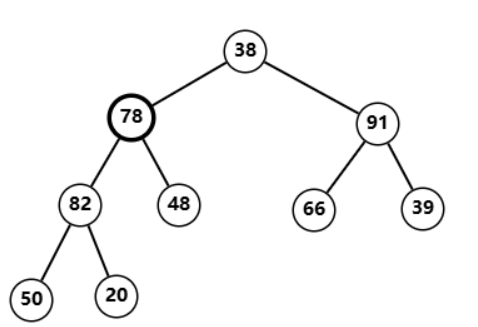
78
78
78 任旧不符合堆性质 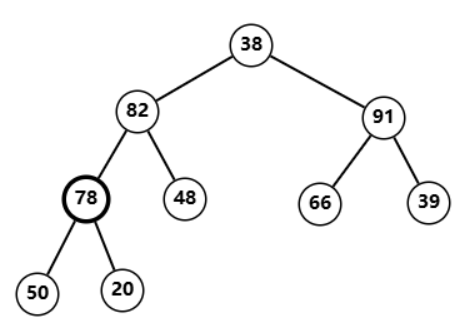 与
与
82
82
82 交换后恢复性质 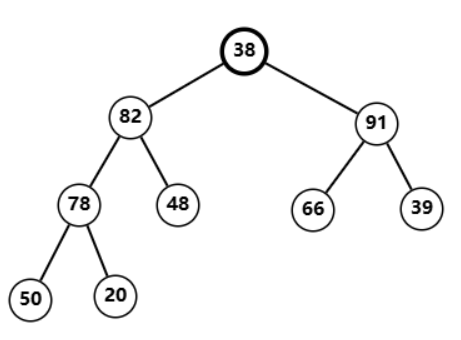 调整
调整
38
38
38 发现也不符合堆性质 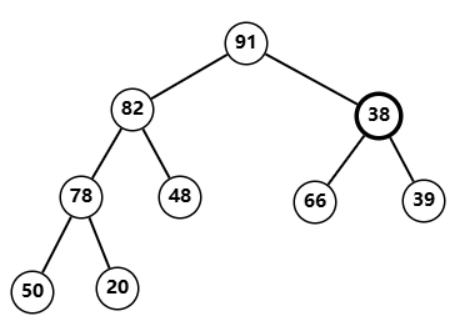 与
与
91
91
91 交换后发现不符合堆性质
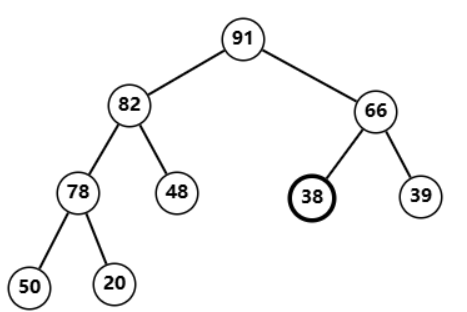 与
与
66
66
66 交换后调整完毕,同时堆构建完成
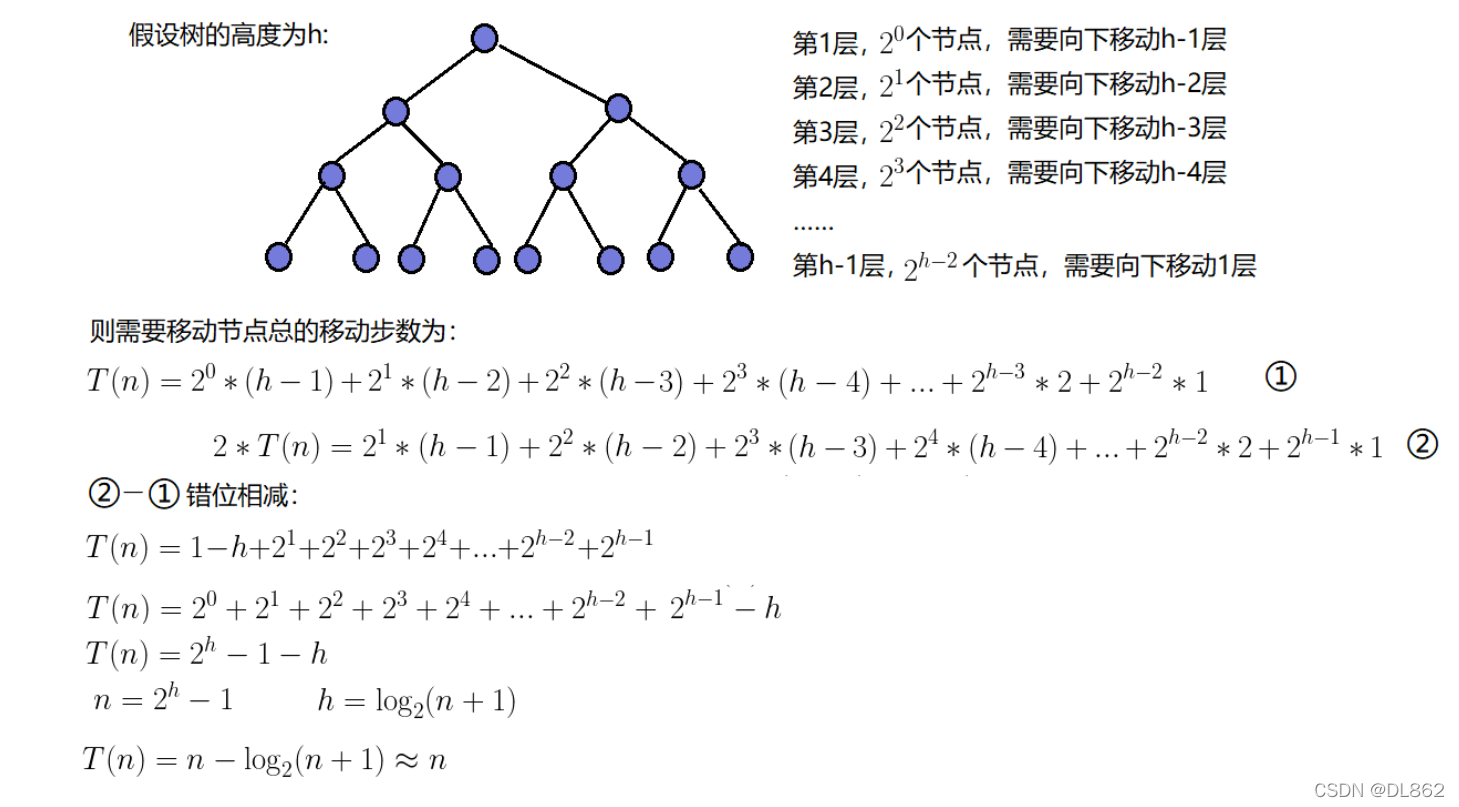
这个操作的的时间复杂度为
Θ
(
n
)
\\Theta(n)
Θ(n),有的人(比如我)以前认为时间复杂度应该是
Θ
(
n
log
n
)
\\Theta(n \\log n)
Θ(nlogn)
不过,这个有自己的数学证明过程
 不过,在实际操作中,堆中的元素会根据访问公式来进行调整
不过,在实际操作中,堆中的元素会根据访问公式来进行调整
1.3.2 插入
那么,在堆中又应该如何插入元素呢?首先,将元素放在顺序表最后,也就是大小
+
1
+1
+1 的位置,插入过后,将自己与自己的父亲进行比较,如果比父亲大就与父亲对调,调换后继续与自己父亲比较,直到自己比父亲小或等于为止,这个很类似于插入排序的过程
例如在这个堆中插入节点
88
88
88 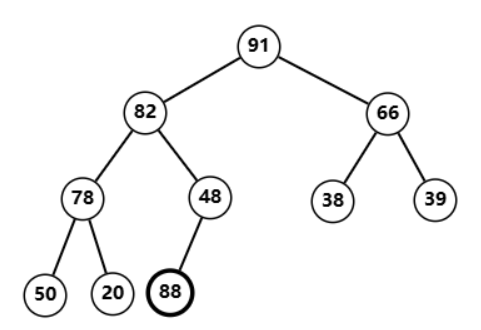 插入过后,
插入过后,
88
88
88 比父节点
48
48
48 大 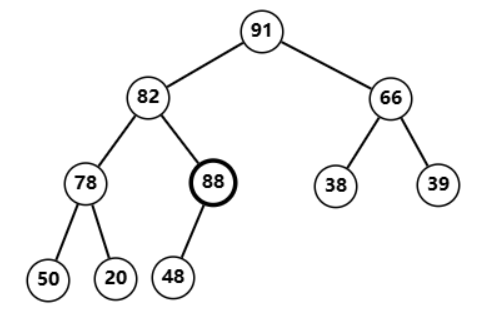 对调过后自己依旧比父节点
对调过后自己依旧比父节点
82
82
82 大 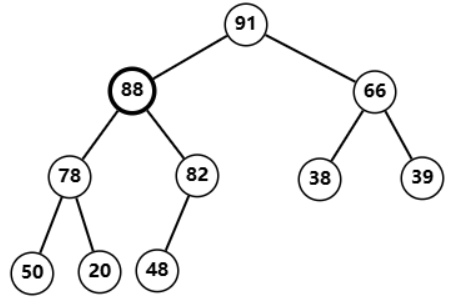 再次对调,
再次对调,
88
88
88 比父节点
91
91
91 小,调整完毕
这种操作时间复杂度为
Θ
(
log
n
)
\\Theta(\\log n)
Θ(logn),因为最差情况是插入了一个比堆顶还大的数字,随后一路向上到根节点
1.3.3 删除
在堆中,删除元素一般只删除堆顶,而删除堆中某个元素的方法会在这一章讲到
删除元素又应该咋办呢?直接删了调整起来不仅不知道如何调整,而且堆根节点都没了又应该咋整
我们应该换位思考,可以将堆的最后一层的最后一个(也就是顺序表最后一项)元素赋值给第一个元素,然后把它自己删掉。这样,头没有缺失,也很好修改了
那么这个又应该如何修改呢?首先,将末尾替换给头后删除,随后将头作为当前节点,与自己的左右孩子比较。如果当前节点大于等于左右孩子,那么调整完成;否则就让当前节点与左右孩子中最大的那个节点与其对调,对调后继续看是否满足堆的性质,直到成功满足为之
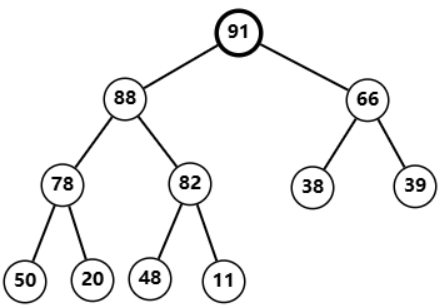 删除堆顶
删除堆顶
91
91
91 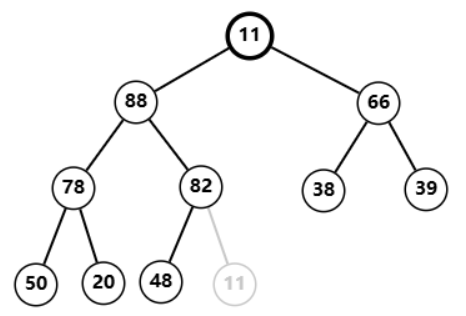 用
用
11
11
11 替换
91
91
91 后删除,发现自己小于左右孩子 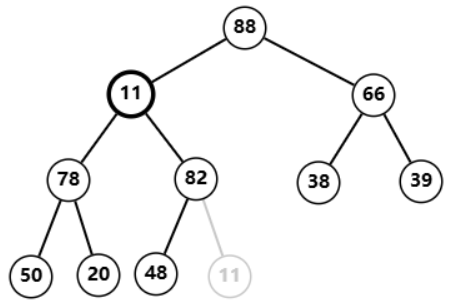
11
11
11 与
88
88
88 交换,依旧小于左右孩子 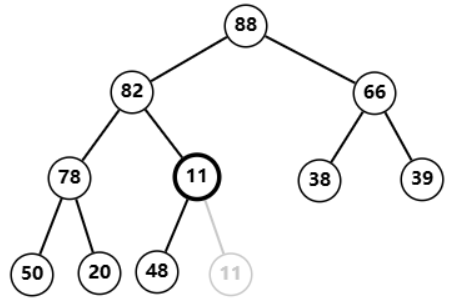 再次与
再次与
82
82
82 交换,小于左孩子 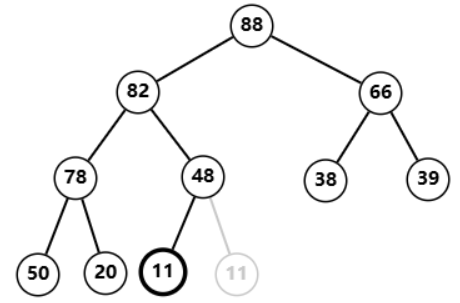 交换后成功符合堆的性质,调整完毕
交换后成功符合堆的性质,调整完毕
这个操作的时间复杂度也是
Θ
(
log
n
)
\\Theta(\\log n)
Θ(logn),但是不管咋样都是这个时间复杂度,而不像插入最利情况可以达到
Θ
(
1
)
\\Theta(1)
Θ(1),况且你删除顶堆,却用了一个层数最低的值替补,而层数高的任意一个值都大于等于层数低的任意一个值
1.3.4 访问最大值
说白了就是访问堆顶,这个很好说吧!就是访问顺序表第一项
时间复杂度
Θ
(
1
)
\\Theta(1)
Θ(1)
2. 堆的懒删除(Lazy Deletion)
有的时候,一些数据结构可以延迟做事,例如堆和线段树,就像暑假前一天使劲补作业(请勿模仿)一样,删除这件事放在询问(检查作业)时再做,这就是堆的懒删除
2.1 删除第
x
x
x 个插入堆的元素
在堆的删除操作中只能删除堆顶的元素,但是我们有没有办法让它也可以删除堆第
x
x
x 个插入的元素呢?确实有的
既然每一次询问堆中最大值/最小值,那么每一次询问就只跟堆顶有关系。所以,我们可以定义一个数组
D
D
D,
D
i
D_i
Di 表示第
i
i
i 个插入的元素是否被删除了,删除为
1
1
1,未删除为
0
0
0 。随后,如果我们想要插入一个元素,那么就给堆中插入它的插入编号与它的数据所构成的集合,比较器根据它的数据排序
随后,删除第
x
x
x 个插入堆的元素的时候,只需要标记
D
x
D_x
Dx 项为
1
1
1 就可以了
询问堆顶的时候,我们先判断堆顶元素的插入编号是否在
D
D
D 中已经被标记成了已删除状态,如果已删除那就删除堆顶,否则输出堆顶。就这么简单
2.2 删除元素
x
x
x
对于这个问题,我们称操作用的堆为
H
H
H,再维护一个用于删除的容器
D
D
D
这个有一个前提条件,那就是删除的元素是堆中出现过的
如果可以保证,我们就可以将
D
D
D 维护成堆,
H
H
H 取最大/最小,
D
D
D 也取最大和最小,那么如果相等,就抵消;如果不相等,就输出
如果不能保证,我们就可以将
D
D
D 维护成二叉(平衡)搜索树,每次取堆顶,在里面寻找有没有这个值,有的话抵消,没有的话输出
3. 堆排序(Heap Sort)
堆排序(Heap Sort)是一种不稳定排序,但是它的排序时间非常平衡,没有快速排序会被数据卡成
Θ
(
n
2
)
\\Theta(n^2)
Θ(n2) 的情况,也没有冒泡最优都
Θ
(
n
)
\\Theta(n)
Θ(n) 的情况,时间复杂度都是均衡的
Θ
(
n
log
n
)
\\Theta(n\\log n)
Θ(nlogn),这就很好
3.1 回顾选择排序
还记得选择排序的思路吗?每次在一堆数字中找到最大值,然后将最大值与顺序表最后一项交换,再排除最大值继续找,把最大值与倒数第二项交换……直到最终全部排序完毕
当然,这个也可以反着来,那就是在所有元素中找到最小值与第一项交换,再找第一项后的最小值与第二项交换……直到全部排序完 
3.2 堆排序
既然选择排序要在一堆数中找到最大值并放在最后,然后找到第二大、第三大、第四大……直到排序完毕,那么哪个容器可以高效地找到最大值再删除呢?堆!
我们可以一个顺序表构建成为一个大顶堆,随后将第一项与最后一项交换,然后“删掉”,调整,第二大又会出现,“删掉”,调整,第三大,“删掉”……最终,直到堆中什么也没有了就是排序完成了
有人可能问为什么是交换,不是替换吗?但是,我们可以维护堆顶
n
n
n,交换后删除元素就是将
n
n
n 向前挪一位而已,这也是“删掉”为什么打了引号的原因,这种操作也叫做伪删除
下一篇博文会讲与堆有关的容器/函数,堆与堆排序的手写方法
 网硕互联帮助中心
网硕互联帮助中心
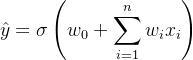

![打卡信奥刷题(2877)用C++实现信奥题 P5054 [COCI 2017/2018 #7] Dostavljač-网硕互联帮助中心](https://www.wsisp.com/helps/wp-content/uploads/2026/02/20260227052520-69a12ac0df0af-220x150.png)


评论前必须登录!
注册