一、算法简介
我们在刷题时总会遇到当答案过大时会要求对一个数取模,通常这个数为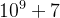 。我们在数论中可以得知边乘法边取模是成立的,而在除法中是不成立的。乘法逆元就是解决此类问题。
。我们在数论中可以得知边乘法边取模是成立的,而在除法中是不成立的。乘法逆元就是解决此类问题。
二、核心思想
对于取模运算有两个通用结论:
1.(a±b)%p=(a%p±b%p)%p
2.(a·b)%p=((a%p)·(b%p))%p
这两个结论使我们运算时能边加边取模或者边乘边取模。而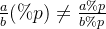 意味着我们不能边除边取模。那么我们考虑能否找到一个数
意味着我们不能边除边取模。那么我们考虑能否找到一个数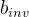 ,使得乘以这个数再取模后的结果等于除以一个数取模后的结果,即满足
,使得乘以这个数再取模后的结果等于除以一个数取模后的结果,即满足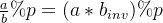 ,我们称
,我们称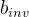 为
为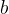 的乘法逆元。
的乘法逆元。
我们设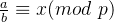 ,且存在
,且存在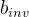 满足
满足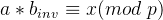 。将这两个式子两边同时乘以
。将这两个式子两边同时乘以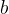 得到:
得到: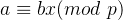 以及
以及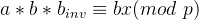 。将这两个式子相减得到:
。将这两个式子相减得到: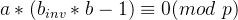 。其中
。其中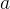 为任意数,如果想要让这个式子恒成立,
为任意数,如果想要让这个式子恒成立,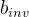 应满足
应满足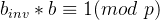 且此时为
且此时为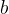 在模
在模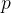 意义下的乘法逆元。格外注意:乘法逆元当且仅当
意义下的乘法逆元。格外注意:乘法逆元当且仅当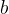 和
和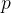 互质时候存在。题目常给的
互质时候存在。题目常给的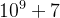 恰好为质数,且一般
恰好为质数,且一般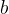 不会大于它,能够使我们进行逆元运算。
不会大于它,能够使我们进行逆元运算。
我们如何在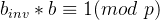 求得逆元呢?考虑费马小定理:若
求得逆元呢?考虑费马小定理:若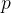 为质数,则
为质数,则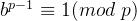 。观察两个式子的形式不难发现,只需取
。观察两个式子的形式不难发现,只需取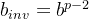 即可。至此我们求得了
即可。至此我们求得了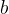 在模
在模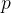 意义下的乘法逆元
意义下的乘法逆元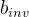 。
。
三、算法实现
由于需要计算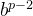 且通常
且通常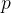 很大,因此需要使用快速幂算法,详见跳转我的另一篇文章: 快速幂速通(附代码)-CSDN博客
很大,因此需要使用快速幂算法,详见跳转我的另一篇文章: 快速幂速通(附代码)-CSDN博客
代码以求阶乘的逆元为例pr[i]表示i的阶乘在模p意义下的逆元。例如ans=(ans*pr[4])%p,等同于ans=(ans/pre[4])%p。从不能边除边模转化为可以边乘边模。
#include<cstdio>
#include<algorithm>
#include<cmath>
#define LL long long
using namespace std;
LL pre[1000002],pr[1000002],p=1e9+7;
LL ksm(LL a,LL b)
{
LL ans=1;//累乘操作初始为1
while(b)
{
if(b&1) ans=(ans*a)%p;//二进制处理,当指数为奇数时答案乘以底数
b>>=1;//二进制处理除以二
a=(a*a)%p;//底数平方
}
return ans;
}
LL inv(LL k)
{
return ksm(k,p-2);
}
int main()
{
LL i,n,j;
scanf("%lld",&n);
pre[0]=pr[1]=1;
for(i=1;i<=n;i++) pre[i]=(pre[i-1]*i)%p;
for(i=2;i<=n;i++) pr[i]=inv(pre[i]);
return 0;
}
码字不易,你的关注和点赞就是对我最大的支持!!
 网硕互联帮助中心
网硕互联帮助中心



评论前必须登录!
注册