《Matlab教学建模方法与实践（第三章）》学习笔记——主成分分析法(PCA)

目录

一、主成分分析(PCA)基本原理

1. PCA基本思想

2.PCA方法步骤

二、PCA应用案例

三、运用PCA的数模论文

一、主成分分析(PCA)基本原理

1. PCA基本思想

主成分分析是采用一种数学降维的方法，其所做的就是设法将原来众多具有一定相关性的变量，重新组合为一组新的综合变量来代替原来的变量。通常数学上的处理方法是将原来的变量做线性组合，作为新的综合变量，如果选取第一个线性组合即第一个综合变量为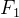。用方差测量新综合变量反应原来变量的信息，即希望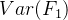越大，表示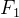包含的信息越多。因此在所有线性组合中，所选取的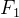应该使方差最大的，故称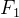为第一主成分。如果第一主成分不足以代表原来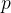个变量的信息，再考虑选取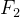，即第二个线性组合。为了有效地反应原来的信息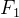，已有的信息就不需要再出现在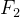中，用数学语言表示就是要求，称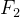为第二主成分。以此类推，可以构造出第三、第四、…、第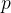个主成分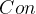（表示统计学中的协方差）

2.PCA方法步骤

• Step1：对原始数据进行标准化处理。假设样本观测数据矩阵为：

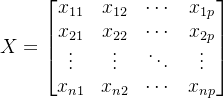
那么可以按照如下方法对原始数据进行标准化处理：

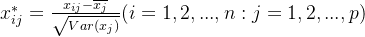
其中，

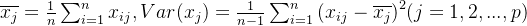
• Step2：计算样本相关系数矩阵，假设数据标准化后依旧用X表示，经过标准化处理后端数据的相关系数为：

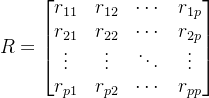
其中，

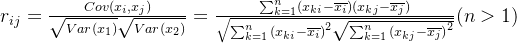
对于协方差，样本方差为，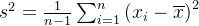

样本X和样本Y的协方差为

协方差为正时，说明X和Y是正相关关系；协方差为负时，说明X和Y是负相关关系；协方差为0时，说明X和Y是相互独立。Cov(X,X)就是X的方差。

• 计算相关系数矩阵R的特征值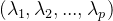和相应的特征向量：

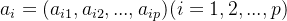
• 选择最主要的主成分，并写出主成分表达式。根据个个主成分累计贡献率的大小选取前k给主成分。贡献率是指主成分的方差占全部方差的比重，实际就是某个特征值占全部特征值合计的比重。

贡献率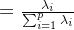

贡献率越大说明该主成分所包含的原始变量的信息越强。主成分个数k的选取，主要根据主成分的累计贡献率来决定，即一般要求累计贡献率达到85%以上，这样才能保证综合变量能包含原始变量的绝大多数信息。

• 计算主成分得分。根据标准化的原始数据，按照各个样品分别代入主成分表达式，得到个主成分下各个样品的新数据，即主成分得分。

其中，

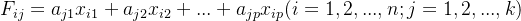
• 依据主成分得分的数据，进一步对问题进行后续的分析和建模。

二、PCA应用案例

为系统分析某IT企业的经济效益，选择了8个不同的利润指标，对15家企业进行调研，得到如下数据。请根据这些数据对15家企业进行综合实力排序。

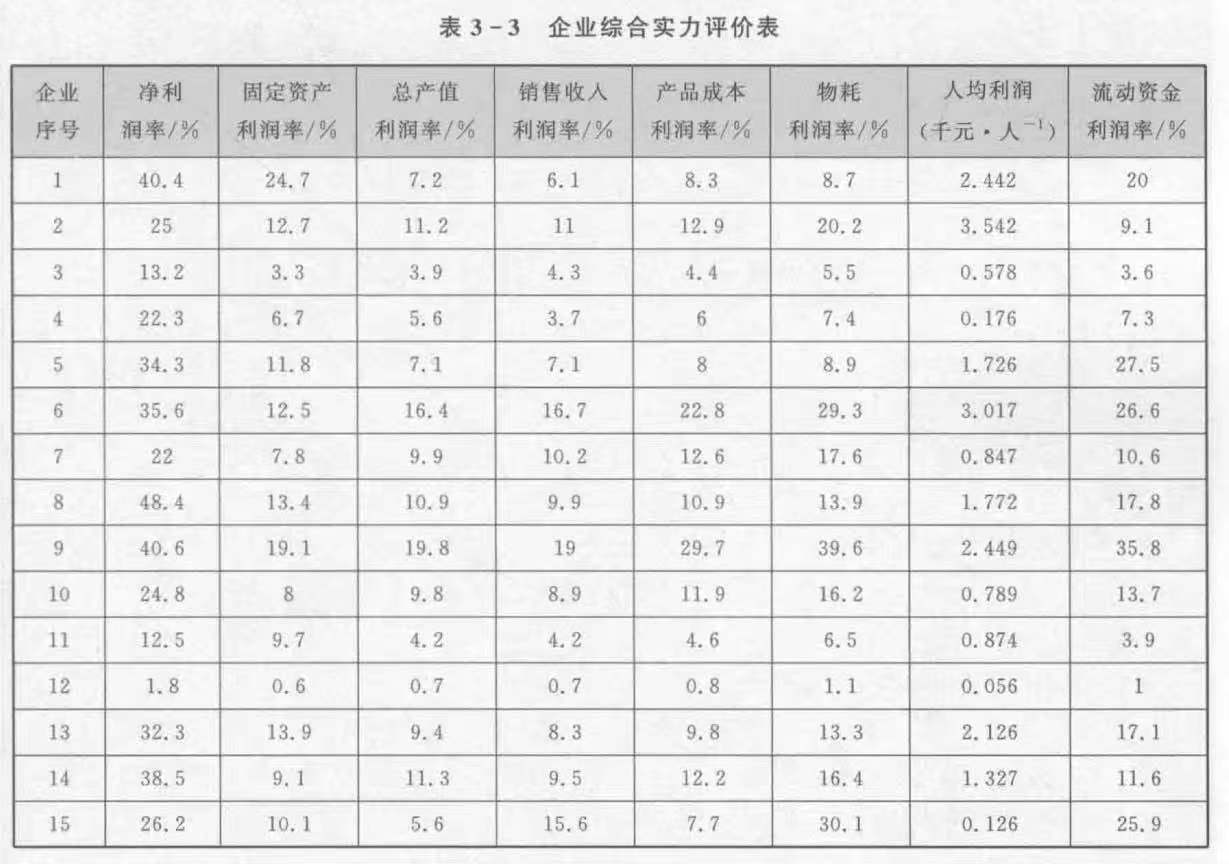
• 数据导入及处理

clc
clear all
A=xlsread('Coporation_evaluation.xlsx','B2:I16');

• 数据标准化处理

a=size(A,1);
b=size(A,2);
for i=1:b
SA(:,i)=(A(:,i)-mean(A(:,i)))/std(A(:,i));
end

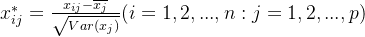
size()函数：获取矩阵的行数与列数。该代码把矩阵A的行数赋值给a，列数赋值给b，用于循环进行数据标准化。

①s=size(A)

当只有一个输出参数时，返回一个行向量，该行向量的第一个元素时矩阵的行数，第二个元素是矩阵的列数。

②[r,c]=size(A)

当有两个输出参数时，将矩阵的行数返回到第一个输出变量r，将矩阵的列数返回到第二个输出变量c。

③size(A,n)

如果在size函数的输入参数中再添加一项n，并用1或2为n赋值，则 size将返回矩阵的行数或列数。

r=size(A,1)该语句返回矩阵A的行数

r=size(A,2) 该语句返回矩阵A的列数

mean()函数：计算样本均值

①M = mean(A)

当只有一个输出参数时，返回 A 沿大小不等于 1 的第一个数组维度的元素的均值。

如果 A 是向量，则 mean(A) 返回元素均值。

如果 A 为矩阵，那么 mean(A) 返回包含每列均值的行向量。

②M = mean(A,‘all’)

当第二个参数是'all'时，返回 A 的所有元素的均值。

③M = mean(A,dim)

返回维度 dim 上的均值。

例如：a=[1,2,3;4,5,6;7,8,9];

• mean(a,1)

        ans =

        4 5 6

• mean(a,2)

        ans =

        2         5         8

• mean(a,3)

        ans =         1 2 3         4 5 6         7 8 9

std()函数：计算标准差

①S = std(A)，返回 A 沿大小不等于 1 的第一个数组维度的元素的标准差。

②S = std(A,w)

当 w = 0 时（默认值），S 按 N-1 进行归一化。

当 w = 1 时，S 按观测值数量 N 进行归一化。

③S = std(A,w,dim)，沿维度 dim 返回标准差。

• 计算相关系数矩阵的特征值和特征函数

CM=corrcoef(SA);%计算相关系数矩阵
[V,D]=eig(CM);%计算特征值和特征向量
for j=1:b
DS(j:1)=D(b+1-j,b+1-j);%对特征值按降序排列
end
for i=1:b
DS(i,2)=DS(i,1)/sum(DS(:,1))；%贡献率
DS(i,3)=sum(DS(1:i,1))/sum(DS(:,1));%累计贡献率

corrcoef()函数：计算相关系数矩阵

eig()函数：计算矩阵的特征值和特征向量

• 选择主成分及其对应的特征向量

T=0.9;
for K=1:b
if DS(K,3)>T
Com_num=K;
break;
end
end

• 提取主成分对应的特征向量

for j=1:Con_num
PV(:,j)=V(:,b+1-j);
end

• 计算各评价对象的主成分得分

new_score=SA*PV
for i=1:a
total_score(i,1)=sum(new_score(i,:));
total_score(i,2)=i;
end
result_report=[new_score,total_score];%将各主成分得分与总分放在同一个矩阵
result_report=sortrows(result_report,-4);%将总分按照降序排列

sortrows()函数：排序

①B = sortrows(A)

默认依据第一列的数值按升序排序。

②B = sortrows(A,column)

从某一列开始比较数值并进行排序。

如果column>0则升序排列

如果column<0则降序排列

③[B,index] = sortrows(A,…)

B返回排序后的矩阵，index返回排序后的行索引

• 输出模型及报告结果

disp('特征值及其贡献率、累计贡献率:')
DS
disp('信息保留率T对应的主城分数与特征向量:')
Com_num
PV
disp('主成分得分及排序（按第四列的总分进行降序排序，前三列为各主成分得分，第五列为企业编号）:')
result_report

三、运用PCA的数模论文