【算法】图的 深度优先搜索(DFS)与 广度优先搜索(BFS)
在图中,我们可能会按一些顺序遍历整个图,例如从一个节点到另一个节点的最短路径,或者判断节点是否联通,都可以使用这两种搜索方法
1. 深度优先搜索(DFS)
深度优先搜索(Depth-First Search,DFS),简称深搜,它的原则是从一个点开始,向与这个点之间联通的另一条边出发,再从另一条点出发,除了原来那个点,继续去找点,知道自己已经没有可以找的点了,就退回去,以它的上一个点再来找另一个点,再来重新出发,返回,出发,返回……最终所有路径遍历完以后,就遍历完毕了
这么一说可能有一些抽象,所以接下来会用一些图片进行演示
例如我们从 节点 111 开始,搜索所有节点,问节点的 DFS 序
DFS 序:从某个节点开始搜索,搜索到每个节点的顺序
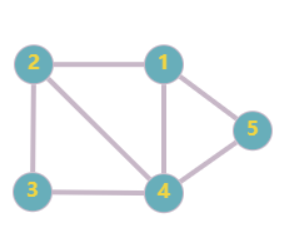
从节点 111 开始,按照顺序先遍历节点 222 (这里以遍历节点 222 开始,实际上也可以先遍历节点 444 或节点 555,不考虑顺序,所以答案不唯一,但是后面作者都会按照节点编号选择)
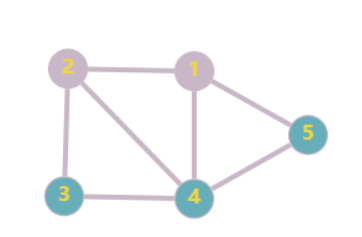
随后遍历到节点 222 后,又去找与它相连的点,虽然节点 111 和它相连,但是它被遍历过,所以选择 333 号
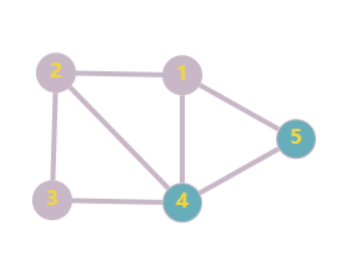
然后,继续找 444 和 555,最终,得出顺序:1→2→3→4→51 \\rightarrow 2 \\rightarrow 3 \\rightarrow 4 \\rightarrow 51→2→3→4→5
但是,程序中一般不会看 DFS 序,而是 DFS 遍历,在 555 号遍历完后还没有遍历完,回溯到 444,看还有没有另外的路径,没有又回溯到 333 ,回溯到 222,222 还连着 444,因此又从 444 开始。往做走,走到了 333,然后没有路走了。因此第二条路就是 1→2→4→31\\rightarrow2\\rightarrow4\\rightarrow31→2→4→3,回溯到 444,又找到了一条路
因此,程序遍历的话会遍历出这么多路径
1 -> 2 -> 3 -> 4 -> 5
1 -> 2 -> 4 -> 3
1 -> 2 -> 4 -> 5
1 -> 4 -> 2 -> 3
1 -> 4 -> 3 -> 2
1 -> 4 -> 5
1 -> 5 -> 4 -> 2 -> 3
1 -> 5 -> 4 -> 3 -> 2
不过因为按照编号,所以顺序拥有字典序
那么代码中又应该怎么写呢?
众所周知,深度优先搜索因为从某节点进入,又从某节点回溯,而且都是在调用的地方中执行,这是栈的结构,一提到栈,我们不难想到函数的递归操作,每回只操作当前节点,操作完后去操作上一个节点
这里的程序会先输入两个数字 nnn 、mmm 和 kkk ,表示点数(节点编号从 111 到 nnn)、边数与起点,随后输入 mmm 行,每行两个数字 uuu 和 vvv,表示 uuu 和 vvv 连接了一条无向边。输出所有路径,中间用 -> 连接起来
1≤n,m≤10001\\leq n, m \\leq 10001≤n,m≤1000
1≤u,v≤n1 \\leq u, v \\leq n1≤u,v≤n
例如将上面那一张图转换为输入信息(从节点 111 开始)
5 7 1
1 2
1 4
1 5
2 3
2 4
3 4
4 5
#include <bits/stdc++.h>
using namespace std;
vector<int> G[1005]; // 邻接表
bool Vis[1005]; // 是否遍历了当前节点,防止重复遍历
void Dfs (int cur, string pth) {
bool flag = 1; // 是否显示路径(是否遍历到头了)
for (int i : G[cur]) { // 遍历与它相连的点
if (Vis[i]) continue; // 防止重复遍历
flag = 0; // 取消标记
Vis[i] = 1; // 标记遍历
Dfs(i, pth + " -> " + to_string(i)); // 递归继续遍历
Vis[i] = 0; // 取消标记(这是易错点)
}
if (flag) cout << pth << '\\n'; // 输出路径
}
int main () {
// 输入
int n, m, k, u, v;
cin >> n >> m >> k;
while (m—) {
cin >> u >> v;
G[u].push_back(v);
G[v].push_back(u);
}
for (int i = 1; i <= n; i++) sort(G[i].begin(), G[i].end()); // 输出排列有字典序
Vis[k] = 1; // 标记开头(这是易错点)
Dfs(k, to_string(k)); // 开始深搜
return 0;
}
2. 广度优先搜索(BFS)
广度优先搜索或宽度优先搜索(BFS,Breadth-First Search),简称广搜或宽搜。这个东西从一个点开始,不断地向外面层层扩散,一层,二层,三层……这样,我们也很容易找到从一个地方到另一个地方的最短路径,这也是一种遍历图的方法
例如下面这张图(黑色是障碍,蓝色是维护的队列元素,红色是遍历过的,绿色是起点,粉色是终点)
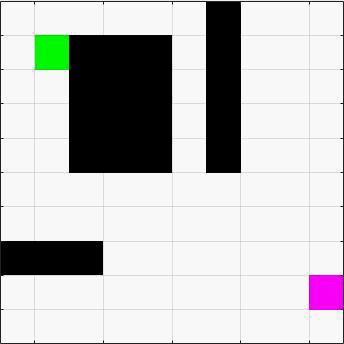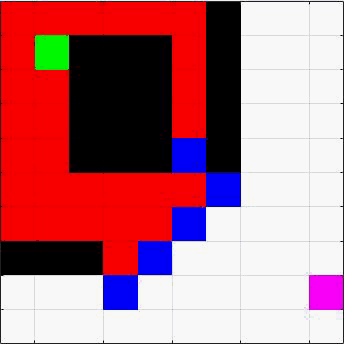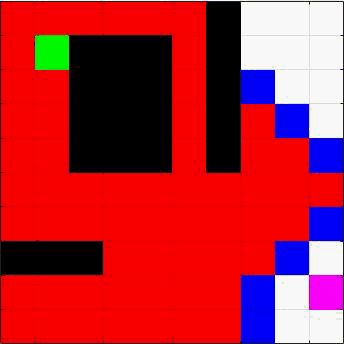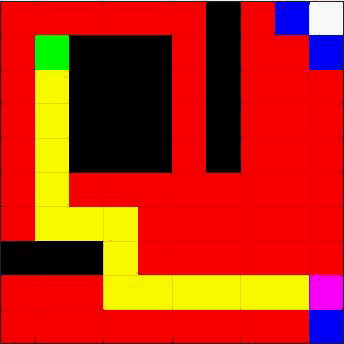
构建一个队列,里面初始放着起始节点。队列会让它不断找到新的节点,随后节点消失,从扩散的节点继续走。这样就能让路径不断扩散,找到路径
DFS 可以递归也可以维护一个栈,但 BFS 只能维护一个队列操作,由于它分层扩散,所以找到的路也是最短的路径
例如这个问题。有一个 n×nn \\times nn×n 的迷宫,迷宫中有些位置存在障碍物,111 表示障碍物,000 表示空地。已知某一个人处于迷宫的 (a,b)(a,b)(a,b) 位置,迷宫的出口在 (c,d)(c,d)(c,d) 位置,问东东是否可以从迷宫中走出去,如果可以,输出最少移动步数,如果不可以,输出 −1-1−1
第一行输入两个正整数 n(1≤n≤100)n(1 \\le n \\le 100)n(1≤n≤100),表示迷宫的大小
后面 nnn 行每行 nnn 个整数描述这个迷宫,111 表示障碍物,000 表示空地
最后一行 444 个正整数 a,b,c,da,b,c,da,b,c,d 分别表示东东的位置和迷宫的出口,数据保证这两个位置是空地
如果可以走出迷宫,输出最少步数,否则输出 −1-1−1
输入:
4
0 0 0 0
1 1 0 1
0 0 0 1
0 0 1 0
1 1 3 3
输出:
4
#include <bits/stdc++.h>
using namespace std;
struct Pos { // 位置结构体
int x, y, t; // t 是从 (sx,sy) 到 (x,y) 的最短路径
};
// 四联通数组
const int dx[4] = {0, 1, 0, –1};
const int dy[4] = {1, 0, –1, 0};
int n;
int sx, sy, ex, ey;
int x, y, t, tx, ty;
bool A[120][120]; // 迷宫
queue<Pos> Q; // 维护的队列
int bfs () {
Q.push({sx, sy, 0});
A[sx][sy] = 1;
while (Q.size()) {
// 当前路径
x = Q.front().x;
y = Q.front().y;
t = Q.front().t;
if (x == ex && y == ey) return t; // 到达终点(绝对最短路)
Q.pop(); // 注意删除防止重复调用
for (int i = 0; i < 4; i++) { // 四联通
// 下一次会移动到哪里
tx = x + dx[i];
ty = y + dy[i];
if (tx >= 1 && tx <= n && ty >= 1 && ty <= n && !A[tx][ty]) { // 防止走出头了
A[tx][ty] = 1; // 这里因为只找最短路,之前的迷宫可以想象为走一步就不能回头了,路被堵住了
Q.push({tx, ty, t + 1}); // 向外拓展
}
}
}
return –1; // 找不到路径
}
int main () {
// 输入
cin >> n;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
cin >> A[i][j];
cin >> sx >> sy >> ex >> ey;
// 输出
cout << bfs();
return 0;
}
 网硕互联帮助中心
网硕互联帮助中心


评论前必须登录!
注册