数组中的第K个最大元素

题目：

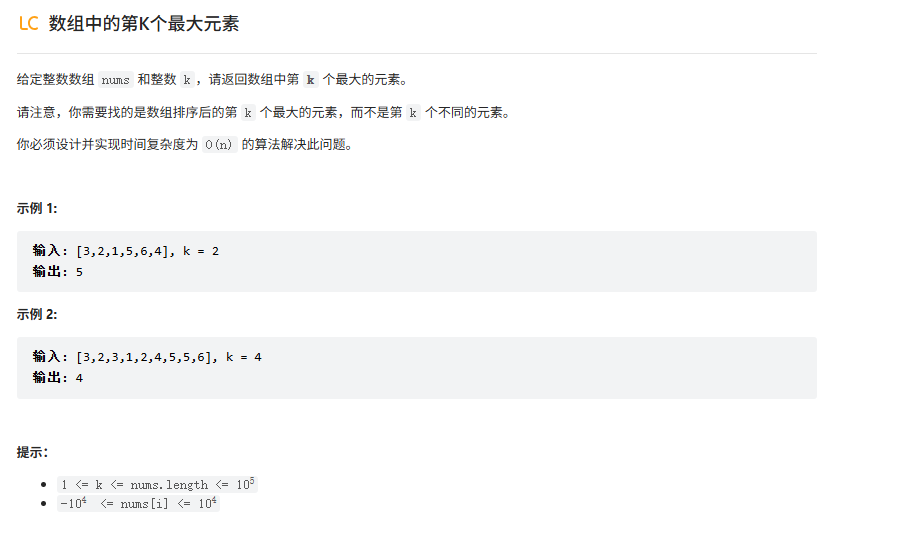
思考1：

实现采用小根堆方法：

class Solution {
public:
void adjust(vector<int>& heap,int t)
{
int max=t;

while(2*max+1<heap.size())
{
int l=2*max+1;
int r=2*max+2;

if (r<heap.size())
{
if (heap[l]<heap[r])
{
if (heap[l]<heap[max])
{
swap(heap[l],heap[max]);
max=l;
}
else
{
break;
}
}
else
{
if (heap[r]<heap[max])
{
swap(heap[r],heap[max]);
max=r;
}
else
{
break;
}
}
}
else
{
if (heap[l]<heap[max])
{
swap(heap[l],heap[max]);
max=l;
}
else
{
break;
}
}
}
}
int findKthLargest(vector<int>& nums, int k) {
vector<int> heap(nums.begin(),nums.begin()+k);

int max=k/2–1;

for (int i=max;i>=0;—i)
{
adjust(heap,i);
}

for (int i=k;i<nums.size();i++)
{
if (nums[i]>heap[0])
{
heap[0]=nums[i];
adjust(heap,0);
}
}

return heap[0];
}
};

思考二:

实现：

class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
return quickSelect(nums, 0, nums.size() – 1, k);
}

private:
int quickSelect(vector<int>& nums, int left, int right, int k) {
if (left == right) return nums[left];

int pivotIndex = left + rand() % (right – left + 1);
int pivot = nums[pivotIndex];

int i = left, j = right, p = left;
while (p <= j) {
if (nums[p] > pivot) {
swap(nums[p], nums[i]);
i++;
p++;
} else if (nums[p] < pivot) {
swap(nums[p], nums[j]);
j—;
} else {
p++;
}
}

int bigCount = i – left;

int equalCount = j – i + 1;

if (k <= bigCount) {
return quickSelect(nums, left, i – 1, k);
} else if (k <= bigCount + equalCount) {
return pivot;
} else {
return quickSelect(nums, j + 1, right, k – bigCount – equalCount);
}
}
};