算法学习第三天 【快速排序】

快速排序

三路快排：原理介绍（高效处理重复数据）

在学习快速排序的分区（partition）操作前，我们可以思考这样一个问题：

给定一个数组：[2, 7, 6, 1, 4, 5, 2, 3]
我们希望选择一个基准值（pivot），比如选最右边的元素 3，然后对数组进行重新排列，使得：

• 所有 小于 3 的元素放在数组的左边；
• 所有 等于 3 的元素放在中间；
• 所有 大于 3 的元素放在右边。

这种划分方式称为 三路划分（3-way partitioning），特别适合处理包含大量重复元素的数组。

为了实现这一目标，我们可以使用 三个指针（或区间边界） 来维护三个区域：

• lt：指向“小于区”的右边界（即小于 pivot 的最后一个位置）
• gt：指向“大于区”的左边界（即大于 pivot 的第一个位置）
• i：当前遍历指针，从左到右扫描数组

初始时：

• lt = -1（表示小于区为空）
• gt = n（即 gt = 8，表示大于区从索引 8 开始，也为空）
• i = 0（从第一个元素开始遍历）

我们以 pivot = 3 为例，开始遍历（i < gt 时继续）：

遍历规则如下：

举例说明：

初始数组：[2, 7, 6, 1, 4, 5, 2, 3]，pivot = 3

经过三路划分后，数组可能变成类似： [2, 1, 2, 3, 7, 6, 5, 4]
（前面是 <3 的，中间是 =3 的，后面是 >3 的）

最终，lt 和 gt 之间的元素就是所有等于 pivot 的值，可用于后续递归处理左右两部分。

我们刚才完成的操作，称为 分区（Partition）。
它的核心作用是：给定一个数组和一个基准值（pivot），通过重新排列，将数组划分为三个连续的区域：

• 左侧：所有 小于 pivot 的元素
• 中间：所有 等于 pivot 的元素
• 右侧：所有 大于 pivot 的元素

这一过程完成后，中间区域（即所有等于 pivot 的元素）就已经处于最终排序位置，无需再次调整。我们只需递归地对左侧的“小于区”和右侧的“大于区”重复相同的分区操作，就能逐步使整个数组有序。

试想，如果我们对左边的“小于区”也选择一个新的基准值，进行同样的三路分区；
同时对右边的“大于区”也如此处理；
那么每一层操作都在将问题分解为更小的子问题。
随着递归不断深入，子数组的规模逐渐缩小，直到某个子数组长度为 0 或 1 —— 此时已自然有序。

当所有递归调用逐层返回时，整个数组也就完成了排序。

代码实现

#include <stdio.h>

void swap(int *a, int *b)
{
int temp = *a;
*a = *b;
*b = temp;
}

void quickSort(int *nums, int low, int high)
{
if (low >= high)
return;

int pivot = nums[low];
int lt = low;
int gt = high;
int i = low + 1;

while (i <= gt){
if (nums[i] < pivot){
swap(&nums[lt], &nums[i]);
lt++;
i++;
}
else if (nums[i] > pivot){
swap(&nums[gt], &nums[i]);
gt–;
// 这里 i 不增加，因为还没有比较换过来的数的大小
}
else{
i++;
}
}

quickSort(nums, low, lt – 1);
quickSort(nums, gt + 1, high);
}

int main()
{
int nums[] = {4,3,2,2,5,6,7,5,3,3,2,1,4};
int len = sizeof(nums) / sizeof(int);

// 快速排序
quickSort(nums, 0, len – 1);

// 打印输出
for (int i = 0; i < len; i++){
printf("%d ", nums[i]);
}
return 0;
}

双边扫描快排：原理介绍（通用简洁写法）

这是一种通用、直观、广泛流传的快速排序实现，适合大多数情况。虽然在大量重复元素下不如三路快排高效，但代码简洁，易于理解和教学。

选择最左侧元素作为 pivot，使用两个指针 left 和 right 从数组两端向中间扫描：

• right 从右向左找第一个小于 pivot 的元素
• left 从左向右找第一个大于 pivot 的元素
• 找到后交换两者位置
• 直到 left >= right

循环结束后，left（或 right）指向的位置就是 pivot 的最终位置。将 nums[left] 与 nums[low]（原始 pivot）交换，完成分区。

随后递归处理 left 左右两个子数组。

代码实现

#include <stdio.h>

void swap(int *a, int *b)
{
int temp = *a;
*a = *b;
*b = temp;
}

void quickSort(int *nums, int low, int high)
{
if (low >= high)
return;

int pivot = nums[low];
int left = low;
int right = high;

while (left < right){
while (left < right && nums[right] >= pivot)
right–;

while (left < right && nums[left] <= pivot)
left++;

if (left < right)
swap(&nums[left], &nums[right]);
}

swap(&nums[left], &nums[low]);
quickSort(nums, low, left – 1);
quickSort(nums, left + 1, high);
}

int main()
{
int nums[] = {2, 7, 6, 1, 4, 5, 2, 3};
int len = sizeof(nums) / sizeof(int);

// 快速排序
quickSort(nums, 0, len – 1);

for (int i = 0; i < len; i++)
printf("%d ", nums[i]);

return 0;
}

两种实现快排方法的对比

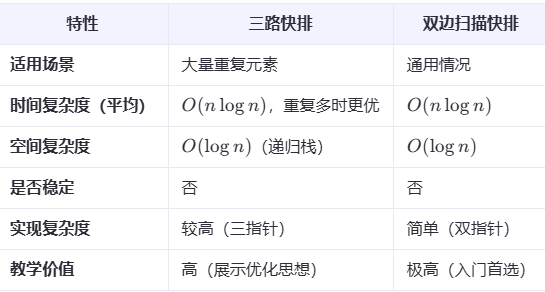
优化方案

前面介绍的两种快排写法，基准值都是固定选的（比如选第一个或最后一个元素）。这种做法在大多数情况下效率很高，但如果遇到已经有序或者特定排列的数据，每次划分都极不均衡，就会导致性能急剧下降，最坏时间复杂度退化到 O(n²)。

为了避免这种情况，我们可以改进基准值的选择方式，让算法更“聪明”、更稳定。常用的优化方法有：

• 三数取中：取数组的第一个、中间的和最后一个元素，选其中的中位数作为基准，避免极端情况。
• 随机选基准：随机从数组中选一个元素作为基准，用随机性来对抗坏数据。