一、Scikit-Learn机器学习概述
Scikit-Learn(sklearn)是Python最常用的机器学习库,特点包括:
核心设计思想:将机器学习流程标准化为"数据输入 → 特征处理 → 模型训练 → 预测输出"的流水线
二、KNN算法(K最近邻分类)
1. 样本距离判断
KNN的核心是计算样本间的距离,常用方法:
-
欧氏距离(直线距离):
( d = \\sqrt{\\sum_{i=1}^{n}(x_i – y_i)^2} )
例如:点A(1,2)和点B(4,6)的距离 = (\\sqrt{(1-4)^2 + (2-6)^2} = 5) -
曼哈顿距离(城市街区距离):
( d = \\sum_{i=1}^{n}|x_i – y_i| )
同上例:|1-4| + |2-6| = 3 + 4 = 7
2. 算法原理
核心思想:“物以类聚”——未知样本的类别由其k个最近邻居的多数投票决定
工作流程:
3. 关键参数与缺点
- k值选择:
- k太小 → 对噪声敏感(过拟合)
- k太大 → 忽略局部特征(欠拟合)
- 缺点:
- 计算效率低(高时间复杂度):KNN需要计算测试样本与所有训练样本的距离(如欧氏距离),时间复杂度为 O(n)(n为训练样本数)。当数据量很大时,预测速度极慢。
- 存储空间需求大:KNN是“惰性学习”(Lazy Learning),训练阶段仅存储数据,不生成显式模型。因此,预测时需保留全部训练数据,空间复杂度为 O(n)。
- 对高维数据敏感(维度灾难):在高维空间中,样本间距离差异变小(所有点趋于等距),导致KNN难以找到真正相似的邻居。
- 不平衡数据的分类偏差:若各类别样本数量差异大,KNN可能偏向多数类,忽略少数类。【解决方法:加权投票(根据距离赋予不同权重),采样平衡数据(过采样少数类或欠采样多数类)】
- 参数K的选择敏感:K值(邻居数量)对结果影响显著:
K过小:模型对噪声敏感,容易过拟合(如K=1时,预测仅依赖最近一个样本)。
K过大:模型可能忽略局部结构,导致欠拟合(如K=训练集大小时,预测结果恒为多数类)。【解决方法:通过交叉验证选择最优K,但增加计算成本】 - 对噪声和异常值敏感:KNN的预测基于局部邻居,若邻居中包含噪声或异常值,结果会被干扰。【缓解方法:数据清洗(去除异常值),使用加权KNN(距离越近的邻居权重越高)】
4. sklearn API
from sklearn.neighbors import KNeighborsClassifier
model = KNeighborsClassifier(n_neighbors=5, metric='euclidean') # metric可选'manhattan'
5. 实战示例:鸢尾花分类
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
# 加载数据
iris = load_iris()
X, y = iris.data, iris.target
# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
# 训练模型
model = KNeighborsClassifier(n_neighbors=3)
model.fit(X_train, y_train)
# 评估准确率
accuracy = model.score(X_test, y_test) # 输出如0.95
6. 模型保存与加载
import joblib
# 保存模型
joblib.dump(model, 'knn_model.pkl')
# 加载模型
loaded_model = joblib.load('knn_model.pkl')
三、模型选择与调优
1. 为什么需要调优?
- 问题:传统训练/测试集划分可能导致数据利用不充分或评估偏差(如随机划分时测试集恰好包含简单样本)。
- 目标:通过多次划分数据,更可靠地估计模型在未见数据上的泛化能力。
2. 交叉验证(Cross-Validation)
解决的问题:单次数据划分可能引入随机偏差
(1)K折交叉验证流程(K-Fold CV)
(以5折为例):
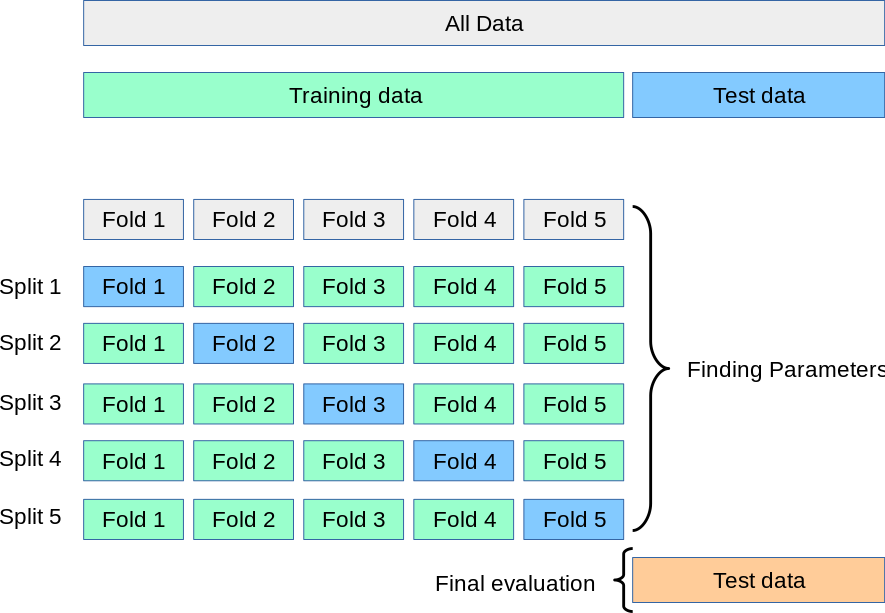
优点:
- 数据利用率高(每个样本均参与验证)。
- 减少因单次划分导致的评估波动。
缺点:计算成本随K增加而上升(K通常取5或10)。
(2)留一法交叉验证(LOOCV)
- 步骤:K折CV的特例,K=样本数,每次仅留1个样本验证。
- 优点:偏差极低(几乎用全部数据训练)。
- 缺点:计算量极大(尤其大数据集)。
(3)分层K折交叉验证(Stratified K-Fold)
- 适用场景:分类任务中类别不平衡时。
- 改进:确保每折中各类别比例与原始数据集一致,避免因划分导致验证集类别分布失真。
3. 超参数搜索
- 网格搜索(Grid Search):遍历所有可能的参数组合
- 随机搜索(Random Search):随机抽样参数组合(效率更高)
4. sklearn API
class sklearn.model_selection.GridSearchCV(estimator, param_grid)
说明:
同时进行交叉验证(CV)、和网格搜索(GridSearch),GridSearchCV实际上也是一个估计器(estimator),同时它有几个重要属性:
best_params_ 最佳参数
best_score_ 在训练集中的准确率
best_estimator_ 最佳估计器
cv_results_ 交叉验证过程描述
best_index_最佳k在列表中的下标
参数:
estimator: scikit–learn估计器实例
param_grid:以参数名称(str)作为键,将参数设置列表尝试作为值的字典
示例: {"n_neighbors": [1, 3, 5, 7, 9, 11]}
cv: 确定交叉验证切分策略,值为:
(1)None 默认5折
(2)integer 设置多少折
如果估计器是分类器,使用"分层k-折交叉验证(StratifiedKFold)"。在所有其他情况下,使用KFold。
5. 示例:鸢尾花分类调优
# 用KNN算法对鸢尾花进行分类,添加网格搜索和交叉验证
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import GridSearchCV
def knn_iris_gscv():
# 1)获取数据
iris = load_iris()
# 2)划分数据集
x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=22)
# 3)特征工程:标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
# 4)KNN算法预估器, 这里就不传参数n_neighbors了,交给GridSearchCV来传递
estimator = KNeighborsClassifier()
# 加入网格搜索与交叉验证, GridSearchCV会让k分别等于1,2,5,7,9,11进行网格搜索偿试。cv=10表示进行10次交叉验证
estimator = GridSearchCV(estimator, param_grid={"n_neighbors": [1, 3, 5, 7, 9, 11]}, cv=10)
estimator.fit(x_train, y_train)
# 5)模型评估
# 方法1:直接比对真实值和预测值
y_predict = estimator.predict(x_test)
print("y_predict:\\n", y_predict)
print("直接比对真实值和预测值:\\n", y_test == y_predict)
# 方法2:计算准确率
score = estimator.score(x_test, y_test)
print("在测试集中的准确率为:\\n", score) #0.9736842105263158
# 最佳参数:best_params_
print("最佳参数:\\n", estimator.best_params_) #{'n_neighbors': 3}, 说明k=3时最好
# 最佳结果:best_score_
print("在训练集中的准确率:\\n", estimator.best_score_) #0.9553030303030303
# 最佳估计器:best_estimator_
print("最佳估计器:\\n", estimator.best_estimator_) # KNeighborsClassifier(n_neighbors=3)
# 交叉验证结果:cv_results_
print("交叉验证过程描述:\\n", estimator.cv_results_)
#最佳参数组合的索引:最佳k在列表中的下标
print("最佳参数组合的索引:\\n",estimator.best_index_)
#通常情况下,直接使用best_params_更为方便
return None
knn_iris_gscv()
四、朴素贝叶斯分类
1. 算法基础
- 条件概率:事件A在事件B已发生时的概率 ( P(A|B) = \\frac{P(A \\cap B)}{P(B)} )
- 全概率公式:若事件B由互斥事件( A_1,…,A_n )引发,则
( P(B) = \\sum_{i=1}^{n} P(B|A_i)P(A_i) )
2. 贝叶斯定理
( P(A|B) = \\frac{P(B|A)P(A)}{P(B)} )
其中:
- ( P(A|B) ):后验概率(我们要求解的)
- ( P(B|A) ):似然概率
- ( P(A) ):先验概率
3. 朴素贝叶斯原理
"朴素"假设:特征之间相互独立(简化计算)
分类决策:计算样本属于各类别的概率,取最大值
( P(y_k|x) = \\frac{P(x|y_k)P(y_k)}{P(x)} \\propto P(y_k) \\prod_{i} P(x_i|y_k) )
4. 拉普拉斯平滑
问题:当某个特征值未出现时,( P(x_i|y_k)=0 )导致整体概率为0
解决方案:添加平滑系数α (如α = 1)
( P(x_i|y_k) = \\frac{N_{y_k,x_i} + \\alpha}{N_{y_k} + \\alpha n} )
其中:
- ( N_{y_k,x_i} ):类别( y_k )中特征( x_i )出现的次数
- ( N_{y_k} ):类别( y_k )的总样本数
- ( n ):特征的可能取值数
5. sklearn API
from sklearn.naive_bayes import MultinomialNB # 适用于离散特征
model = MultinomialNB(alpha=1.0) # alpha即平滑系数
6. 示例:新闻分类
from sklearn.datasets import fetch_20newsgroups
from sklearn.feature_extraction.text import CountVectorizer
# 加载数据
newsgroups = fetch_20newsgroups(subset='train')
X, y = newsgroups.data, newsgroups.target
# 文本特征提取
vectorizer = CountVectorizer()
X_vec = vectorizer.fit_transform(X)
# 训练朴素贝叶斯
model = MultinomialNB(alpha=0.01)
model.fit(X_vec, y)
# 预测新文本
new_text = ["GPU performance comparison"]
new_vec = vectorizer.transform(new_text)
pred = model.predict(new_vec) # 输出类别编号
关键知识点总结
| KNN | 小数据集,低维度 | 直观易理解 | 计算效率低,需特征缩放 |
| 朴素贝叶斯 | 文本分类,高维度 | 计算高效,抗噪声 | 特征独立性假设可能不成立 |
| 模型调优 | 所有算法 | 显著提升模型性能 | 计算成本高 |
 网硕互联帮助中心
网硕互联帮助中心



评论前必须登录!
注册