数学家、图灵机、计算理论、计算机、程序设计语言和编译器

Hilbert -> Turing -> Chomsky -> …

1. 希尔伯特的23个问题（1900年）

1900年，德国数学家大卫·希尔伯特（David Hilbert）在巴黎国际数学家大会上提出了23个未解决的数学问题，这些问题深刻影响了20世纪数学的发展方向。这些问题涵盖广泛领域，包括数论、代数、几何、分析、逻辑等，其中一些问题至今仍未完全解决，而另一些则催生了新的数学分支（如计算理论、拓扑学、数理逻辑等）。现分类与概述23个问题。

1.1. 数学基础（逻辑与公理化）

问题1：连续统假设（CH）

康托尔提出：是否存在一个基数严格介于可数无穷（ℵ₀）和实数集基数（ℵ₁）之间的集合？

现状：哥德尔（1940）和科恩（1963）证明，CH在ZFC公理系统内既不能被证明也不能被证伪（独立于ZFC）。

问题2：算术公理的一致性

希尔伯特希望证明数学公理系统（如算术）不会导致矛盾。

现状：哥德尔不完备性定理（1931）证明，任何足够强的公理系统无法自证一致性，图灵机的停机问题进一步强化了这一结论。

问题10：判定丢番图方程的可解性

问题：是否存在通用算法判定任意整系数多项式方程是否有整数解？

现状：1970年，马蒂亚谢维奇（基于图灵机理论）证明不存在这样的算法（希尔伯特第十问题不可解）。

1.2. 代数与数论

问题3：两个等体积多面体的剖分相等性

问题：给定两个体积相同的多面体，能否通过有限切割重组使它们全等？

现状：德恩（1900）给出反例，表明不一定成立。

问题7：某些数的超越性（如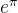 $e^\\pi$ ）

问题：证明某些数（如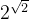 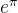$2^{\\sqrt{2}}$ 、 $e^\\pi$ ）是超越数。

现状：格尔丰德-施奈德定理（1934）部分解决，但仍有开放问题。

问题9：任意数域中的互反律推广

问题：推广高斯二次互反律到更一般的数域。

现状：阿廷（1927）提出类域论，部分解决。

问题11：二次型理论

问题：研究代数数域上的二次型理论。

现状：哈塞（1920s）等有重要贡献，但仍有许多开放问题。

问题12：阿贝尔域的克罗内克定理推广

问题：推广克罗内克的“青春之梦”猜想到更一般的域。

现状：类域论部分解决，但完整推广仍未完成。

1.3. 几何与拓扑

问题4：构造所有度量几何的公理系统

问题：研究不同几何（欧氏、非欧、射影等）的公理化。

现状：拓扑学和微分几何的发展部分解决。

问题5：李群的拓扑性质

问题：研究连续变换群（李群）是否总是可微？

现状：1952年，格里森等证明局部欧氏群必为李群（希尔伯特第五问题解决）。

问题6：物理学的公理化

问题：为物理学（特别是概率论和力学）建立严格的数学基础。

现状：量子力学、统计力学等发展部分解决。

问题15：代数几何的舒伯特计数演算严格化

问题：严格化舒伯特的“枚举几何”方法。

现状：20世纪代数几何（格罗滕迪克等）发展后基本解决。

问题18：空间填充问题（密铺理论）

问题：研究高维空间的最密堆积（如球体堆积）。

现状：开普勒猜想（三维球堆积，1998年证明），但更高维仍未完全解决。

1.4. 分析与方程

问题8：素数分布（黎曼猜想、哥德巴赫猜想等）

问题：研究素数分布（如黎曼ζ函数的零点）。

现状：黎曼猜想（未解决），哥德巴赫猜想（陈景润部分证明）。

问题13：七次方程的解（一般七次方程是否可用有限超椭圆函数表示）

问题：推广椭圆函数理论到更高次方程。

现状：部分解决（阿贝尔积分、代数几何）。

问题16：代数曲线与曲面的拓扑

问题：研究代数曲线/曲面的极限环（如希尔伯特第16问题）。

现状：动力系统研究仍在进行，部分解决。

问题19：变分法的解析解

问题：研究拉格朗日方程的解是否总是解析的。

现状：伯恩斯坦等有部分结果，但仍有开放问题。

问题20：偏微分方程边值问题的解

问题：研究物理方程（如热方程、波动方程）的解的存在性。

现状：泛函分析、索伯列夫空间等理论部分解决。

问题21：具有给定单值群的线性微分方程

问题：研究微分方程的单值群（Monodromy）问题。

现状：代数几何和微分方程理论部分解决。

问题22：解析关系的单值化

问题：研究多值函数（如复变函数）的单值表示。

现状：单值化定理（庞加莱、克贝等）部分解决。

1.5. 数学物理

问题23：变分法的进一步发展

问题：研究变分法在物理中的应用（如最小作用量原理）。

现状：现代物理（量子场论、弦论）仍在发展相关数学。

1.6. 情况总结

已解决：问题3、5、10、15、17、18（部分）、21、22等。

部分解决：问题1、2、7、8、9、11、16、19、20等。

未解决：黎曼猜想（问题8之一）、哥德巴赫猜想（问题8之二）、希尔伯特第16问题的完整解等。

希尔伯特的23个问题塑造了现代数学的格局，推动了数理逻辑、计算理论、代数几何、拓扑学等领域的革命性发展。

2. 希尔伯特23问题与图灵机的关系

2.1. 与图灵机相关的希尔伯特问题

以下问题与计算理论和图灵机有直接或间接关联：

第1问题（连续统假设）
康托尔的连续统假设（CH）探讨无穷集合的基数问题。图灵机在可计算性理论中的研究（如停机问题）揭示了数学中某些命题的不可判定性，这与哥德尔不完备定理共同说明CH在ZFC公理体系内无法被证明或证伪。

第2问题（算术公理的无矛盾性）
希尔伯特希望证明数学系统的一致性。但哥德尔不完备定理（1931年）和图灵的工作表明，任何足够强的公理系统（如算术）无法自证其一致性。图灵机的停机问题正是这种不可判定性的体现。

第10问题（丢番图方程的可解性）
问题：是否存在通用算法判定整系数多项式方程是否有整数解？

1970年，马蒂亚谢维奇（Yuri Matiyasevich）基于图灵机、递归函数理论证明不存在这样的算法，即希尔伯特第十问题不可解。

2.2. 图灵机与希尔伯特纲领的关联

希尔伯特的形式主义纲领试图将数学建立在有限步骤的机械证明（即“能行性”）基础上。图灵机的提出（1936年）为此提供了理论模型：

可计算性：图灵机形式化了“算法”概念，证明某些问题（如停机问题）无法通过算法解决。

不完备性：结合哥德尔定理，图灵机表明希尔伯特寻求的“完备且一致的数学系统”不可能存在。

2.3. 影响与意义

图灵机为计算机科学奠定基础，希尔伯特问题中的逻辑与可计算性研究直接催生了现代计算理论(计算理论诞生)。通过图灵机，人们认识到数学中存在本质上不可判定的问题（如停机问题、某些数论问题），这重塑了数学哲学（数学的边界）。

2.4. 未解问题与延伸

部分希尔伯特问题（如黎曼猜想，第8问题之一）仍待解决，而图灵机的概念被用于研究这些问题的可计算性。例如：是否存在图灵机可判定的步骤验证黎曼猜想的所有非平凡零点？

2.5. 问题小结

希尔伯特的第1、2、10问题与图灵机深刻相关，揭示了数学的可计算边界和形式化极限。图灵机不仅是计算机的理论基石，也终结了希尔伯特关于“数学完全形式化”的梦想，转而开辟了可计算性理论的新领域。

3. 乔姆斯基（Noam Chomsky）与图灵机和计算理论

历史到了乔姆斯基时代。

乔姆斯基（1928—）是美国著名语言学家、哲学家、认知科学家，同时也是计算理论的重要奠基人之一。他的形式语言理论与图灵机、自动机理论、程序设计语言、编译器等领域密切相关，直接影响计算机科学的发展。

3.1. 乔姆斯基与形式语言（乔姆斯基谱系）

乔姆斯基在1956年提出形式语言的分类（即乔姆斯基谱系），将语言分为4个层次，对应不同的自动机模型和计算能力：

语言类型文法规则自动机模型计算能力程序设计语言例子

0型（递归可枚举语言）	无限制文法	图灵机	可计算问题（停机问题不可解）	理论上可描述所有计算
1型（上下文相关语言）	上下文相关文法	线性有界自动机（LBA）	比图灵机弱，但比下推自动机强	XML、自然语言处理
2型（上下文无关语言）	上下文无关文法（CFG）	下推自动机（PDA）	可被栈式机器解析	大多数编程语言（C、Python）
3型（正则语言）	正则文法	有限状态自动机（FA）	最简单的模式匹配	正则表达式（a*b）

Chomsky 的关键贡献在于证明了不同文法对应不同计算模型，为编译器设计提供理论基础。例如，上下文无关文法（CFG）是编程语言语法分析（如BNF范式）的核心。

3.2. 乔姆斯基与图灵机的关系

图灵机（1936）是最通用的计算模型，可计算所有递归可枚举语言（乔姆斯基0型语言）。

乔姆斯基谱系揭示了图灵完备性，即任何0型语言均可由图灵机处理（如现代编程语言）；也揭示了计算限制：

1型语言（LBA）比图灵机弱，但仍能处理复杂模式（如自然语言）。

2型语言（PDA）对应编程语言的语法解析（如编译器前端）。

3型语言（FA）用于词法分析（如正则表达式匹配）。

3.3. 乔姆斯基与自动机理论

乔姆斯基的形式语言分类直接对应自动机层级：

自动机计算能力应用

有限状态自动机（FA）	正则语言（3型）	词法分析（Lex）、正则表达式
下推自动机（PDA）	上下文无关语言（2型）	语法分析（Yacc、LR解析）
线性有界自动机（LBA）	上下文相关语言（1型）	复杂模式识别（自然语言处理）
图灵机	递归可枚举语言（0型）	通用计算（编程语言、算法）

关键影响：

词法分析（Lexer）：使用有限状态自动机（如Flex）。

语法分析（Parser）：使用下推自动机（如Bison、ANTLR）。

编译器设计：乔姆斯基体系指导了编译原理的分层处理（词法→语法→语义）。

3.4. 乔姆斯基与程序设计语言

现代编程语言的设计深受乔姆斯基理论影响。语法规则的定义，会使用乔姆斯基的理论。例如，大多数语言（C、Java、Python）使用上下文无关文法（CFG）定义语法。例如，BNF（巴科斯范式）用于描述编程语言的语法规则：

<if-statement> ::= "if" "(" <condition> ")" <statement>

这同时影响了编译器前端的实现，例如词法分析（正则表达式→有限自动机）和语法分析（CFG→下推自动机）的实现。

3.5. 乔姆斯基与编译器

可以直言，乔姆斯基的理论是编译器整体构造的核心：

词法分析（Lexical Analysis）

使用正则表达式（3型语言）定义Token（如if, while, 123）。

由有限状态自动机（FA）实现（如Flex工具）。

语法分析（Syntax Analysis）

使用上下文无关文法（2型语言）构建抽象语法树（AST）。

由下推自动机（PDA）实现（如Bison、LR解析器）。

语义分析与代码生成

更复杂的语言特性（如类型检查）可能涉及上下文相关（1型）甚至递归可枚举（0型）问题。

3.6. 乔姆斯基对计算理论的深远影响

乔姆斯基对计算复杂性工作影响深远。乔姆斯基谱系与P vs NP问题相关（正则语言∈P，上下文无关语言∈P，但某些0型语言不可判定）。

乔姆斯基的生成语法理论影响计算机语言学。编程语言设计：几乎所有现代语言（C、Java、Python）的语法都基于上下文无关文法（CFG）。

3.7. 问题总结

乔姆斯基的形式语言理论与自动机分类工作，奠定了编译原理的基础（词法分析→语法分析→代码生成）。连接了图灵机、自动机与编程语言，揭示计算能力的层次结构。直接影响编译器设计（如Lex/Yacc、ANTLR等工具）。他的工作不仅是理论计算机科学的基石，也直接塑造了现代编程语言和编译器技术。

4. 图灵机（Turing Machine, TM）详解

图灵机是计算机科学的理论计算模型，由阿兰·图灵（Alan Turing）于1936年提出。它定义了“可计算性”的数学边界，并成为现代计算机的理论基础。

4.1. 图灵机的定义

图灵机是一个抽象的数学计算设备，由以下组件构成：

无限长的纸带（Tape）：
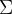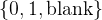被划分为离散的格子，每个格子可存储一个符号（来自有限字母表 $\\Sigma$ ，如 $\\{0, 1, \\text{blank}\\}$ ）。

读写头（Head）：
可以读取当前格子的符号，并根据规则写入新符号、左移（L）或右移（R）。

状态寄存器（State Register）：
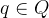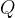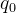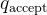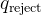保存当前状态 $q \\in Q$ （为有限状态集），包括一个特殊的起始状态 q_0 和若干终止状态（如接受状态 $q_{\\text{accept}}$ 和拒绝状态 $q_{\\text{reject}}$ ）。

转移函数（Transition Function）：
决定机器的行为，形式为：

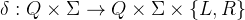
$\\delta: Q \\times \\Sigma \\rightarrow Q \\times \\Sigma \\times \\{L, R\\}$
含义：若当前状态为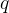，读到的符号为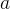，则转移到状态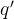，写入符号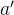，并移动读写头。

4.2. 图灵机的工作流程

初始化：

纸带输入字符串（如 101），其余格子为空白。

读写头指向最左端符号，状态设为 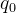q_0 。

逐步执行：

根据当前状态和读到的符号，查找转移函数 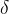$\\delta$ 并执行对应操作。

重复直到进入终止状态。

终止：

若进入 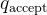$q_{\\text{accept}}$ ，输出“接受”；

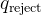若进入 $q_{\\text{reject}}$ ，输出“拒绝”；

若永不停止（如无限循环），则问题“不可计算”。

示例：判断二进制数是否为偶数（最低位为0）

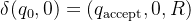
$\\delta(q_0, 0) = (q_{\\text{accept}}, 0, R)$

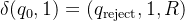
$\\delta(q_0, 1) = (q_{\\text{reject}}, 1, R)$

4.3. 图灵机的关键性质

4.3.1. 计算通用性

丘奇-图灵论题（Church-Turing Thesis）：
任何可计算问题均可由图灵机解决。虽无法严格证明，但被广泛接受。

等价模型：
图灵机与λ演算、递归函数、现代计算机（冯·诺依曼架构）在计算能力上等价。

4.3.2. 可计算性分类

可判定问题（Decidable）, 存在图灵机在有限步内总能给出答案（如“一个数是否为素数”）。

不可判定问题（Undecidable）, 例如停机问题（Halting Problem）：无法设计一个图灵机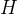，判断任意程序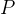在输入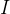下是否会停止。

4.3.3. 复杂度类别

P类问题, 图灵机在多项式时间内可解（如排序）。

NP类问题, 图灵机在多项式时间内可验证解（如数独）。

NP完全问题, NP中最难的问题（如旅行商问题），若任一NP完全问题被证明属于P，则P=NP。

4.4. 图灵机的变体与扩展

4.4.1. 非确定性图灵机（NTM）

允许转移函数有多个可能动作，机器“猜测”正确路径。

与确定性图灵机（DTM）等价，但时间复杂度不同（NP问题在NTM上可多项式时间求解）。

4.4.2. 多带图灵机

使用多条纸带，读写头独立移动。等价于单带图灵机，但可提升时间效率（如时间 O(n) 变为 $O(n/\\log n)$ ）。

4.4.3. 量子图灵机（QTM）

纸带和状态为量子比特，转移函数为幺正算子。可解决经典TM难解问题（如Shor算法），计算复杂度类为 BQP。

4.5. 图灵机的功能示例

4.5.1 算术运算

加法：输入 #a#b#（a, ba,b 为二进制数），通过状态转移逐位计算并处理进位。

乘法：需更复杂的状态设计，利用多带图灵机优化。

4.5.2 语言识别

判定回文（Palindrome）, 检查输入字符串是否正反相同（如 madam）。
步骤：

step1. 复制输入到第二条纸带。

step2. 反转第二条纸带。

step3. 逐字符比较。

4.5.3 模拟算法

通用图灵机（UTM）：
可模拟任何其他图灵机，原理类似现代计算机的“程序存储”概念。
输入格式：<编码后的TM描述>#输入字符串#。

4.6. 图灵机的局限性

物理限制, 无限纸带无法真实实现，但可通过“外存扩展”近似（如硬盘）。

复杂度爆炸, 即使可计算的问题（如国际象棋），也可能因时间/空间复杂度过高而实际不可行。

4.7. 图灵机的意义

理论层面, 定义了计算的数学边界，为可计算性理论奠基。

工程层面, 冯·诺依曼架构的计算机是图灵机的物理实现。

哲学层面, 引发“机器能否思考”的讨论（图灵测试）。

4.8. 总结表：图灵机核心要点

组件描述示例

纸带	无限长，存储符号	…空白,0,1,1,空白,…
读写头	读取/写入符号并移动	当前指向第二个格子（符号 1）
状态寄存器	当前状态（如）	起始状态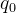
转移函数	规则表，决定下一步动作	$\\delta(q_0, 1) = (q_1, 0, R)$

4.9. 图灵机与计算机的对应关系

图灵机概念计算机实现

纸带	内存（RAM+硬盘）
读写头	CPU的指令指针（IP）
状态寄存器	CPU的当前程序状态（寄存器）
转移函数	机器指令集（如x86）

图灵机不仅是理论工具，更是理解计算本质的钥匙。