【数据结构初阶】-二叉树(四) - 网硕互联帮助中心

🔥个人主页：@草莓熊Lotso

🎬作者简介：C++研发方向学习者

📖个人专栏：《C语言》《数据结构与算法》《C语言刷题集》《Leetcode刷题指南》

⭐️人生格言：生活是默默的坚持，毅力是永久的享受。

前言：在前面我们结束了实现顺序结构的二叉树以及Top-K问题的解决。那么接下来就是实现链式结构二叉树，链接结构的二叉树，没有完全二叉树和堆那样的性质，所以我们后续实现的接口也不会涉及插入删除等操作，主要是前中后序遍历以及其它的一些二叉树常用方式的实现。

一.创建链式结构二叉树

二.前中后序遍历

前序遍历：

代码实现：

函数递归栈栈图：(标的序号表示打印的顺序)

前序遍历结果(忽略NULL)：

中序遍历：

代码实现：

函数栈帧递归图：(标的序号表示打印的顺序)

中序遍历结果(忽略NULL)：

后序遍历：

代码实现：

函数递归栈帧图： (标的序号表示打印的顺序)

后序遍历结果(忽略NULL)：

三.代码展现

Tree.h：

Tree.c：

test.c：

一.创建链式结构二叉树

–用链表来表示⼀棵二叉树，即用链来指示元素的逻辑关系。通常的方法是链表中每个结点由三个域组成，数据域和左右指针域，左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址，其结构如下：(我们数据类型这次用的char)

typedef char BTDataType;
typedef struct BinaryNode
{
BTDataType data;
struct BinaryNode* left;//左孩子
struct BinaryNode* right;//右孩子
}BTNode;

我们为了方便后续的使用，先手动创建一颗链式二叉树：

BTNode* buyNode(char x)
{
BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
newnode->data = x;
newnode->left = newnode->right = NULL;
return newnode;
}
void test1()
{
BTNode* nodeA = buyNode('A');
BTNode* nodeB = buyNode('B');
BTNode* nodeC = buyNode('C');
BTNode* nodeD = buyNode('D');
BTNode* nodeE = buyNode('E');
BTNode* nodeF = buyNode('F');

nodeA->left = nodeB;
nodeA->right = nodeC;
nodeB->left = nodeD;
nodeC->left = nodeE;
nodeC->right = nodeF;
}

创建出来的树如图所示：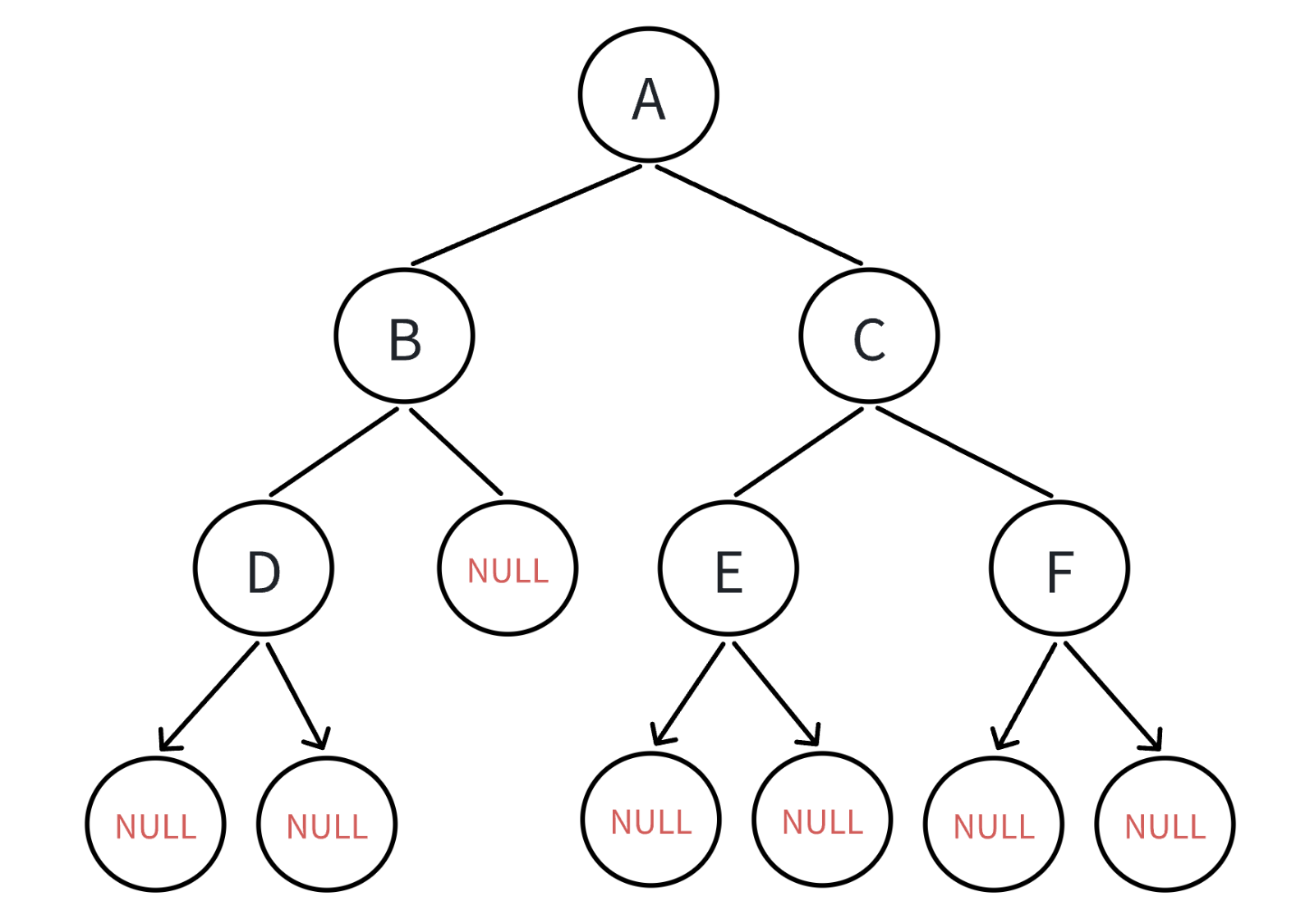

二.前中后序遍历

–二叉树的操作遍历是必不可少的，我们先来看看这些遍历的遍历规则吧

按照规则，二叉树的遍历有：前序/中序/后序的递归结构遍历：

前序遍历(先根遍历)：先遍历根节点，再遍历左子树，最后遍历右子树—-根左右
中序遍历：先遍历左子树，再遍历根节点，最后遍历右子树—-左根右
后续遍历：先遍历左子树，再遍历右子树，最后遍历根节点—-左右根

就拿我们创建的这个树为例，那么它的前中后遍历结果和代码实现是怎样的呢，我们一起接着往下看

前序遍历：

访问顺序：根节点，左子树，右子树

代码实现：

//前序遍历
void PreOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
//根左右
printf("%c ", root->data);
PreOrder(root->left);
PreOrder(root->right);
}

这份代码是不是看起来特别简单，这里就是利用了递归的思想，为空就打印NULL并返回。大家一定要去仔细体会一下递归的过程，最好把函数递归的栈帧图给画出来理解。大家可以先看一下我画的两个图。

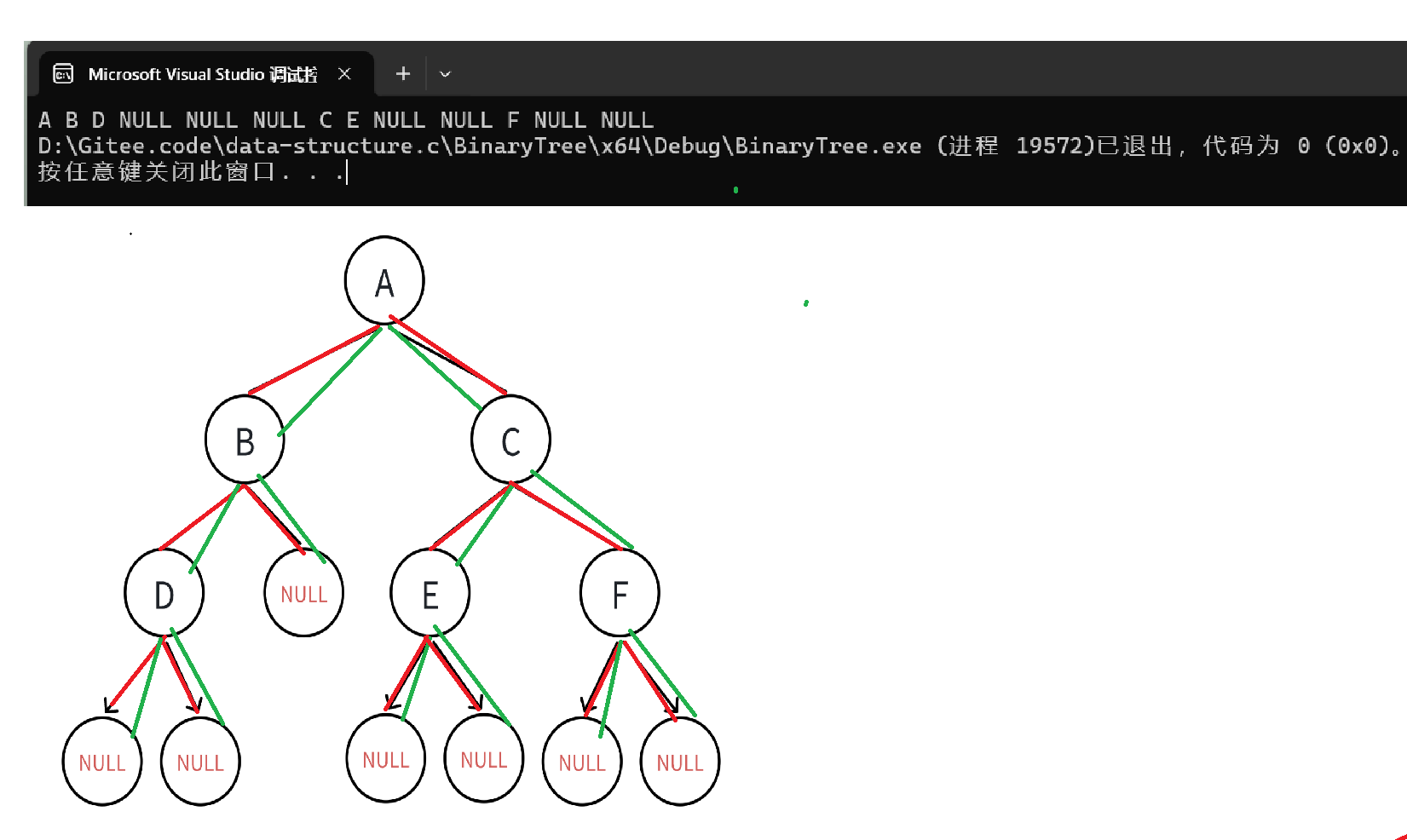这里红线统一表示递归，另一个表示回退

函数递归栈栈图：(标的序号表示打印的顺序)

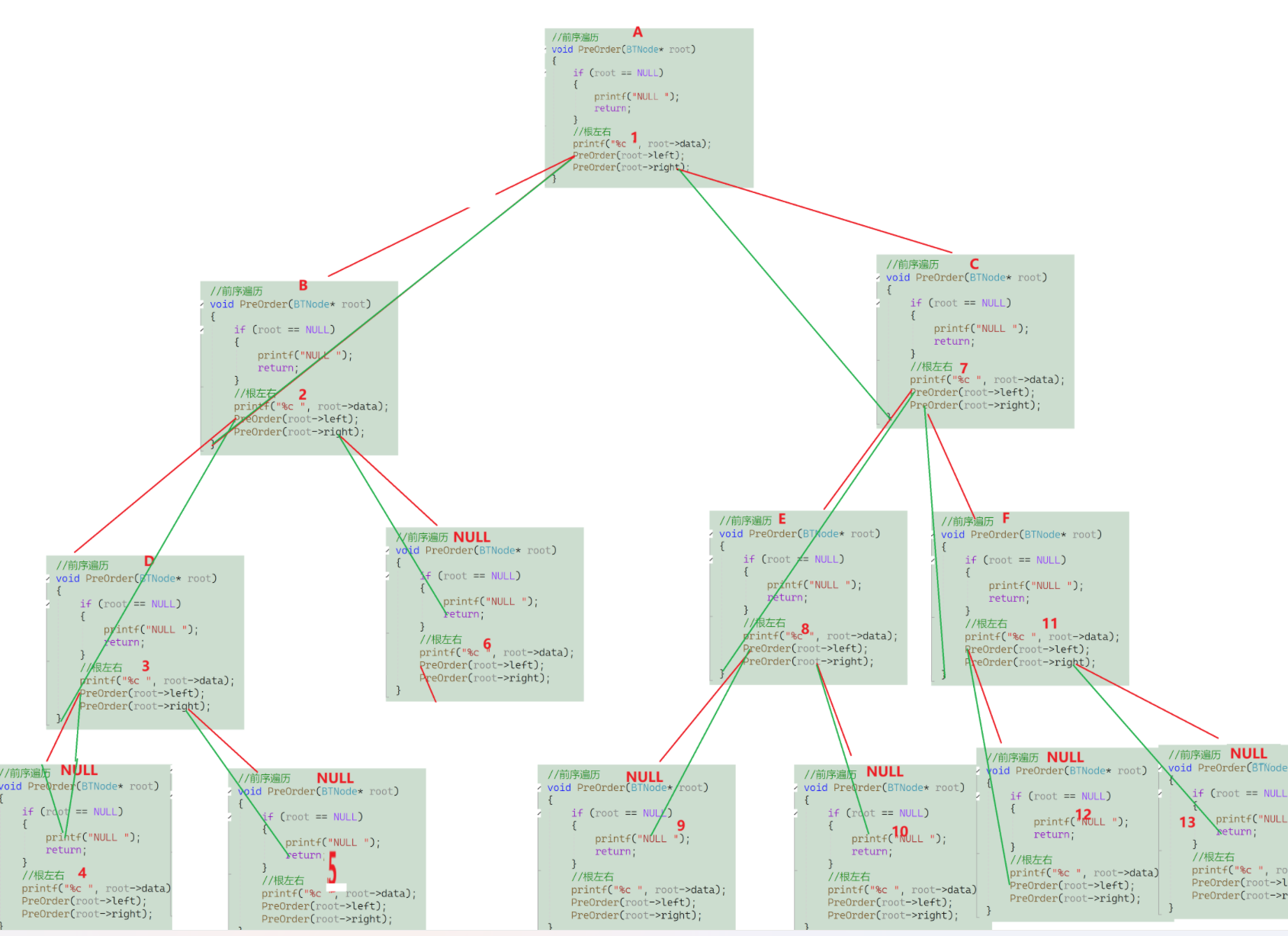
前序遍历结果(忽略NULL)：

A B D C E F

中序遍历：

访问顺序：左子树，根节点，右子树

代码实现：

//中序遍历
void InOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}

//左根右
InOrder(root->left);
printf("%c ", root->data);
InOrder(root->right);
}

这里的中序遍历代码也都很简单，注意顺序就好了。我们还是和上面的一样，通过画图理清它的递归逻辑

函数栈帧递归图：(标的序号表示打印的顺序)

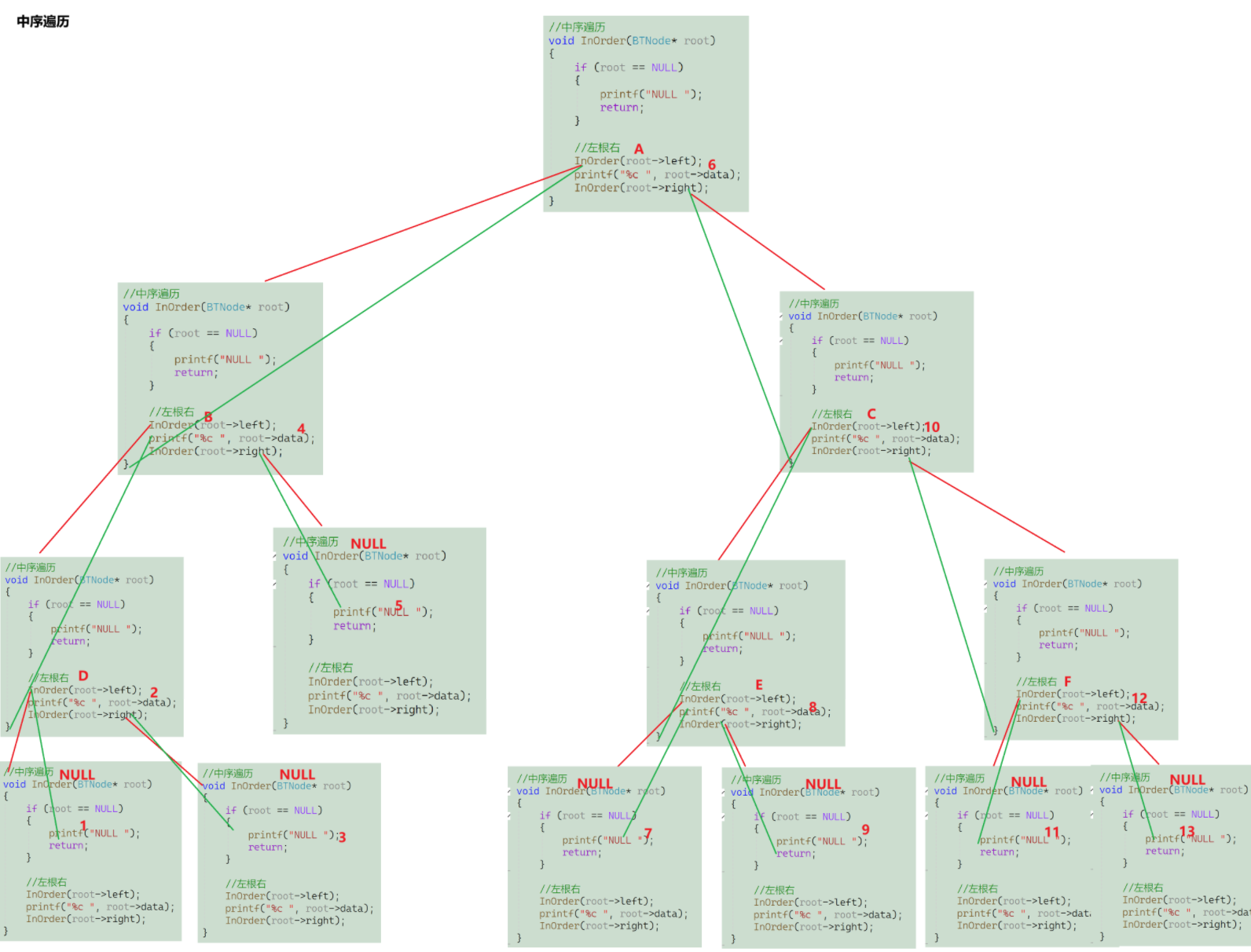
中序遍历结果(忽略NULL)：

D B A E C F

后序遍历：

访问顺序：左子树，右子树，根节点

代码实现：

//后续遍历
void PostOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}

//左右根
PostOrder(root->left);
PostOrder(root->right);
printf("%c ", root->data);
}

后序遍历的代码也很简单，和前面两种一样还是利用递归的思想去实现，我们继续通过画函数递归栈帧图来理清它的逻辑

函数递归栈帧图： (标的序号表示打印的顺序)

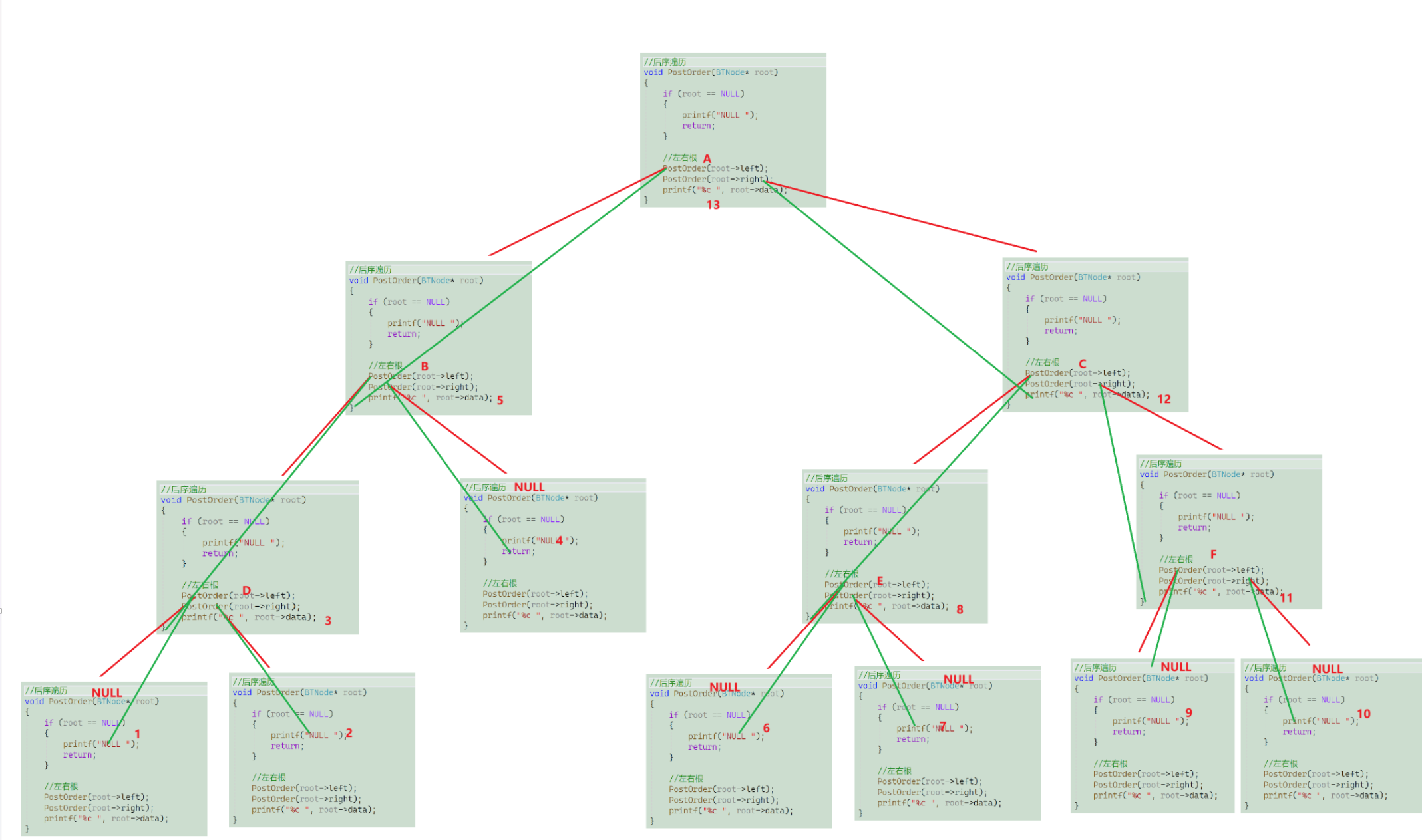
后序遍历结果(忽略NULL)：

D B E F C A

三.代码展现

Tree.h：

#pragma once
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>

typedef char BTDataType;
typedef struct BinaryNode
{
BTDataType data;
struct BinaryNode* left;//左孩子
struct BinaryNode* right;//右孩子
}BTNode;

//前序遍历
void PreOrder(BTNode* root);

//中序遍历
void InOrder(BTNode* root);

//后序遍历
void PostOrder(BTNode* root);

Tree.c：

#include"Tree.h"

//前序遍历
void PreOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
//根左右
printf("%c ", root->data);
PreOrder(root->left);
PreOrder(root->right);
}

//中序遍历
void InOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}

//左根右
InOrder(root->left);
printf("%c ", root->data);
InOrder(root->right);
}

//后序遍历
void PostOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}

//左右根
PostOrder(root->left);
PostOrder(root->right);
printf("%c ", root->data);
}

test.c：

#include"Tree.h"

nodeA->left = nodeB;
nodeA->right = nodeC;
nodeB->left = nodeD;
nodeC->left = nodeE;
nodeC->right = nodeF;

//PreOrder(nodeA);
//InOrder(nodeA);
PostOrder(nodeA);
}

int main()
{
test1();
return 0;
}

往期回顾：

【数据结构初阶】–栈和队列(二)

【数据结构初阶】–树和二叉树先导篇

【数据结构初阶】–二叉树(二)

【数据结构初阶】–二叉树(三)

结语：本篇博客中我们实现了二叉树的前中后序遍历以及画出了它们的函数递归栈帧图。大家还是需要多去熟悉一样，最好是理清它们的递归过程，后面我们会经常需要画函数递归栈帧图的。在下篇博客中我会和大家一起继续实现链式结构二叉树的其它方法接口，如果文章对你有帮助的话，欢迎评论，点赞，收藏加关注，感谢大家的支持。

【数据结构初阶】--二叉树(四)

一.创建链式结构二叉树