算法题（149）：矩阵消除游戏

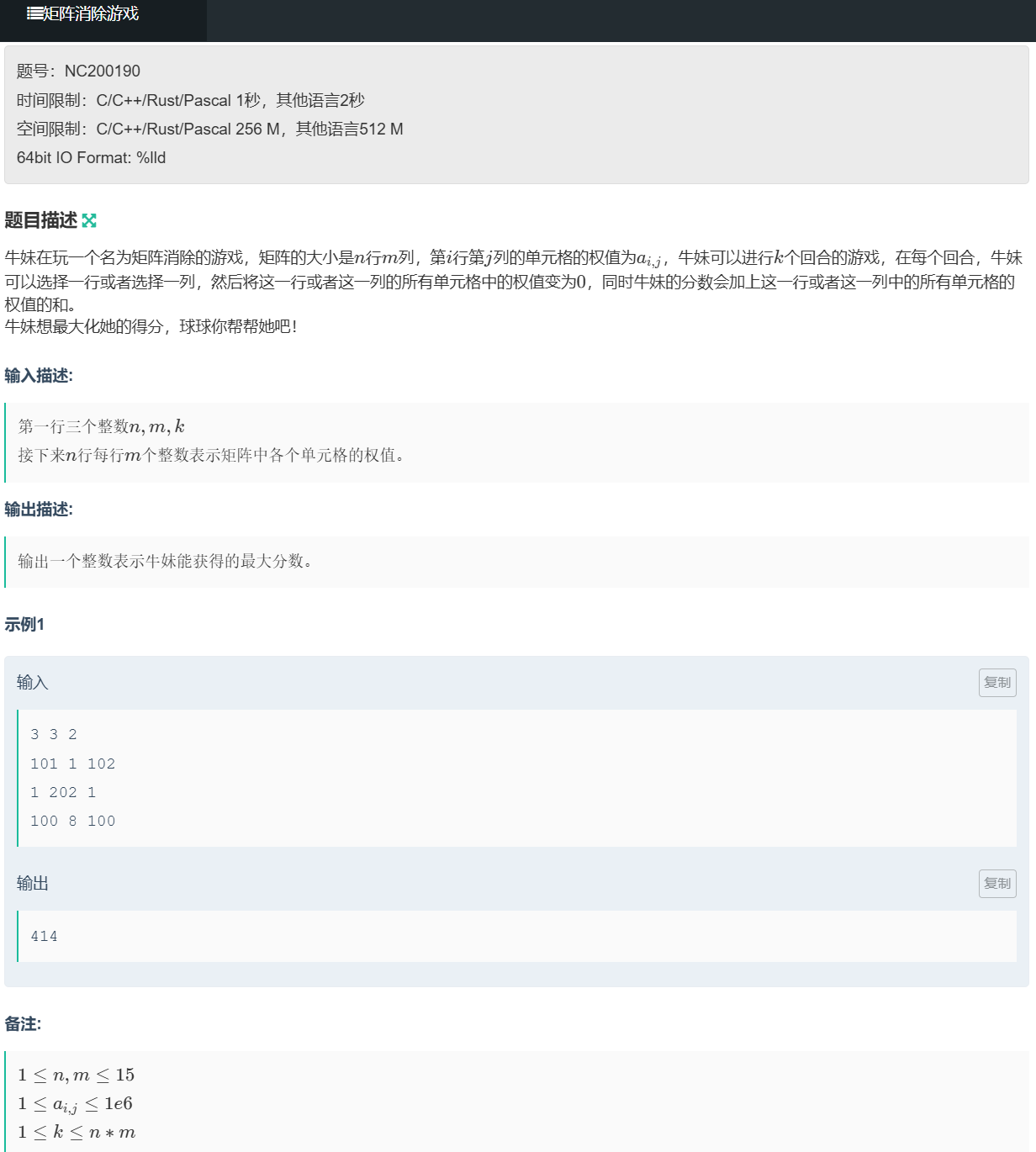
审题： 本题需要我们找到消除矩阵行与列后可以获得的最大权值

思路： 方法一：贪心+二进制枚举

这里的矩阵消除时，行与列的消除会互相影响，所以如果我们先统计所有行和列的总和，然后选择消除最大的那一行/列，选择完后更新所有行和列的总和，再循环进行消除选择，此时会导致部分情况无法得到最优解。

eg：进行回合数限制为2，矩阵如下图

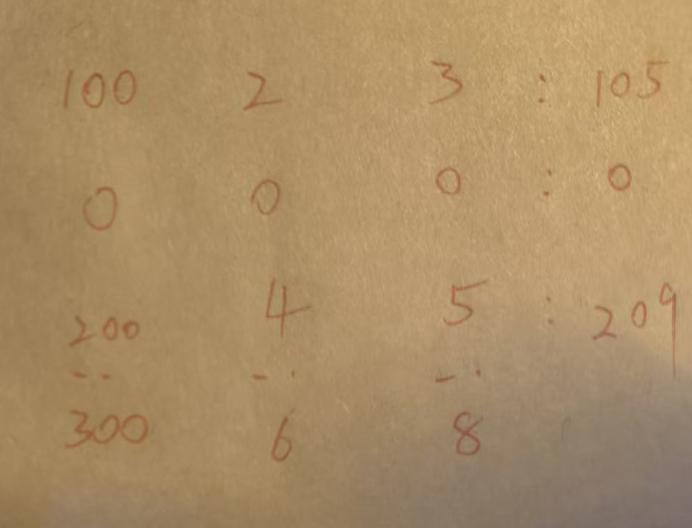
此时我们会先选择第一列，然后更新各行列的总和

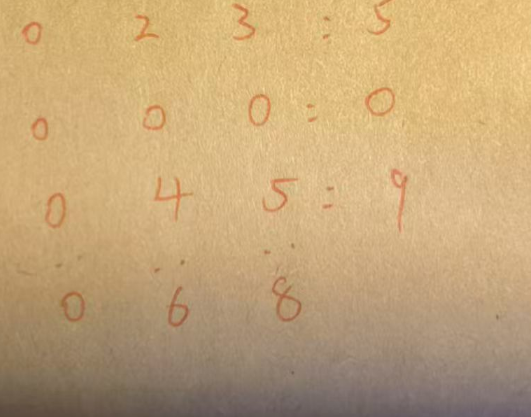
此时我们就再选择第三行，选择结束

不过其实我们完全一开始可以直接就选择第一行和第三行，这样子两个回合就拿到了所有权值，所以这个策略是有问题的

正确贪心策略：先用二进制枚举行的选择情况，得到所有行的选取方案，然后失去了行的变动干扰，我们再对列求总和并取总和较大的前k-cnt列加入sum中即可，然后多组数据利用max维护一个最终答案answer

解题：  

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 30;
int n,m,k;
int a[N][N];
int col[N];//计算每列总和
int answer;
int calcnt(int num)//计算有多少个1
{
int count = 0;
while(num)
{
count++;
num &= num-1;
}
return count;
}
bool cmp(int a, int b)
{
return a > b;
}
int main()
{
//数据录入
cin >> n >> m >> k;
for(int i = 0; i < n; i++)
for(int j = 0; j < m; j++)
cin >> a[i][j];
//二进制枚举所有行选择情况
for(int i = 0; i < (1 << n); i++)
{
int cnt = calcnt(i);
//非法回合数直接跳过
if(cnt > k) continue;
//多组数据除去残留痕迹
int sum = 0;
memset(col,0,sizeof col);
//完成对行和的累加和列和的统计
for(int x = 0; x < n; x++)
{
for(int y = 0; y < m; y++)
{
if((i >> x) & 1)//当前行被选择
{
sum += a[x][y];
}
else
{
col[y] += a[x][y];
}
}
}
sort(col,col+m,cmp);
for(int j = 0; j <min((k-cnt),m); j++)
{
sum += col[j];
}
answer = max(answer,sum);
}
cout << answer << endl;
return 0;
}

1.calcnt的作用是找到二进制枚举方案中对行进行了几次选取，也就是求出i的二进制表示中有多少个1

2.cmp是传递给sort的仿函数，用于将排序变为降序

3.由于k-cnt有可能大于m，此时去访问col数组可能会出现越界访问，为了避免col的越界访问，我们可以将k-cnt大于m的情况直接变成m

矩阵消除游戏