（学习笔记）2.1 信息存储（2.1.6 布尔代数简介）

文章目录

• 线索栏
• 笔记栏
• • 1.布尔代数基础
  • • 1）起源与定义
    • 2）四种基本运算（见图2-7）
    • 3）与数字逻辑的联系
  • 2. 扩展到位向量
  • • 1）位向量
    • 2）运算规则
    • 3）示例
  • 3. 位向量的应用：表示有限集合
  • • 1)编码方法
    • 2)示例
    • 3)布尔运算 ↔ 集合运算
    • 4)实际应用
  • 4. 练习题解答
  • • 1）练习题2.8
    • 2）练习题2.9（颜色混合）
  • 【网络旁注补充：布尔代数与布尔环】
• 总结栏

线索栏

笔记栏

1.布尔代数基础

1）起源与定义

（1）源于19世纪乔治·布尔的工作，将逻辑值 TRUE(1)​ 和 FALSE(0)​ 代数化。 （2）最基本的布尔代数定义在二元集合 {0, 1}​ 上。

2）四种基本运算（见图2-7）

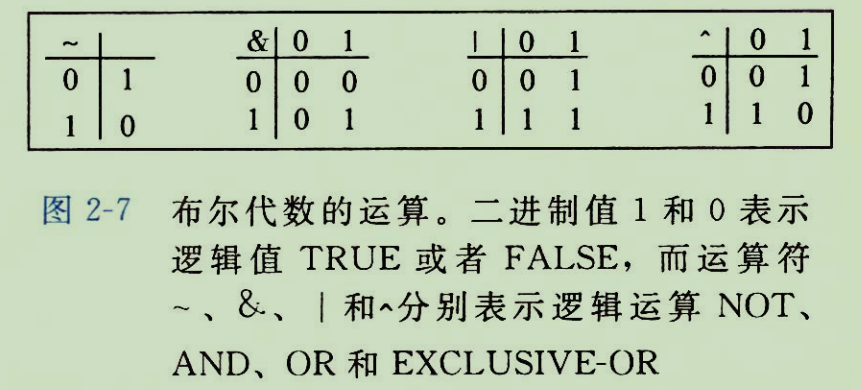（1）NOT（非， ~ 或 ¬）: ~0 = 1, ~1 = 0。 （2）AND（与， & 或 ∧）: 仅当两个操作数均为1时，结果为1。 （3）OR（或， | 或 ∨）: 至少一个操作数为1时，结果为1。 （4）EXCLUSIVE-OR（异或， ^ 或 ⊕）: 两个操作数不同时，结果为1。

3）与数字逻辑的联系

克劳德·香农在其硕士论文中首次建立了布尔代数与数字逻辑（继电器网络）的联系，为现代数字电路设计奠定了数学基础。

2. 扩展到位向量

1）位向量

固定长度为 w的0/1序列。

2）运算规则

对两个位向量进行布尔运算，定义为对它们的每个对应位分别进行相应的布尔运算。

3）示例

设 a = [0110], b = [1100] （1）a & b = [0100] （2）a | b = [1110] （3）a ^ b = [1010]

3. 位向量的应用：表示有限集合

1)编码方法

用长度为 w的位向量可以编码集合 {0, 1, …, w-1}的任何子集 A。规则：当且仅当 i ∈ A时，位向量从右向左数的第 i位为1（a_0是最低位）。

2)示例

（1）位向量 a = [01101001]表示集合 A = {0, 3, 5, 6}。 （2）位向量 b = [01010101]表示集合 B = {0, 2, 4, 6}。

3)布尔运算 ↔ 集合运算

（1）按位或 |​ 对应 集合并集 ∪。 a | b = [01111101]表示 A ∪ B = {0, 2, 3, 4, 5, 6}。 （2）按位与 &​ 对应 集合交集 ∩。 a & b = [01000001]表示 A ∩ B = {0, 6}。 （3）按位取反 ~​ 对应 集合补集。

4)实际应用

例如，操作系统中的信号掩码。用一个位向量来表示一组信号中哪些是有效的（使能），哪些是被屏蔽的。

4. 练习题解答

1）练习题2.8

给定 a = [01101001], b = [01010101] （1）~a = [10010110] （2）~b = [10101010] （3）a & b = [01000001] （4）a | b = [01111101] （5）a ^ b = [00111100]

2）练习题2.9（颜色混合）

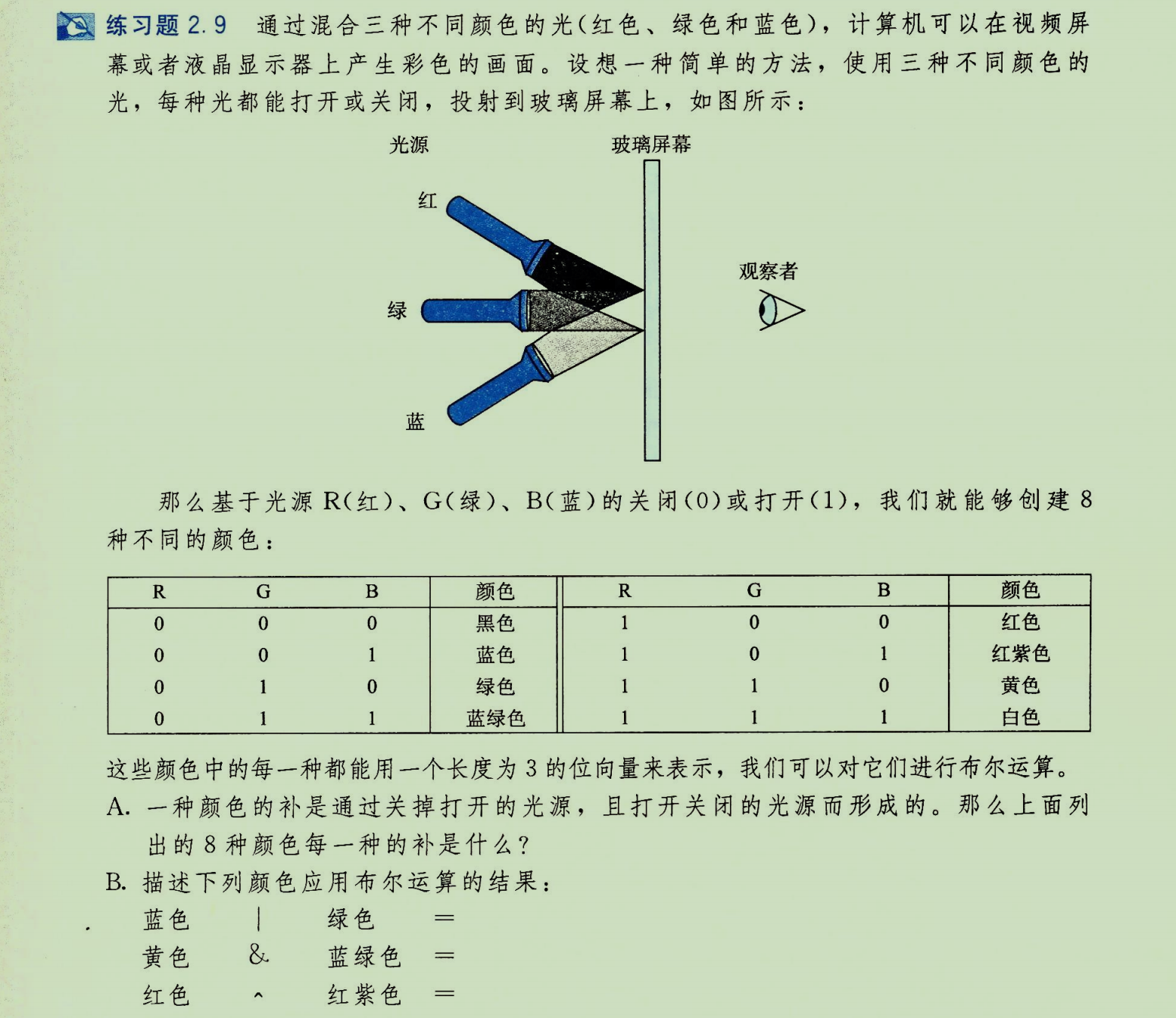颜色编码：用3位向量 [R, G, B]表示颜色（1=开，0=关）。

A. 求补（~）：即颜色取反，关变开，开变关。 （1）黑色(000) ↔ 白色(111) （2）蓝色(001) ↔ 黄色(110) （3）绿色(010) ↔ 红紫色(101) （4）蓝绿色(011) ↔ 红色(100)

B. 布尔运算： （1）蓝色(001) | 绿色(010) = 011，即 蓝绿色​ (Cyan)。 （2）黄色(110) & 蓝绿色(011) = 010，即 绿色​ (Green)。（按位与，只有G位同为1） （3）红色(100) ^ 红紫色(101) = 001，即 蓝色​ (Blue)。（按位异或，不同则为1）

【网络旁注补充：布尔代数与布尔环】

（1）布尔代数：位向量上的 |、&、~运算满足分配律等性质，形成一个代数系统。 （2）布尔环：位向量上的 ^（异或，作为“加法”）和 &（与，作为“乘法”）形成另一个系统，称为布尔环。其特性是每个元素都是自身的加法逆元（a ^ a = 0），由此可推导出如 (a ^ b) ^ a = b等有用性质。

总结栏

本节将抽象的布尔代数与计算机中的位级操作紧密结合：

理解布尔代数和位向量是后续学习位级运算、掩码操作、状态编码以及理解底层硬件逻辑的基础。练习题2.8和2.9是检验理解程度、将理论应用于具体场景的关键实践。