import torch
import matplotlib.pyplot as plt # 导入绘图库,用于可视化
import random # 导入随机模块,用于打乱数据
# ——————– 数据生成 ——————–
def create_data(w, b, data_num):
"""
生成线性回归的合成数据。
参数:
w (Tensor): 真实的权重向量,形状为 (特征数,)
b (Tensor): 真实的偏置标量
data_num (int): 样本数量
返回:
x (Tensor): 特征矩阵,形状 (data_num, 特征数)
y (Tensor): 标签向量,形状 (data_num,)
"""
# 生成特征:从标准正态分布 N(0,1) 中采样,形状 (data_num, len(w))
x = torch.normal(0, 1, (data_num, len(w)))
# 计算线性部分:y = X * w + b,matmul 实现矩阵乘法
y = torch.matmul(x, w) + b
# 添加噪声:从 N(0,0.01) 采样,形状与 y 相同
noise = torch.normal(0, 0.01, y.shape)
y += noise
return x, y
# 设置样本数量
num = 500
# 定义真实的模型参数:权重和偏置
true_w = torch.tensor([8.1, 2, 2, 4]) # 4个特征的权重
true_b = torch.tensor(1.1) # 偏置
# 生成合成数据集
X, Y = create_data(true_w, true_b, num)
# 可视化:只取第4个特征(索引3)与标签的散点图
plt.scatter(X[:, 3], Y, 1) # 点大小为1
plt.show()
# ——————– 数据迭代器 ——————–
def data_provider(data, label, batchsize):
"""
批量数据生成器(每次返回一个批次的数据)。
参数:
data (Tensor): 特征矩阵
label (Tensor): 标签向量
batchsize (int): 批次大小
生成:
(get_data, get_label): 一个批次的特征和标签
"""
length = len(label)
# 生成所有样本的索引列表
indices = list(range(length))
# 随机打乱索引,保证每个 epoch 的数据顺序不同
random.shuffle(indices)
# 按 batchsize 遍历索引
for each in range(0, length, batchsize):
get_indices = indices[each: each + batchsize] # 当前批次的索引
get_data = data[get_indices] # 根据索引取特征
get_label = label[get_indices] # 根据索引取标签
yield get_data, get_label # 生成器返回当前批次
# 设置批次大小
batchsize = 16
# (注释掉的测试代码,可用于验证生成器)
# for batch_x, batch_y in data_provider(X, Y, batchsize):
# print(batch_x, batch_y)
# break
# ——————– 模型定义 ——————–
def fun(x, w, b):
"""
线性回归模型的前向计算。
参数:
x (Tensor): 输入特征矩阵
w (Tensor): 权重
b (Tensor): 偏置
返回:
pred_y (Tensor): 预测值
"""
pred_y = torch.matmul(x, w) + b
return pred_y
def maeLoss(pre_y, y):
"""
平均绝对误差损失函数。
参数:
pre_y (Tensor): 预测值
y (Tensor): 真实值
返回:
标量损失值
"""
return torch.sum(abs(pre_y – y)) / len(y)
def sgd(paras, lr):
"""
随机梯度下降更新参数。
参数:
paras (list): 需要更新的参数列表(包含 w 和 b)
lr (float): 学习率
"""
with torch.no_grad(): # 在此上下文中,不追踪梯度,节省内存
for para in paras:
# 参数更新:参数 = 参数 – 梯度 * 学习率
# 注意:不能写成 para = para – para.grad*lr,因为这会创建新变量,
# 而原地减法 para -= para.grad*lr 会直接修改 para 指向的张量。
para -= para.grad * lr
# 梯度清零:避免梯度累积,影响下一次计算
para.grad.zero_()
# ——————– 参数初始化 ——————–
lr = 0.03 # 学习率
# 初始化权重:从 N(0,0.01) 采样,形状与真实权重相同,并设置 requires_grad=True 以便计算梯度
w_0 = torch.normal(0, 0.01, true_w.shape, requires_grad=True)
# 初始化偏置:标量 0.01,设置 requires_grad=True
b_0 = torch.tensor(0.01, requires_grad=True)
print("初始权重:", w_0, "初始偏置:", b_0)
# ——————– 训练循环 ——————–
epochs = 50 # 训练轮数
for epoch in range(epochs):
data_loss = 0 # 累计当前 epoch 的总损失
# 遍历每个批次的数据
for batch_x, batch_y in data_provider(X, Y, batchsize):
# 1. 前向传播:计算当前批次的预测值
pred_y = fun(batch_x, w_0, b_0)
# 2. 计算损失
loss = maeLoss(pred_y, batch_y)
# 3. 反向传播:自动计算损失关于 w_0 和 b_0 的梯度
loss.backward()
# 4. 使用 SGD 更新参数,并清零梯度
sgd([w_0, b_0], lr)
# 5. 累加损失(注意:loss 是标量张量,累加后仍然是张量)
data_loss += loss
# 打印每个 epoch 的损失
print("epoch %03d: loss: %.6f" % (epoch, data_loss))
# 打印真实参数与学习到的参数对比
print("真实的函数值是", true_w, true_b)
print("训练得到的参数值是", w_0, b_0)
# ——————– 结果可视化 ——————–
idx = 3 # 选择第4个特征进行可视化
# 绘制拟合直线:使用 detach() 从计算图中分离,转换为 numpy 数组进行绘图
# 直线方程:y = x * w_0[idx] + b_0
plt.plot(X[:, idx].detach().numpy(),
X[:, idx].detach().numpy() * w_0[idx].detach().numpy() + b_0.detach().numpy())
# 绘制原始数据散点图
plt.scatter(X[:, idx], Y, 1)
plt.show()
1. 数据准备
-
真实参数:设定真实权重 true_w = [8.1, 2, 2, 4],真实偏置 true_b = 1.1。
-
生成合成数据:调用 create_data(),根据真实参数生成 500 个样本:
-
特征 X 从标准正态分布 N(0,1) 采样。
-
标签 Y 由线性公式 X·w + b 计算,并添加微小高斯噪声 N(0,0.01)。
-
-
可视化:绘制第 4 个特征与标签的散点图,观察数据分布。
2. 模型与超参数定义
-
模型:线性回归 fun(x, w, b) = x·w + b。
-
损失函数:平均绝对误差(MAE) maeLoss()。
-
优化器:手动实现随机梯度下降 sgd(),通过 with torch.no_grad() 原地更新参数并清零梯度。
-
超参数:
-
学习率 lr = 0.03
-
批次大小 batchsize = 16
-
训练轮数 epochs = 50
-
3. 参数初始化
-
权重 w_0 从 N(0,0.01) 采样,偏置 b_0 初始化为 0.01,均设置 requires_grad=True 以计算梯度。
4. 训练循环
每个 epoch 执行以下操作:
数据迭代:通过自定义生成器 data_provider() 打乱数据索引,每次返回一个批次 (batch_x, batch_y)。
前向传播:计算当前批次的预测值 pred_y = fun(batch_x, w_0, b_0)。
损失计算:计算预测值与真实值的 MAE 损失。
反向传播:调用 loss.backward(),自动计算损失对 w_0 和 b_0 的梯度。
参数更新:调用 sgd([w_0, b_0], lr),执行 para -= para.grad * lr 并清零梯度。
损失累计:将当前批次损失累加至 data_loss。
每个 epoch 结束后打印当前损失值。
5. 结果输出与可视化
-
打印训练得到的参数 w_0 和 b_0,与真实参数对比。
-
再次绘制第 4 个特征的散点图,并叠加拟合的直线 x * w_0[3] + b_0,直观展示模型拟合效果。
-
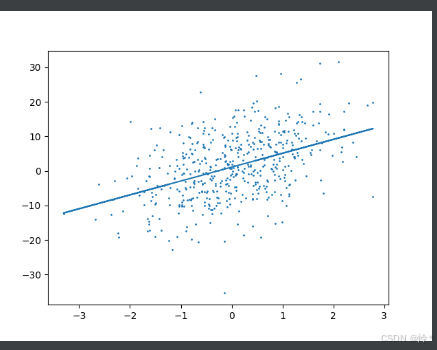
-

 网硕互联帮助中心
网硕互联帮助中心



评论前必须登录!
注册