贝叶斯定理 | 历史溯源、理论推导与统计应用

注：本文为 “贝叶斯定理” 相关合辑。 图片清晰度受引文原图所限。 略作重排，如有内容异常，请看原文。

贝叶斯与贝氏定理 (1)

Thomas Bayes and Bayes’ Theorem (1)

Posted on 2014/11/01

台北市立第一女子高级中学 苏俊鸿 老师

贝氏定理（Bayes’ Theorem）出现在高中数学的概率单元中，被归为条件概率的相关议题，其定理表述如下：

设

{

A

1

,

A

2

,

⋯
 

,

A

n

}

\\{A_1,A_2,\\cdots,A_n\\}

{A1​,A2​,⋯,An​} 为样本空间

S

S

S 的一组分割，

B

B

B 为

S

S

S 的任一事件，若

P

(

B

)

>

0

P(B)>0

P(B)>0，则在事件

B

B

B 发生的条件下，事件

A

k

A_k

Ak​ 发生的概率为

P

(

A

k

∣

B

)

=

P

(

A

k

)

P

(

B

∣

A

k

)

∑

i

=

1

n

P

(

A

i

)

P

(

B

∣

A

i

)

,

1

≤

k

≤

n

\\displaystyle P\\left( A_k \\mid B \\right) = \\frac{P\\left( A_k \\right)P\\left( B \\mid A_k \\right)}{\\sum\\limits_{i = 1}^n P\\left( A_i \\right)P\\left( B \\mid A_i \\right)},\\ 1\\le k\\le n

P(Ak​∣B)=i=1∑n​P(Ai​)P(B∣Ai​)P(Ak​)P(B∣Ak​)​, 1≤k≤n

教材中亦列举了该定理的相关应用，如质量检验、医学检测等。但关于贝叶斯的生平背景、推动该定理诞生的研究问题，以及该定理提出初期是否获得数学家与统计学家的认可，均为多数人所未知。上述问题构成本文的撰写缘起。本文首先阐述托马斯·贝叶斯（Thomas Bayes, 1702-1761）的生平背景，贝氏定理即由其首次提出。

托马斯·贝叶斯出身于英国新教家庭，为家中七名子女中的长子。其父约书亚·贝叶斯（Joshua Bayes）为英国首批受任的六位新教牧师之一。关于贝叶斯的幼年教育，目前可考史料较少。部分历史学者推测其曾受棣美弗（Abraham de Moivre, 1667-1754）的学术指导，亦有学者认为其接受过牧师职业的培养训练。

1719 年，贝叶斯考入苏格兰爱丁堡大学，主修逻辑学与神学。在该历史时期，新教教徒无法获得牛津大学与剑桥大学的入学资格。尽管目前未发现其在爱丁堡大学修习数学的相关记录，但贝叶斯曾于1736 年撰写论文〈流数学说的介绍，以及对《分析学家》作者的反对提出数学家的防御〉（An Introduction to the Doctrine of Fluxions, and a Defence of the Mathematicians Against the Objections of the Author of The Analyst），以反驳贝克莱主教（George Berkeley, 1685-1753）在《分析学家》（The Analyst, 1734）中对微积分逻辑基础的质疑。该论文开篇即指出：

我早就认为流数法的基本原理和规则，需要更为全面且清楚的解释和证明。

该表述直接体现出贝叶斯对流数法的熟练掌握，同时其对贝克莱基于宗教视角提出的相关批评持反对态度。贝叶斯后续被任命为牧师，担任其父的助理神职人员。1733 年之前，其出任Tunbridge Wells（距伦敦35 英里）当地教堂的牧师，直至1752 年卸任该职务，且卸任后仍定居于Tunbridge Wells。

托马斯·贝叶斯

尽管彼时贝叶斯尚未公开发表任何数学相关著作，但其于1742 年当选英国皇家学会院士。该现象与当时的学术风气相关：学者极少以本名在生前发表研究成果，前述1736 年的数学相关论文即为匿名出版。贝叶斯逝世后，其关于

log

⁡

z

!

\\log z!

logz!（该表达式由斯特林与棣美弗提出）的渐近级数敛散性的数学研究成果方得以出版。

贝叶斯在概率论领域的研究成果具有独特的学术价值，其代表性论文为〈《概率论》中一个问题的解决〉（An Essay towards Solving a Problem in the Doctrine of Chances）；其中《概率论》（The Doctrine of Chances, 1718）为棣美弗撰写的概率论领域经典著作。该论文同样于贝叶斯逝世后被其友人理查德·普莱斯（Richard Price, 1723-1791）发现，经普莱斯整理与注释后，于1764 年被送交英国皇家学会，发表于《自然科学会报》（The Philosophical Transactions of the Royal Society）。

该论文中包含了现今广为熟知的条件概率相关论述，以及被命名为贝氏定理的命题。关于贝叶斯开展该项研究的问题缘起与具体论证过程，将在〈贝叶斯与贝氏定理 (2)〉中展开详细阐述。

贝叶斯与贝氏定理 (2)

Thomas Bayes and Bayes’ Theorem (2)

Posted on 2014/11/01

台北市立第一女子高级中学 苏俊鸿 老师

在阐述贝叶斯的论文〈《概率论》中一个问题的解决〉（An Essay towards Solving a Problem in the Doctrine of Chances）的具体内容前，先梳理该历史阶段概率论的发展脉络。法国贵族梅雷骑士（Chevalier de Méré）就骰子掷点、赌金分配等问题向帕斯卡尔（Blaise Pascal, 1623-1662）请教，该问题引发帕斯卡尔与费马（Pierre de Fermat, 1601-1665）通过书信展开讨论并给出解答，该研究工作奠定了概率论的理论基础。

1655 年，荷兰数学家惠更斯（Christiaan Huygens, 1629-1695）到访巴黎，了解到帕斯卡尔与费马的相关讨论问题后产生研究兴趣，并对该类问题展开延伸研究，于1657 年出版专著《论概率博弈的计算》（On the Calculations in Games of Chance）。直至18 世纪初，该书始终为概率论领域的入门著作。

雅各布·伯努利（Jakob I. Bernoulli, 1654-1705）在惠更斯的研究基础上，结合当时保险风险评估等实际应用需求，探究概率论与各类实际问题的结合路径。其逝世8 年后，遗作《猜度术》（Ars Conjectandi, 1713）正式出版，成为概率论领域的经典著作。现今概率论中的大数定律、二项分布等概念，均首次系统呈现于该著作中。伯努利提出，对于任意给定的误差范围，当试验次数足够大时，事件发生的实际次数与试验总次数的比值，与该事件发生的理论概率

p

p

p 之间的偏差将落入该误差范围内。基于该结论可对所需的观测次数进行估算，但伯努利所推导的二项分布近似公式精度不足，无法应用于实际场景的计算。

该研究工作后续由棣美弗完成，其于1733 年推导出现今所称的正态曲线，将其作为二项分布的近似模型，优化了伯努利提出的观测次数估算方法（该曲线后被高斯与拉普拉斯独立重新发现）。棣美武将该方法纳入《概率论》1738 年与1756 年的再版内容中（该书初版于1718 年）。从贝叶斯的论文标题〈《概率论》中一个问题的解决〉可看出，其研究工作以棣美弗的研究成果为理论基础。该论文开篇即明确其研究问题：已知某未知事件（发生概率未知）的发生次数与未发生次数，求解该事件在单次试验中发生的概率值介于两个指定概率值之间的概率。

以现代数学符号表述该问题：设

X

X

X 为

n

n

n 次试验中该事件的发生次数，

x

x

x 为该事件在单次试验中发生的概率值，

r

,

s

r,s

r,s 为两个指定概率值且满足

r

<

s

r<s

r<s，则贝叶斯的研究问题可表示为：

P

(

r

<

x

<

s

∣

X

)

=

?

P(r<x<s \\mid X)=?

P(r<x<s∣X)=?

贝叶斯采用公理化的论证体系，先给出相关定义，再提出相应命题，其中下述两个代表性命题如下：

• 命题 3 两个相继发生事件的联合概率为一比值，由第一个事件发生的概率，与第一个事件发生的条件下第二个事件发生的条件概率复合得到。
• 命题 5 若存在两个相继发生的事件，已知第二个事件发生的概率为 $\frac{b}{N}$

设事件

E

E

E 为第一个事件，事件

F

F

F 为第二个事件，则命题3 对应现今的条件概率乘法公式：

P

(

E

∩

F

)

=

P

(

E

)

P

(

F

∣

E

)

P(E\\cap F)=P(E)P(F \\mid E)

P(E∩F)=P(E)P(F∣E) 命题5 即为贝氏定理，用于求解事件

F

F

F 发生条件下事件

E

E

E 发生的条件概率：

P

(

E

∣

F

)

=

P

(

E

∩

F

)

P

(

F

)

P(E \\mid F) = \\frac{P(E \\cap F)}{P(F)}

P(E∣F)=P(F)P(E∩F)​

若将事件

F

F

F 定义为「

n

n

n 次试验中该事件的发生次数为

X

X

X 次」，将事件

E

E

E 定义为「该事件单次试验的发生概率满足

r

1

<

x

<

r

2

r_1<x<r_2

r1​<x<r2​」，则贝叶斯的研究问题即为求解条件概率

P

(

E

∣

F

)

P(E \\mid F)

P(E∣F)。欲求解该概率，需先计算

P

(

F

)

P(F)

P(F) 与

P

(

E

∩

F

)

P(E\\cap F)

P(E∩F) 的值。贝叶斯通过极具独创性的思路构建概率模型，完成上述两个概率值的计算，其具体方法将在〈贝叶斯与贝氏定理 (3)〉中展开阐述。

贝叶斯与贝氏定理 (3)

Thomas Bayes and Bayes’ Theorem (3)

Posted on 2014/11/01

台北市立第一女子高级中学 苏俊鸿 老师

本节阐述贝叶斯求解

P

(

F

)

P(F)

P(F) 与

P

(

E

∩

F

)

P(E\\cap F)

P(E∩F) 的具体方法，其通过极具独创性的思路构建概率模型，完成该计算过程。如图1 所示，考虑水平放置的正方形桌面（平面

A

B

C

D

ABCD

ABCD），将球

O

O

O 与球

W

W

W 抛掷至该桌面，且假设两球落在桌面任意面积相等区域内的概率相等。

首先抛掷球

W

W

W，过球

W

W

W 的落点作直线

o

t

ot

ot 平行于边

A

D

AD

AD，该直线分别与边

C

D

CD

CD、边

A

B

AB

AB 相交于点

t

t

t 与点

o

o

o。随后将球

O

O

O 抛掷

p

+

q

=

n

p+q=n

p+q=n 次，若单次抛掷中球

O

O

O 落于边

A

D

AD

AD 与直线

o

t

ot

ot 之间的区域，则称该次试验中事件

M

M

M 发生。

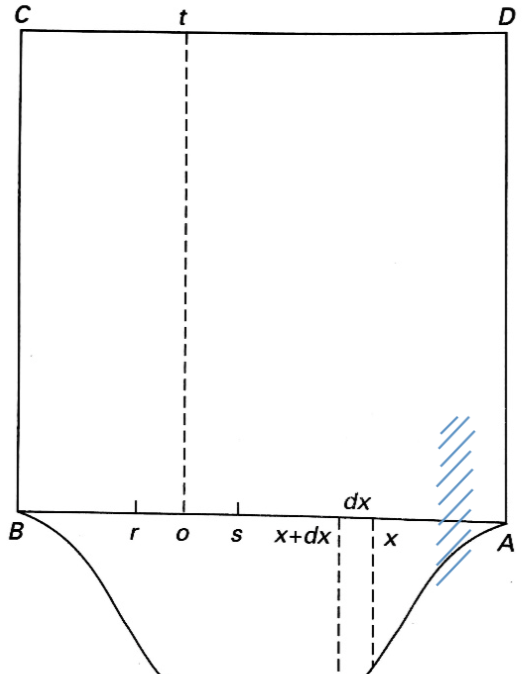
图1

为便于后续推导说明，不妨设正方形的边长

A

B

‾

=

1

\\overline{AB}=1

AB=1。根据贝叶斯的模型设定，球

W

W

W 的落点位置决定了事件

M

M

M 发生的概率

x

x

x，且点

o

o

o 落于点

r

r

r 与点

s

s

s 之间的概率，可由线段

r

s

‾

\\overline{rs}

rs 的长度表示。因此，在球

W

W

W 抛掷完成后，事件

M

M

M 发生的条件概率等于线段

A

o

‾

\\overline{Ao}

Ao 的长度。

反之，对于任意给定的概率范围，均可表示为边

A

B

‾

\\overline{AB}

AB 上的一个区间，记为

[

x

,

x

+

d

x

]

[x,x + dx]

[x,x+dx]。若将

x

x

x 定义为球

O

O

O 落于直线

o

t

ot

ot 右侧区域的概率，则

1

−

x

1-x

1−x 为球

O

O

O 落于直线

o

t

ot

ot 左侧区域的概率。因此，在

p

+

q

=

n

p+q=n

p+q=n 次抛掷试验中，球

O

O

O 有

p

p

p 次落于直线

o

t

ot

ot 右侧区域的概率为：

y

=

C

n

p

x

p

(

1

−

x

)

q

=

C

n

p

x

p

(

1

−

x

)

n

−

p

y = \\mathrm{C}_n^p x^p (1 – x)^q = \\mathrm{C}_n^p x^p (1 – x)^{n-p}

y=Cnp​xp(1−x)q=Cnp​xp(1−x)n−p

贝叶斯随后在边

A

B

‾

\\overline{AB}

AB 的下方绘制出函数

y

=

C

n

p

x

p

(

1

−

x

)

n

−

p

y = \\mathrm{C}_n^p x^p (1 – x)^{n-p}

y=Cnp​xp(1−x)n−p 对应的曲线（该函数形式借鉴棣美弗的研究成果）。由命题3 可得乘法公式

P

(

E

∩

F

)

=

P

(

E

)

P

(

F

∣

E

)

P(E \\cap F) = P(E)P(F \\mid E)

P(E∩F)=P(E)P(F∣E)，因此球

W

W

W 的落点位于区间

[

x

,

x

+

d

x

]

[x,x + dx]

[x,x+dx] 上方，且球

O

O

O 有

p

p

p 次落于球

W

W

W 右侧区域的联合概率，可由区间

[

x

,

x

+

d

x

]

[x,x + dx]

[x,x+dx] 下方与上述曲线所围成的区域（斜线标注区域）的面积表示。

因此，联合概率

P

(

E

∩

F

)

=

P

(

(

r

<

x

<

s

)

∩

(

X

=

p

)

)

P(E \\cap F) = P((r < x < s) \\cap (X = p))

P(E∩F)=P((r<x<s)∩(X=p)) 等于区间

[

r

,

s

]

[r,s]

[r,s] 下方与该曲线所围成的区域面积，以现代积分符号表示为：

∫

r

s

C

n

p

x

p

(

1

−

x

)

n

−

p

d

x

\\int_r^s \\mathrm{C}_n^p x^p (1 – x)^{n-p} dx

∫rs​Cnp​xp(1−x)n−pdx

同理，联合概率

P

(

F

)

=

P

(

(

0

<

x

<

1

)

∩

(

X

=

p

)

)

P(F) = P((0 < x < 1) \\cap (X = p))

P(F)=P((0<x<1)∩(X=p)) 等于边

A

B

‾

\\overline{AB}

AB 与该曲线所围成的区域面积，其积分表达式为：

∫

0

1

C

n

p

x

p

(

1

−

x

)

n

−

p

d

x

\\int_0^1 \\mathrm{C}_n^p x^p (1 – x)^{n-p} dx

∫01​Cnp​xp(1−x)n−pdx

因此，由命题5 可推得：

P

(

E

∣

F

)

=

P

(

E

∩

F

)

P

(

F

)

=

∫

r

s

C

n

p

x

p

(

1

−

x

)

n

−

p

d

x

∫

0

1

C

n

p

x

p

(

1

−

x

)

n

−

p

d

x

\\displaystyle P(E \\mid F) = \\frac{P(E \\cap F)}{P(F)} = \\frac{\\int_r^s \\mathrm{C}_n^p x^p (1 – x)^{n-p} dx}{\\int_0^1 \\mathrm{C}_n^p x^p (1 – x)^{n-p} dx}

P(E∣F)=P(F)P(E∩F)​=∫01​Cnp​xp(1−x)n−pdx∫rs​Cnp​xp(1−x)n−pdx​

由上述推导结果可得出结论：事件

M

M

M 发生的概率，可仅通过该事件在一定次数试验中的发生次数与未发生次数确定，无需其他额外信息，只需通过计算上述积分对应的区域面积即可求解该概率值。

贝叶斯从形式上解决了该研究问题，其研究成果进入统计推断的研究范畴，但该方法的实际应用仍存在两个亟待解决的问题：其一，该公式分子与分母中的积分计算（即区域面积求解）具有较高的运算难度；其二，该推导过程基于思想实验的建模方式，通过抛球试验构建的概率模型是否能准确对应实际场景中的概率问题，尚存争议。此外，贝叶斯在建模中仅考虑

X

=

0

,

1

,

2

,

⋯
 

,

n

X=0,1,2,\\cdots,n

X=0,1,2,⋯,n 取各值时概率相等的情形，其建模依据为「无理由认为该事件在一定次数的试验中，发生次数会偏向某一取值而非其他取值」。

该假设引发了诸多学术争论，争论的焦点问题为：在未知某事件发生概率的前提下，是否可直接认定该事件发生次数的所有可能结果均具有相等的概率？此外，贝氏定理所体现的思想为「通过新获取的信息，将事件的先验概率更新为后验概率」，该思想与20 世纪初期兴起的频率论（frequentism）统计学的相关思想存在冲突。因此，贝氏定理在该历史阶段长期未得到学界的广泛关注，实属必然。

但进入21 世纪后，基于贝氏定理发展而来的各类应用已广泛应用于各类场景，如Google 搜索的词条筛选、无人驾驶车辆的行驶位置判定等。该发展历程的详细脉络可参考Sharon McGrayne 所著《不死的定理》（The Theory That Would Not Die: How Bayes’ Rule Cracked the Enigma Code, Hunted Down Russian Submarines, and Emerged Triumphant from Two Centuries of Controversy, Yale University Press, 2011）。

参考文献

• Katz, V. J. (1993), A History of Mathematics, New York: HarperCollins College Publishers.
• Biography of Thomas Bayes, http://www-history.mcs.st-and.ac.uk/Biographies/Bayes.html
• An Essay towards Solving a Problem in the Doctrine of Chances. By the Late Rev. Mr. Bayes, F. R. S. Communicated by Mr. Price, in a Letter to John Canton, A. M. F. R. S. https://archive.org/stream/philtrans09948070/09948070#page/n0/mode/2up
• 陈昱成,〈贝氏定理的应用〉,《科学教育月刊》第357 期(2013),页19-28｡

via:

• 貝葉斯和貝氏定理(1)（Thomas Bayes and Bayes’ Theorem (1)） | 2014 https://case.ntu.edu.tw/highscope/貝葉斯和貝氏定理1（thomas-bayes-and-bayes-theorem-1）/index.html
• 貝葉斯和貝氏定理(2)（Thomas Bayes and Bayes’ Theorem (2)） | 2014 https://case.ntu.edu.tw/highscope/貝葉斯和貝氏定理2（thomas-bayes-and-bayes-theorem-2）/index.html
• 貝葉斯和貝氏定理(3)（Thomas Bayes and Bayes’ Theorem (3)） | 2014 https://case.ntu.edu.tw/highscope/貝葉斯和貝氏定理3（thomas-bayes-and-bayes-theorem-3）/index.html