C语言数据结构--二叉树和堆

一、树

1.1什么是树？

树是一种非线性的数据结构，它有n个有限结点组成的一个具有层次关系的集合，形状上可以比作一颗倒挂的树，所以我们称作树，树的特点是根在上，叶在下。

• 有一个特殊的结点，称为根结点，根结点没有前驱节点
• 除了根结点之外，其余结点被分成M（M>0)个互不相交的集合T1，T2，……，Tm，其中每一个集合又是一棵结构与树类似的子树。每棵字数的根结点有且只有一个前驱（父节点），可以有大于等于0个后续（子结点）
• 树是递归定义的
  
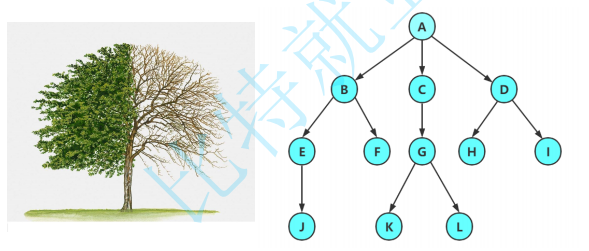
  注意：任意子树之间不可有交集否则就不是树

1.2树的相关概念

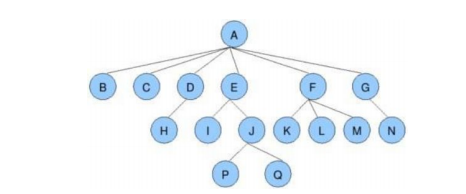
• 结点的度：一个结点含有的子树的个数称为该结点的度； 如上图：A的度为6
• 叶结点或终端结点：度为0的结点称为叶结点； 如上图：B、C、H、I…等结点为叶结点
• 非终端结点或分支结点：度不为0的结点； 如上图：D、E、F、G…等结点为分支结点
• 双亲结点或父结点：若一个结点含有子结点，则这个结点称为其子结点的父结点； 如上图：A是B的父结点
• 孩子结点或子结点：一个结点含有的子树的根结点称为该结点的子结点； 如上图：B是A的孩子结点
• 兄弟结点：具有相同父结点的结点互称为兄弟结点； 如上图：B、C是兄弟结点
• 树的度：一棵树中，最大的结点的度称为树的度； 如上图：树的度为6
• 结点的层次：从根开始定义起，根为第1层，根的子结点为第2层，以此类推
• 树的高度或深度：树中结点的最大层次； 如上图：树的高度为4
• 堂兄弟结点：双亲在同一层的结点互为堂兄弟；如上图：H、I互为兄弟结点
• 结点的祖先：从根到该结点所经分支上的所有结点；如上图：A是所有结点的祖先
• 子孙：以某结点为根的子树中任一结点都称为该结点的子孙。如上图：所有结点都是A的子孙
• 森林：由m（m>0）棵互不相交的树的集合称为森林

1.3树的表示

树的结构相对线性表比较复杂，要存储表示起来比较麻烦，既要保存值也要保存结点和结点之间的关系，实际操作中树有很多种表示方法：如双亲表示法，孩子表示法，孩子双亲表示法以及孩子兄弟表示法等等。这里我们就简单了解其中一种最常用的：左孩子，右兄弟表示法。

typedef int DataType;
struct Node
{
struct Node* firstChild1; // 第一个孩子结点
struct Node* pNextBrother; // 指向其下一个兄弟结点
DataType data; // 结点中的数据域
};

直观展示：

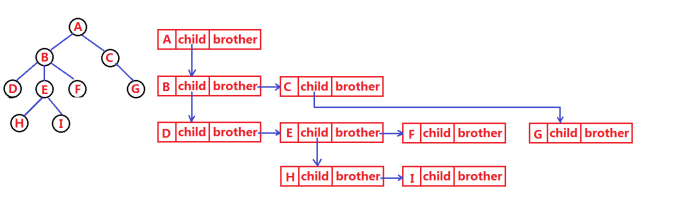
1.4树在实际中的运用

电脑的文件管理器，C盘或D盘可以看作一个根结点，它的下一级文件夹作为它的子结点，这些子文件夹又有下一级子文件夹作为它们的子结点，所以这些子文件夹同时也扮演父节点的角色。

二、二叉树

2.1二叉树的概念

二叉树是树的子集，一棵二叉树是一个包含有限个结点的集合，或者说是结点的一个有限集合，该集合的特点：

由一个根结点加上两棵别称为左子树和右子树的二叉树组成

二叉树的子树由左右之分，次序不可颠倒，因此二叉树是有序树
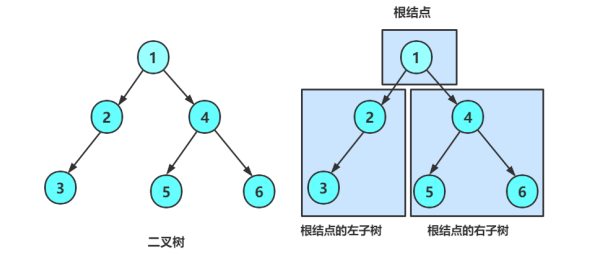
注意：对于任意的二叉树都是由以下几种情况复合组成

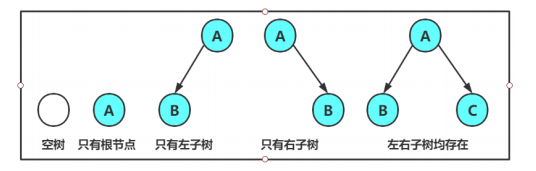
现实中的二叉树：

2.2特殊的二叉树

2.2.1满二叉树

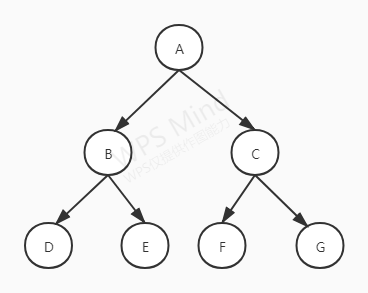
如图，一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。也就是说，如果一个二叉树的层数为K，且结点总数是$$2^k-1$$，则它就是满二叉树。

2.2.2完全二叉树

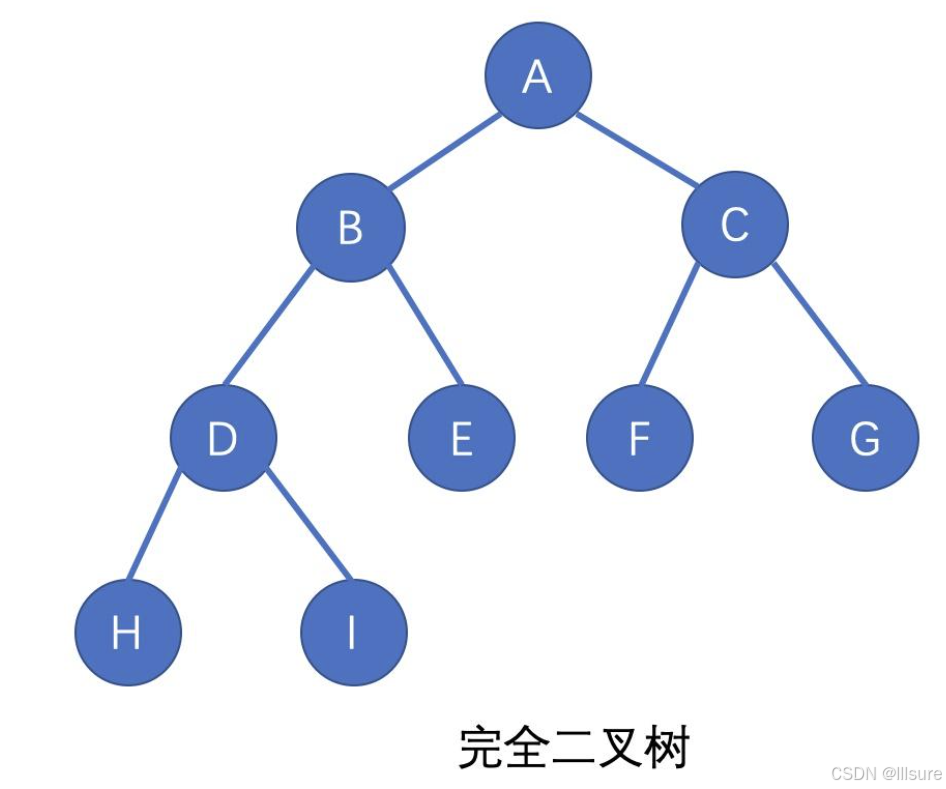
如图，完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
注意满二叉树是一种特殊的完全二叉树

2.3二叉树的性质（重要）

/*
* 假设二叉树有N个结点
* 从总结点数角度考虑：N = n0 + n1 + n2 ①
*
* 从边的角度考虑，N个结点的任意二叉树，总共有N-1条边
* 因为二叉树中每个结点都有双亲，根结点没有双亲，每个节点向上与其双亲之间存在一条边
* 因此N个结点的二叉树总共有N-1条边
*
* 因为度为0的结点没有孩子，故度为0的结点不产生边; 度为1的结点只有一个孩子，故每个度为1的结
点* * 产生一条边; 度为2的结点有2个孩子，故每个度为2的结点产生两条边，所以总边数为：
n1+2*n2
* 故从边的角度考虑：N-1 = n1 + 2*n2 ②
* 结合① 和 ②得：n0 + n1 + n2 = n1 + 2*n2 – 1
* 即：n0 = n2 + 1
*/

更多性质：

• 若规定根结点的层数为1，具有n个结点的满二叉树的深度，h=以2为底（n+1）的对数。
• 对于具有n个结点的完全二叉树，如果按照从上至下从左至右的数组顺序对所有结点从0开始编号，则对于序号为i的结点有：
  • 若i>0，i位置结点的双亲序号：(i-1)/2；i=0，i为根结点编号，无双亲结点
  • 若2i+1<n，左孩子序号：2i+1，2i+1>=n否则无左孩子
  • 若2i+2<n，右孩子序号：2i+2，2i+2>=n否则无右孩子

2.4二叉树的存储

用数组存储二叉树具有天然的优势，用数组的这种存储，我们称之为顺序存储，一般使用数组只适合表示完全二叉树，因为不是完全二叉树会有空间的浪费。而现实中使用中只有堆才会使用数组来存储，关于堆我们后面的章节会专门讲解。二叉树顺序存储在物理上是一个数组，在逻辑上是一颗二叉树。

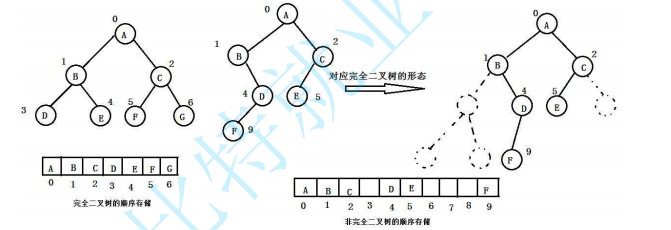
当然二叉树也可以用链式结构进行存储，这里不作介绍。

三、堆

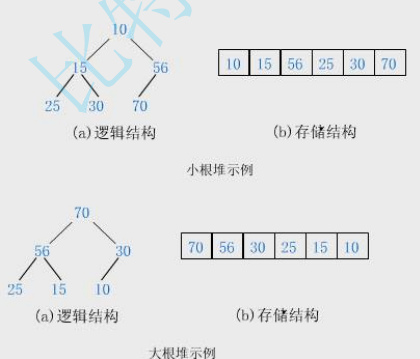
堆是完全二叉树的一种，结构上必须严格遵守完全二叉树的规则，在此基础上再满足值的大小规则（大根堆/小根堆）。

四、结于

本篇主要介绍C语言中的数据结构，树，详细介绍了树的概念何性质，以及存储结构，并借此引出了堆的介绍，堆是完全二叉树，且分为大堆和小堆，大堆的任意父节点的值大于其子结点的值，小堆则相反，这是堆特有的值的规则，光有完全二叉树的结构特性而不满足值的规则，则不构成堆。

若文中存在任何错误，欢迎各位批评指正，大家共同进步