前言
本文基于C语言描述
正确食用方式:有C语言基础,仅熟悉单向链表基本操作且迫切需要实战进行巩固。
满足这些条件的小伙伴们,本文非常值得你一啃!阅读本文,你收获的将远不止是会解这三道题,更能收获”面对陌生算法题,该如何开始思考“等拆解算法问题的通用方法,这也是本文主打内容。
同时欢迎各位大佬前来纠错。
LeetCode 206(反转链表)、21(合并两个有序链表)、23(合并K个有序链表)本文将由浅入深地带你理顺逻辑,即使是新手也能很快上手。
新人第一次发文,本文文本、链表相关图片、动图演示皆属原创,创作不易,求点赞!
喜欢本文风格或是认可本文思想的话,可以点个关注,助力我今后肝出更多优质好文!
目录
前言
本文基于C语言描述
一、基础铺垫
1.节点与表头
2.链表的统一
3.哑元节点(虚拟头节点)
二、详细解析
1.反转链表-简单
1.1题目分析
1.2思路推导
1.2.1头插法
1.2.2递归法
1.2.3双指针迭代法
2.合并两个有序链表-简单
2.1 题目分析
2.2 思路推导
2.2.1 迭代法(主链实现)
2.2.2 迭代法(对称实现)
2.2.3 递归法
3.合并K个升序链表 – 中等
3.1题目分析
3.2 思路推导
3.2.1 ”暴力串珠法“
3.2.2 暴力迭代法
3.2.3 优先队列法(最小堆实现)
3.2.4 分治合并法(迭代实现-自底向上)
3.2.5分治合并法(递归实现-自顶向下)
三、总结
1. 核心题型与解题方法梳理
1.1 反转链表(LeetCode 206)
1.2 合并两个有序链表(LeetCode 21)
1.3 合并K个升序链表(LeetCode 23)
2. 通用解题思维与优化技巧
2.1 边界处理优先
2.2 指针管理是核心
2.3 暴力思路是优化的起点
2.4 复用基础逻辑,拆解复杂问题
3.方法抉择与场景适配
4.学习收获与后续延伸
4.1 核心收获
4.2 后续延伸
四、结语
一、基础铺垫
此部分帮助部分读者进行基础回顾,如果基础扎实,请直接跳转至实战及讲解部分。
1.节点与表头
无论你师从何处,讲到链表的表示时,都会涉及到三种表示方法: “裸指针”(链表的一种表现方式,表现为无结构体封装表头的裸露头指针)、头指针、头节点,这是最基础的概念。
typedef struct link_node{
element_t data;
struct link_node *next;
}LNode;
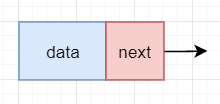
[实现链表的基础节点] data表示数据域,next表示指针域。

由于链表离散储存的性质,我们想要知道一个节点存储着什么样的信息,前提是有指向该节点的指针。如此一来,每个节点都有一个前置节点的next指向它,以保证数据不会在茫茫人海中丢失。然而,这样的指向总需要一个起头,毕竟现实支撑不了希尔伯特酒店的无限规模。你可能会想到头尾相接的循环链表。非常聪明!但循环链表并不是我们本次讨论的重点,这的确是一种方法。顺着思路,我们发现需要一个表头来管理这些容易跑丢的指针。

[裸指针表示的头节点]
如此,就非常自然的形成了“裸指针”的表示方法。(下文不再标注引号,无特别说明时,“裸指针”全都特指这种链表的表示方式而不是指针本身)
2.链表的统一
作为初学者,你会不禁思考,这样自然的表示方法不是足够了吗?我们何必大费周章地去额外封装结构体作为一个表头?这似乎破坏了链表的统一性——这也是在我初学时期困扰过我的一个问题。实则恰恰相反,只有当我们实际操作后就会明白,我们所写的操作函数,大多都是以节点为单元进行操作,而裸指针的存在将会打破这一统一的逻辑。例如头插法的实现:
//内置辅助函数,直接操控节点,用于统一插入逻辑
static int insertLNode(LNode* prev,element_t val){
LNode* node = (LNode*)malloc(sizeof(LNode));
if(!node) return 0;
node->data = val;
node->next = prev->next;
prev->next = node;
return 1;
}

…
LNode* prev = &header;//错误写法
if(insertLNode(prev,val)) {
num++;
}
…
从动画可以很方便地看出,我们在插入节点时,为了维护链表,避免丢失,必须让新节点的next来接替head指针的工作,之后head才能放心移开,否则就会直接造成丢失。动画虽然方便,但指针的移动却没有这么轻松。当我们尝试向上述代码一样描述插入过程时,很快就会发现。head作为裸指针没有实质的节点。这也导致prev->next实际是首元节点的next,第一个节点的元素始终无法改变位置。只会插入在它的后续位置。不仅如此,当空表时如果将head作为prev的实参传入,将会直接导致崩溃。这也是我们封装表头的原因之一。
//带头节点的链表
typedef struct {
LNode header;
int num;
}LinkTable;
//带头指针的链表
typedef struct {
LNode* ptr_head;
int num;
}LinkList;

带头节点的链表的确能解决刚才的问题,但带头指针的链表好像跟刚才裸露指针的情况相比也没差,仅仅是增加了一个用于计节点数的int变量num。的确,头指针和刚才并没有多大区别,但是在使用裸露指针的情况下,我们会面临一个很多新手容易栽的坑——修改形参而未改实参。
解决方法
1.返回值更新
2.传二级指针
3.结构体封装
联想一下你当初学习指针时的场景。我们的选择是要么将函数的修改部分作为返回值返回,要么直接在函数内部解引用指针。在这里也是如此,只不过要在函数内修改指针(类似prev = prev->next;的操作),则需要使用二级指针。这会带来理解门槛高、容易出错、阅读性差等诸多问题。而结构体则更加灵活、安全、易维护。种种特性,以及原因,在这里就不展开说了,直接给出两种情况对应的头插法代码:
//带头节点
void insertHeaderTable(LinkTable *table,element_t val) {
LNode* prev = &table->header;
if(insertLNode(prev,val)) {
table->num++;
}
}
//带头指针
void insertHeaderList(LinkList* list,element_t val) {
LNode header;
header.next = list->ptr_head;
LNode* prev = &header;
if (insertLNode(prev,val)) {
list->ptr_head = header.next;
list->num++;
}
}
为了解决前置节点的问题,我们选择用一个不存放数据的节点作为哨兵节点,来辅助头插法的逻辑统一。对于头指针的情况,我们只需在函数栈空间上自动分配头节点,并随函数栈帧销毁而自动回收,即可实现和带头结点链表操作逻辑的统一,无需区分空表与非空表的边界情况。
3.哑元节点(虚拟头节点)
说完了封装表头的诸多好处,但在leetcode上题目大多不会额外封装结构体,而是采用返回值更新的方式开放作答接口供我们答题。我们仍然可以效仿之前的逻辑。分配哑元节点dummy。
LNode* insertLink(LNode* head,element_t val) {
LNode dummy;
dummy.next = head;
LNode* prev = &dummy;
if (insertLNode(prev,val)) {
return dummy.next;// <————
}
printf("insertLink Failed!\\n");
return head;
}
这里值得注意的是,箭头标记处为何要返回dummy.next?

通过图片可以直观理解,哑元节点只是起临时的辅助作用,会在函数栈帧销毁时随之被回收。如果我们不通过返回值去更新首元节点的地址head则是做了无用功。因为插入新的节点时,头指针应该随之改变。其他的操作逻辑,此处就不过多展开了。概念十分简单,如果你感到理解困难,请务必先上手敲敲键盘,画画图,这将有助于你理解和熟悉。
接下来进入实战部分。
二、详细解析
1.反转链表-简单


作答接口:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
struct ListNode* reverseList(struct ListNode* head) {
//此处填写代码
}

1.1题目分析
先说结论:看到 反转链表,直接反应到考“指针反转”的核心操作,有三种解题方法:
时间复杂度 空间复杂度
1.头插法 O(n) O(1)
2.递归法 O(n) O(n)
3.迭代法 O(n) O(1) “最优解”
模式识别后,立刻调用双指针迭代固化的模板,分别用两个指针记录“前驱”和“当前”,遍历过程中完成反转。
struct ListNode* reverseList(struct ListNode* head) {
struct ListNode *prev = NULL;
struct ListNode *curr = head;
while (curr) {
struct ListNode* next = curr->next;
curr->next = prev;
prev = curr;
curr = next;
}
return prev;
}
需要注意的是,三种方法的抉择并不是考场或面试时临时思考的内容,而是之前学习过程中积累的经验。详解稍后见第三部分。

*需要注意的是动画最后next还进行了移动,实际没有发生,next在实际操作中只是临时变量,和curr绑定在一起只为了方便动画演示。
1.2思路推导

正题
当我们第一次接触这题时,我们不会从一开始就设想通过双指针迭代去进行一个反转指针的操作。(不排除您非常聪明)正常的思维应当是从我们【会什么】开始。我可以设想重新创建一个链表,每次读取题目链表的最后一位,然后依次往前,赋值给新的链表。诚然,这样的方法很“蠢”,却可以作为我们思考的起点。
有了这个思考锚点过后,我们应该着手思考它为什么直觉上就很“蠢”?换言之弊端在哪?
反题
1.题干给出为单向链表,从尾到头读取必然效率极低 O(n²)
2.逻辑冗余,看似符合直觉,实际代码为了围绕思考锚点转会出现大量可直接化简的冗余。
3.额外占用 O(n) 的空间,这种做法甚至可以变为直接读取存入数组,再新建链表,符合直觉但空间开销大
我们逐个去解决这些弊端,看看能不能得到一个最终优化版本,而这个版本至少能为我们开路。
能不能从头到尾?——优化遍历方式
放弃从尾到头读取,改为正向遍历,我们先假设把链表的数据全部读入数组。只进行了一次O(n)的必然需要的读取操作
能否找到不用主动贴合的闭环逻辑?——优化实现逻辑
先不管空间或时间,刚才我们过度关注实现的过程,现在不妨重新聚焦目的——需要一个新链表,那就可以用我们已经固化的头插法逻辑来尝试实现逻辑闭合。
能不能原地变换 ?——优化空间使用
原地变换,为了优化空间,题目给出的链表各个节点本身所占空间就极其宝贵。如同穿珠子一样,珠子本身不动,但我们可以反过来穿,只需调转指针方向即可优化
合题
我们可以尝试进行简单的排列组合看看会发生什么。
1.2.1头插法
综合两点,我们既需要正向遍历,又要用头插法的固化逻辑,且暂时不考虑空间问题。不妨新建一个链表试试看。
当我们准备插入新节点的适合,自然想到,我可以直接利用题给的链表空间而无需主动申请和销毁堆空间。如此一来,弊端3也被顺带解决了。
我们想到直接拿节点来用,但首元节点还含有后面的节点的信息。于是我们可以新建指针ListNode*curr来保护后续节点。此时首元节点彻底自由,下一步它需要解放上一个节点,虽说哑元节点直接指向NULL,但我们也视作保护对象,如此一来就统一了代码逻辑。接着推演,当前置节点的next被解放后,就可以直接指向下一个节点。这个时候我们惊讶的发现,逆转指针的操作被我们用一种类似入栈的方式解决了,由于先入后出,压入底部的节点也就从首元节点翻转为尾节点。

需要注意的是,curr一开始不应该指向NULL,而应该指向头节点,此处纯属演示失误,但无伤大雅。
代码实现如下:
typedef struct ListNode ListNode;
struct ListNode* reverseList(struct ListNode* head) {
ListNode dummy; //哑元or虚拟头节点
dummy.next = NULL;
ListNode* curr = head;//不能为NULL,确保能进循环
while(curr){
curr = head->next;//保护后续指针
head->next = dummy.next;//head->next 即当前节点的next被解放,进而解放哑元节点的工作
dummy.next = head;//同理
head = curr;//新头换旧头
}
return dummy.next;//返回新链表的头,dummy随函数栈帧的销毁随之被回收
}
时间复杂度:O(N) (while循环遍历一遍全部节点)

这样就已经实现了时间复杂度最优的解法,不妨继续进行其他方法的尝试。虽然刚才空间开销的问题被顺带解决了,但反转指针的想法还没有进行尝试。我们可以先来进行思考实验,如果我们什么都不考虑,直接调转指针会发生什么。

很好,从图可以看出,五号节点的指针成功完成了倒转,虽然五节点指向的NULL不是需要被保护的内容,但是这样的操作仍然让我们缺乏安全感。我们继续推演。

这个时候问题就真正地暴露出来了,因为四号节点的职责冲突,它同时承担了保护五号节点和反转操作的责任。这让它不堪重负,直接放弃了五号节点。最直接的结果就是五号节点的信息丢失。
我们先不急着去“马上派遣一个指针管理尾节点”。所谓谋定而后动。先仔细思考和实际操作相比,有哪些需要优化的部分? 分担职责当然算一个,另外一个重要的事情其实被我们忽略了,图片演示的直观性,我们预设了我们拥有可以操控全局的指针指向这个能力。但实际我如果去动尾节点的话,是需要从头到尾先遍历一遍链表的,遍历的结束条件curr->next = NULL,这里直接形成了局部的循环,会导致结束条件始终为假,造成死循环。这是其次,我们可以通过让反转后指向的节点的next = NULL来解决,如果继续推演的话的确是可行的。但最大的问题在于这样得出的方法时间复杂度上界为O(n²)。我们在找尾节点的时候只是在往后找,而什么都没有干,把宝贵的遍历次数浪费了。所以我们应该聚焦的是“做些什么”。
最暴力的办法就是,curr走到每个节点时都用一个指针指着这个节点,直接用数组存起来,问题在于题目没有给我们节点的数量。于是我们可以在堆上维护一个动态数组。这是可行的,虽然看上去有点傻,但是已经非常贴近递归法的实现逻辑了,我们正常去讲递归是怎么去理解的?
1.2.2递归法

假设我们的反转工作已经做到最后一步,正如动画所示,只需要head->next=NULL即可。此时我们要返回的指针是哪个呢?newhead4。我们将这个过程抽离出来

就能清晰地看出,首先让head->next->next(即节点2的next)指向head指向的目标(节点1)。再让head->next = NULL来解除”互指“状态。接着我们返回newhead。这就是整个reverse函数干的事情。非常清晰,非常干脆。我们输入的是左边的指针。返回的却是右边的指针。这具有某种传递性。回到前面五个结点的链表图。我们现在只要reverse干”一件“事情——给左边的指针,返回给我右边的指针。
typedef struct ListNode ListNode;
//只能实现两个节点间指针反转的reverse函数
struct ListNode* reverseList(struct ListNode* head) {
if(head || head->next) return NULL;
ListNode* newhead = head->next;
head->next->next = head;
head->next = NULL;
return newhead;
}
//调用时
{
ListNode* newhead1 = reverseList(head);
ListNode* newhead2 = reverseList(newhead1);
// ……
}
这样来看,我们是不是还差”临门一脚“?
ListNode* newhead1 = reverseList(head);
ListNode* newhead2 = reverseList(newhead1);
//……
//相当于–>ListNode* newhead2 =
//reverseList(reverseList(…(reverseList(reverseList(head)))…);
把冗余逻辑化简后,我们实际只需要传入head即可完成。我们之所以还要在外面嵌套那么多次是因为我们把head->next这个中间量给拿出来了。既然总是要修改返回值。为什么不在返回之前就改好呢?
typedef struct ListNode ListNode;
struct ListNode* reverseList(struct ListNode* head) {
if(head || head->next) return NULL;
ListNode* newhead = reverseList(head->next);
head->next->next = head;
head->next = NULL;
return newhead;
}
这样我们就成功的实现了递归法。刚才动态数组存指针的“傻方法”突然摇身一变蜕变成了”聪明方法“。这也是刚才为什么说思路已经非常接近递归了。空间复杂度为O(n),递归不是不用储存每个节点的指针,而是递归法实现链表反转时,每一次调用 reverse 函数都会创建一个栈帧,这个栈帧中会保存当前处理节点的指针(以及局部变量等上下文),所有递归调用的栈帧累积起来,就保留了链表中每个待处理节点的指针信息。但在实际实践中通常不会使用这种方法,尤其在工程实践中,递归通常会被限制使用,这是为了避免栈溢出(stack overflow)。如果非要使用,可以用动态数组替代。
1.2.3双指针迭代法
绕了这么一大圈,结果我们之前优化空间的目的反而没能实现,甚至比不过头插法的O(1);原因就在于我们是顺着一开始想到的暴力方法优化的。而且,即使是递归法,仍然也是从尾部开始换方向,只不过因为提前保存了前面节点的指针,不会出现重复遍历的问题。对于直接反转指针的操作,我们还没有真正意义上的从头往后去进行尝试。

让我们回到这张图,尝试直接转换看看会发生什么。

二号节点以及之后的节点全部丢失,我们先用tmp(temp)指针保护起来。

这样一来,核心问题就全部暴露无遗。第一,二节点的next能通过tmp->next操控,但是找到一节点依赖头节点,如果是在中间节点,那么为了找前置节点就必须再次遍历。所以必须再加入prev指针来保留前置节点的位置信息。但此时tmp->next仍然未被“解放”。按照我们之前的观点,必须还有个指针分担tmp的重任。索性我们就分别给他们命名为curr(current)和next。

总算可以毫无卡顿的流畅进行反转操作了,从动画效果来看,似乎叫做三指针迭代法更加合理。的确很多人会因为直观而叫做三指针迭代法,但实际上核心指针只有prev和curr两个同速指针长期在场。next虽然在动画中和curr捆绑。但具体落地时,next只是一个临时变量。所以双指针指的是curr和prev,这点切勿混淆。我相信经过之前的几番推演。这个代码的落地对你来说已经是小菜一碟了。
typedef struct ListNode ListNode;
struct ListNode* reverseList(struct ListNode* head){
ListNode* curr = head;//初始指向首元节点
ListNode* prev = NULL;//初始"指向"NULL
while(curr){//curr为NULL就结束,相同速度,在prev前面,不会丢失链表
ListNode* next = curr->next;//临时保护后续的节点
curr->next = prev;//将prev解放出来
prev = curr;//同理
curr = next;//注意不要使用curr->next,已经被我们修改
}
return prev;
}
2.合并两个有序链表-简单


作答接口:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
struct ListNode* mergeTwoLists(struct ListNode* list1, struct ListNode* list2) {
//此处填写代码
}
2.1 题目分析
第一反应:【双指针】 + 【虚拟头节点】 可以秒杀
typedef struct ListNode ListNode;
struct ListNode* mergeTwoLists(struct ListNode* list1, struct ListNode* list2) {
if(!list1) return list2;
if(!list2) return list1;
ListNode dummy;
dummy.next = NULL;
ListNode* prev = &dummy;
while(list1 && list2){
if(list1->val < list2->val){
prev->next = list1;
list1 = list1->next;
}else{
prev->next = list2;
list2 = list2->next;
}
prev = prev->next;
}
prev->next = list1? list1 : list2;
return dummy.next;
}
还存在递归实现的方式,但空间复杂度为O(n+m),迭代法仍是首选。

2.2 思路推导
2.2.1 迭代法(主链实现)

前面之所以铺垫那么多,主要是因为拆解我们切入问题的辩证思考方法,接下来我们就不再嘴碎,开始直接运用。

经此一役,我们意识到仍然是一个串珠子游戏。只不过在其中加入了比大小的要素。比大小需要两个对象才能进行。两个已经排好序的链表合成新的有序链表时,我们可以先从他们的最值进行比较,最值和最值之间才能比出真正的最值出来。而比较的结果只有三种情况:小于、等于、大于。对于排序而言,等于的情况两个对象的先后差异被他们的同质性消解,即仍然存在先和后,比如图中就有颜色的差别。但是对于本题而言没有区别。因此我们需要考虑的就只有小于、大于的二分情况了。
具体怎么实现却让我们感到迷茫。如果你的数学思维不错,能立马意识到对称性,也就只用写小于或大于的其中一份逻辑,另一份采用【对称换元】就能自然形成完美的代码实现,list1长还是list2长?谁的节点插入到谁的链表当中?这些问题统统没有意义,因为都是一样的。
的确对称思想能够绕开弯路,直奔答案。但我们还是从普遍直觉的角度来把路走顺,假设我们完全没有思路的情境,为我们的思维上好底层保险。既然我们一开始不能意识到对称的做法,我们必须先找到一个思考锚点。那我随便找一个作为主链总行吧。list1顺眼,就以它为主链。 找到思考锚点过后,如果只是顺着思路写下去,必然会写出大量冗余代码。这是因为原本自然的逻辑为了给我们的直觉服务而绕了大量弯路,这点在我们推演反转链表的递归实现时就有涉及,我们可以继续顺着逻辑把我们自创的【主链法】推导下去,看看是不是存在大量”逻辑冗余“。

插入到比较数的前面还是后面呢?产生这个疑问大概率是因为将第一个待插入节点插入主链的首元节点时,出现了主链易位的情况,也就是head会跟着动。
如果放在后面,如果原本主链是连续相同的值的例如1、1,我们在1之后插入一个更大的值,1、2、1,显然不行,而且如果副链最小值比主链最小值小呢?

回顾前面,我们很快想到了用哑元节点来解决,同时还需prev接应插入操作,动图只考虑了两表等长的状况,所以还需补上循环后的处理,出循环只可能有两种情况,一是list1 = NULL,二是list2 = NULL,不会出现同时为空指针的情况。list1 = NULL说明list2剩下的节点值都大于list1的最大值,list2 = NULL则说明链表已经完成。我们可以用三目操作符简洁表示。
目前代码如下:
typedef struct ListNode ListNode;
struct ListNode* mergeTwoLists(struct ListNode* list1, struct ListNode* list2) {
if(!list1) return list2;//list1不存在时,无需merge,返回list2
if(!list2) return list1;//同理
ListNode dummy;
dummy.next = list1;//以list1为主链
ListNode* prev = &dummy;
while(list1 && list2){
if(list1->val >= list2->val){
prev->next = list2;
list2 = list2->next;
prev->next->next = list1;
prev = prev->next;//注意,节点插入后,prev和list1隔开了一个节点
}else{
prev = prev->next;
list1 = list1->next;
}
}
prev->next = list1? list1 : list2;//如果list1还存在,说明prev指向的不是尾节点,并且已经全部插入
//不需要额外调整,仍然为list1。如果不存在,就接上list2。
return dummy.next;
}

2.2.2 迭代法(对称实现)
这样,我们还是比较简洁地完成了这道题。但仍然存在逻辑上的冗余:prev->next->next = list1;他的作用在于每次循环都维护原list1的链式结构,如下图所示。这是因为我们思路被锚定在了主链上,我们”害怕“主链的地位易位,因此为了维护主链的正当性,无意识地造成了代码的冗余。通过动画不难注意到,即使我们不走这一步,我们的下一步仍然会比较list1->val与list2->val的大小,这时候就决定了我们指向何处。prev->next->next = list1;相当于提前规划了、内定了主链。但实际上我们要的从来不是一个不变的主链地位,而是最终得到合并后的有序链表。主链可以在过程中被不断切换。因此,dummy.next = list1;的初始化也是没有意义的。

typedef struct ListNode ListNode;
struct ListNode* mergeTwoLists(struct ListNode* list1, struct ListNode* list2) {
if(!list1 || !list2) return list1? list1 : list2;//list1不存在时,无需merge,返回list2
ListNode dummy;
dummy.next = NULL;
ListNode* prev = &dummy;
while(list1 && list2){
if(list1->val >= list2->val){
prev->next = list2;
list2 = list2->next;
}else{
prev->next = list1;
list1 = list1->next;
}
prev = prev->next;
}
prev->next = list1? list1 : list2;//谁还没空就指向谁
return dummy.next;
}
这样就得到了完美的合并逻辑,并且不用注意prev被隔开的特殊情况,逻辑清晰统一,代码简洁好写。

时间复杂度: O(n + m)空间复杂度:O(1)
2.2.3 递归法
从图中可以直观感受到,整个过程更像是在”串珠子“。每次的核心步骤其实只有一个——谁小先指向谁。承接反转链表的递归思路,我们不止可以从头到尾,还可以从尾回头。依靠递归产生的栈帧隐性地”记忆“了每个节点的指针。使其回溯性地从后往前穿,代码实现如下。
typedef struct ListNode ListNode;
struct ListNode* mergeTwoLists(struct ListNode* list1, struct ListNode* list2) {
// 边界条件
if(!list1||!list2) return list1? list1 : list2;
// 递归选择较小的节点,拼接后续结果
if (list1->val <= list2->val) {
list1->next = mergeTwoLists(list1->next, list2);
return list1;
} else {
list2->next = mergeTwoLists(list1, list2->next);
return list2;
}
}
如此一来就把初始的判空逻辑和末尾的判存逻辑完成了统一,逻辑更加清晰优美,但是仍然存在空间开销上的硬伤。
时间复杂度O(n + m)空间复杂度:O(max(n , m)) 最优解仍然是迭代法
3.合并K个升序链表 – 中等


作答接口:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
struct ListNode* mergeKLists(struct ListNode** lists, int listsSize) {
//此处填写代码
}
3.1题目分析
这道题LeetCode官方整合时放在了困难题中,也是链表中少数的困难题,但其实际就算是最优解分支合并法只能到中等难度,只是暴力AC仍然属于简单难度。
时间复杂度 空间复杂度
暴力递归 O(k*n) O(k)
暴力迭代 O(k*n) O(1)
优先队列 O(n*log k) O(k) 动态k时最优解
分治合并(递归式) O(n*log k) O(log k)
分治合并(迭代式) O(n*log k) O(1) 静态k时最优解
第一反应应当是【分治法】和【优先队列】,两种方法的时间复杂度都为O(N * log K)(N为所有和节点总数,K为链表数量)空间复杂度上分治为O(log K),优先队列为O(K),但由于C语言实现小顶堆需要另开篇幅,一般是使用C++自带的STL库解决,而且本文重点讨论链表方法,以及代码简洁性等考虑下,首选【分治法】。此处展示空间复杂度 O(1) 的迭代式分治。
typedef struct ListNode ListNode;
struct ListNode* mergeTwoLists(struct ListNode* list1, struct ListNode* list2) {
if(!list1) return list2;
if(!list2) return list1;
ListNode dummy;
dummy.next = NULL;
ListNode* prev = &dummy;
while(list1 && list2){
if(list1->val < list2->val){
prev->next = list1;
list1 = list1->next;
}else{
prev->next = list2;
list2 = list2->next;
}
prev = prev->next;
}
prev->next = list1? list1 : list2;
return dummy.next;
}
struct ListNode* mergeKLists(struct ListNode** lists, int listsSize) {
if(!listsSize) return NULL;
while(listsSize > 1){
int mergeSize = 0;
for(int i = 0; i < listsSize – (listsSize % 2); i += 2){
lists[mergeSize++] = mergeTwoLists(lists[i],lists[i + 1]);
}
if(listsSize % 2 != 0){
lists[mergeSize++] = lists[listsSize – 1];
}
listsSize = mergeSize;
}
return lists[0];
}
3.2 思路推导
3.2.1 ”暴力串珠法“
经过先前思想的升华,拿到这道题时,你至少不会完全没思路,至少你能想到直接或间接地利用刚才合并两个有序链表的逻辑。但是,最小值的比较不再是简单的二分逻辑,显然我们需要一个新变量来保存当前比较中的最小值。不妨叫做currMin。
另一个问题是,链表的判空也不再轻松,我们很容易想到循环内加入判空逻辑直接跳过空链表。循环的终止逻辑呢?我们没法像之前一样将所有链表的头指针列举出来。这样类似的情境让我们很容易地想到递归,但我们可以暂时保留这个想法,就我们先前的经验,递归必然带来空间上的开销。先看看有没有更好的替代方案。
注意到,这次题目给出了一个新的变量——listSize。也就是说我们可以通过判空的同时减少listSize,当数量减少至0时结束循环。但我们不希望又每次跳过时都减少listSize。如果你想通过增添新的数组来存非空的链表,有了刚才合并两个链表时的思考经验,应该意识到我们借助了listSize这个思考锚点,这样的延续思路很可能含有冗余逻辑,也就是内蕴更本质的方法。
我们不妨思考这样做的弊端是什么,不仅空间复杂度提升至O(k),而且代码也不够简洁优雅。的确,我们不必预设每个算法都是简洁优雅的,在考试、竞赛、面试时,我们也没有功夫去做其他的尝试,但在学习阶段,这种刨根问底的思考却有助于我们形成扎实的知识网络,对思维的提升同样大有裨益,能为我们以后快速作答夯实基础。
我们没必要抛弃现成的数组不用,不如对退出逻辑暂时留空,毕竟我们在未遍历之前是不知道n的也就是总节点个数的。干脆先提炼出核心步骤,稍后再来考虑。
对于串珠子这件事,我们早就不陌生。第一步就是从k组链表各自的第一个元素里中找出最小的,第二步指向它,对应list[i]前进。最暴力的办法就是直接迭代。时间复杂度也就直接导向O(k*n)。
typedef struct ListNode ListNode;
struct ListNode* mergeKLists(struct ListNode** lists, int listsSize) {
ListNode dummy;
dummy.next = NULL;
ListNode* prev = &dummy;
while(1){
int curMin = ?;//待完成
for(int i = 0; i < listsSize; ++i){
if(!lists[i]) continue;
if(lists[i]->val < curMin){
curMin = lists[i]->val;
}
}
prev->next = lists[?];//待完成
prev = prev->next;
if(?) break;//待完成
}
return dummy.next;
}
写到这里,我们一共遇到了三个问题
1.循环退出条件未定
2.最小值如何初始化?
3.最小值对应的lists下标未记录
暂时不管1,下表我们引入minIdx解决。
同时注意到:

我们可以把curMin初始化为100000,当然,这样只是为了做题,你也可以像这样麻烦的去随便找个非空值来初始化。
for(int i = 0; i < listsSize; ++i){
if(!lists[i]) continue;
curMin = lists[i]->val;
minIndex = i;
break;
}
这显然没有必要。在初始化minIdx时我们想到,我们每次操作都必然要找到一个minIdx的值,那么初始化minIdx似乎没有意义,但是这样意味着,如果我们将minIdx初始化为负数,那么我们不久可以通过判断它的正负来判断还有没有非空链表了?这样,退出逻辑也就被我们顺带解决了。
typedef struct ListNode ListNode;
struct ListNode* mergeKLists(struct ListNode** lists, int listsSize) {
if(listsSize == 1) return lists[0];
ListNode dummy;
dummy.next = NULL;
ListNode* prev = &dummy;
while(listsSize > 0){
int curMin = 100000;
int minIdx = -1;
for(int i = 0; i < listsSize; ++i){
if(!lists[i]) continue;
if(lists[i]->val < curMin){
curMin = lists[i]->val;
minIdx = i;
}
}
if(minIdx == -1) break;
prev->next = lists[minIdx];
lists[minIdx] = lists[minIdx]->next;
prev = prev->next;
}
return dummy.next;
}
时间复杂度O(n*k),空间复杂度O(1)

3.2.2 暴力迭代法
不出所料,我们的思考锚定在了”穿珠子“这一个动作上,或许你想说,为什么用这么蠢的办法,明明刚才我们就已经实现了两个有序链表的合并操作,我们可以直接利用它。的确,但这是由于本文的刻意安排,如果你头一次遇到合并有序链表的题就是k组呢?这不是钻牛角尖、思维洁癖,而是的确有价值的思考。
typedef struct ListNode ListNode;
struct ListNode* mergeKLists(struct ListNode** lists, int listsSize) {
if (listsSize <= 0) return NULL;
ListNode* head = lists[0];
for (int i = 1; i < listsSize; ++i) {
head = mergeTwoLists(head, lists[i]);
}
return head;
}
时间复杂度O(k*n),空间复杂度O(1)
由此可见,此题若只是想要拿到AC,是非常简单的一件事,实在有损困难题的脸面(笑)。

3.2.3 优先队列法(最小堆实现)
那么为什么我们写的“暴力串珠法”,和公认的暴力迭代法同为时间复杂度O(k*n),经过多次测验,却是暴力迭代法稳定得快呢?不妨以k = 10^4,每个链表 500 个节点为例,计算一下。



而且,越是链表数相对更大,链表节点数相对更小的情况,暴力迭代的重复遍历(每次合并两个链表之后,新链表的每个已经被遍历过的节点在和下个链表合并时又被重复遍历一次)的公差就越小,劣势就越不明显。而”暴力串珠法“找到实际最小值时,我们找出第一次最小值过后,就往了其他数之间的大小关系,为了那更新的一个数,又重新遍历了一次。那我们优化的方向就转变为优化重复找最小值的过程。这里就引出了贪心算法(优先队列)。我们先看下面这个情境:

现有一百颗桃子。猴爷爷只让猴子吃一个桃,猴子是个急性子,既想要吃最大的桃,又想要最快比对出哪个桃子最大。只计分辨桃子大小的时间,他应该怎么做能最快找到最大的桃子呢?
没错,我们刚才的思路就是让猴子拿着它见到的最大桃一直和下一个比对,直到见过全部的桃子。总共比对了99次。这也的确是理论上的最优解。但合并k组链表的情况也是如此吗?并不是,急猴子摘桃的情景中,猴子每次比对挑出最大的桃过后,就只剩99颗桃了。这是一个静态的过程,那如果猴子吃完还想吃最大的桃子呢?它又得要挑98次。而且,猴子挑桃是越挑越少,而我们挑最小值后,如果被挑链表没有空,每次要挑的总数仍然不变。这就像每次猴子挑完一个最大桃之后,又会它拿桃的位置补上一个和刚才一样大或者比刚才小的桃子。这是一个动态的过程,会不断有桃子补充进来。这个时候遍历所有桃子就不再是最优解,即便静态,如果急猴子想要按从大到小的顺序吃完,直接遍历也绝不会是最优解,。这正是我们的”暴力串珠法“慢的真正原因。
既然问题出现在没有记忆上,那我们只要记住拿走的数对应的下标还有第二名下标,判断新增数和刚才最小值是否相等,若相等,就直接取这个数,否则就与第二名进行比较,拿走更小值。这样,我们的确完成了一定程度的优化,省去了部分重复次数。但时间复杂度仍然为O(k*n)。因为我们在用过了第二名之后,又得重新遍历一次,找出第一名和第二名出来。既然这么费事,我们干脆用一个容器把这个顺序暂时存起来。这样起码会有O(k)的空间复杂度。我可以直接告诉大家结论,这个优化方向就是【优先队列】的小根堆实现。但由于涉及二叉树、堆排序,且接下来还需介绍分治思想,本文重点讨论链表范围,至此也有11794字,就留给以后有机会再来聊聊了。
3.2.4 分治合并法(迭代实现-自底向上)
我们暂时放下优化”暴力串珠法“来思考暴力迭代法如何优化,先看这张图。

从图中我们就能直观感受到这种暴力方法的无力,这还只是5组链表。看到这张图时,不知你是否会下意识想要地多用几个dummy节点去把这些”散开的拉链“拉好。直觉告诉我们,这种方法一定效率比一个一个合要高得多。直觉很多时候并不可靠,我们可以尝试建立数学模型,如果这个直觉准确,那么最后肯定能得到一个不等式。

这是【矩阵链乘法代价不等式】(Matrix Chain Multiplication Cost Inequality)的一种变形。也是归并排序效率高于冒泡/插入排序的抽象本质。
仅需了解,和我们做题完全没有关系,我们只需要根据直觉继续优化即可。很容易想到这样一种递归的实现方式:我们将第一组两个合并之后,剩下那些链表还要我们继续合并,在我们看来,他们就是另外一堆k组链表。实现了单元步骤之后就能直接通过大结构拆成小的相同结构的逻辑,直接通过递归实现。
typedef struct ListNode ListNode;
struct ListNode* mergeKLists(struct ListNode** lists, int listsSize) {
if(listsSize == 0) return NULL;
if(listsSize <= 1) return lists[0];
int mergeSize = 0;
for(int i = 0; i < listsSize; i += 2){
if (i + 1 <= listsSize – 1) {
lists[mergeSize++] = mergeTwoLists(lists[i], lists[i + 1]);
}else{
lists[mergeSize++] = lists[i];
}
}
return mergeKLists(lists,mergeSize);
}

时间复杂度O(n*log k ),空间复杂度O(log k),但这并非递归,严格来说仍然是【自底向上的迭代式分治】 ,叫迭代式是因为这个思路的空间复杂度跟以往我们借助栈帧的情况不同。是我们为了代码简洁出现的,我们完全可以优化它。
typedef struct ListNode ListNode;
struct ListNode* mergeKLists(struct ListNode** lists, int listsSize) {
if(listsSize == 0) return NULL;
while(listsSize > 1){
int mergeSize = 0;
for(int i = 0; i < listsSize; i += 2){
if (i + 1 <= listsSize – 1) {
lists[mergeSize++] = mergeTwoLists(lists[i], lists[i + 1]);
}else{
lists[mergeSize++] = lists[i];
}
}
listsSize = mergeSize;
}
return lists[0];
}
时间复杂度O(n*log k),空间复杂度O(1)。
3.2.5分治合并法(递归实现-自顶向下)
之所以称之为自底向上,是因为我们将k组两两合并的过程将底部分为两两一组。即为分治,然后逐渐合并成一个链表,即为合并。这也就是分治合并法的精髓

你可能会想,自底向上好理解,可是自顶向下又是怎么回事,这个顶不正是我们的目标吗?说得好,如果只是排序一个链表的话,我们自顶向下地拆分,再合并。也就是归并排序,这正是自顶向下的最好体现。但并在这不是不能使用自顶向下。这非是一个顺序问题,还记得我们在解决反转链表时,从头到尾和从尾到头的两种情况吗。我们一开始通过从尾到头,发现了可以用动态数组存下指针,进而发现了递归的本质作用。并且实际情况递归是延迟操作,当终止条件触发时,再回溯性地开始操作。后来我们通过强行顺向遍历发现了双指针迭代法。这种感觉是不是非常相似?没错。我们仍然可以利用递归。用和归并类似的方法来自顶向下进行二分。
二分同样需要处理奇数长度的问题,所以引入变量left、mid、right。为了递归,通常我们会写一个辅助函数helper方便二分下标,因为作答接口的参数不支持我们传入递归更新参数。
typedef struct ListNode ListNode;
ListNode* mergeKListsHelper(ListNode** lists,int left,int right){
if(left > right) return NULL;
if(left == right) return lists[left];
int mid = (left+right) / 2;
ListNode* leftList = mergeKListsHelper(lists, left, mid);
ListNode* rightList = mergeKListsHelper(lists, mid + 1, right);
return mergeTwoLists(leftList,rightList);
}
struct ListNode* mergeKLists(struct ListNode** lists, int listsSize) {
if(listsSize == 0) return NULL;
return mergeKListsHelper(lists,0,listsSize – 1);
}

三、总结
至此,除了优先队列的方法由因篇幅和重点限制为展开以及暴力递归略去不讲以外。我们已经通过摸清这三道题的所有方法,接下来就让AI总结一下:
本文通过 LeetCode 206.反转链表、21.合并两个有序链表、23.合并K个升序链表三道由浅入深的题目,拆解了链表题的解题逻辑、优化路径,核心不仅是掌握具体题解,更在于搭建“从直觉思路到最优解法”的辩证思考框架,形成可复用的算法解题思维,以下是核心总结。
1. 核心题型与解题方法梳理
三道题目覆盖链表基础操作、双指针应用、分治思想等核心考点,每种题型均经历“暴力思路→逐步优化→最优解法”的推导,具体可归纳为:
1.1 反转链表(LeetCode 206)
核心考点:指针方向调整、节点遍历与保护,核心目标是实现“原地反转”以优化空间开销。
-
思路演进:从“尾到头读取重建链表”的暴力思路(O(n²)时间、O(n)空间),逐步优化为正向遍历的头插法,最终落地双指针迭代法,实现时间O(n)、空间O(1)的最优解;同时衍生出递归法,虽逻辑简洁但存在栈溢出风险(空间O(n)),工程中不推荐使用。
-
关键突破:通过临时指针保护后续节点,避免指针反转时链表断裂;双指针(prev/curr)的核心是“同速遍历、分步反转”,next仅作为临时变量,厘清“双指针”的定义边界,避免混淆三指针概念。
-
核心方法:双指针迭代法(最优)、头插法(逻辑直观)、递归法(思维拓展)。
1.2 合并两个有序链表(LeetCode 21)
核心考点:有序结构的遍历对比、链表拼接,核心目标是简化逻辑、避免冗余操作。
-
思路演进:从“指定主链插入副链”的直觉思路(存在主链维护的冗余逻辑),优化为“对称对比”的迭代法,借助虚拟头节点(哑元节点)解决头指针易位问题,统一空表与非空表的操作逻辑。
-
关键突破:摒弃“主链思维”,采用“谁小先指向谁”的对称逻辑,简化条件判断;虚拟头节点的灵活运用,避免单独处理头节点插入的边界情况,降低代码复杂度。
-
核心方法:双指针+虚拟头节点(最优,O(n+m)时间、O(1)空间)、递归法(逻辑优美但空间O(max(n,m)))。
1.3 合并K个升序链表(LeetCode 23)
核心考点:多结构融合、贪心思想/分治思想应用,核心目标是优化“最小值查找”的效率,降低时间复杂度。
-
思路演进:从“暴力串珠法”(逐一遍历找最小值,O(kn)时间)、“两两迭代合并”(O(kn)时间),逐步优化为分治合并法,借助“合并两个有序链表”的基础逻辑,将问题拆解为子问题递归/迭代求解,实现时间复杂度优化至O(nlogk)。
-
关键突破:利用分治思想减少重复遍历,将K个链表的合并拆解为logk次“两两合并”,规避暴力方法中重复比对的冗余;同时可通过优先队列(小根堆)维护最小值,适配动态K的场景(空间O(k))。
-
核心方法:迭代式分治(最优,O(nlogk)时间、O(1)空间)、递归式分治(O(nlogk)时间、O(logk)空间)、优先队列(动态场景适配)、暴力法(仅用于AC兜底)。
2. 通用解题思维与优化技巧
三道题目虽场景不同,但解题逻辑与优化路径具有高度通用性,可提炼为以下4点核心思维,适配各类链表题:
2.1 边界处理优先
链表题的核心易错点的是边界情况,解题时需优先处理空表、单节点链表、链表长度不一致等场景,借助虚拟头节点、提前判空等操作,统一解题逻辑,避免冗余的条件判断。例如合并链表时先判断“任一链表为空则返回另一链表”,反转链表时处理“头节点为NULL”的情况。
2.2 指针管理是核心
链表的离散存储特性决定了“指针保护”的重要性:遍历或修改指针方向时,需提前用临时指针保存后续节点地址,避免链表断裂(如反转链表中用next保存curr->next);同时合理使用双指针(同速、异速),简化遍历与对比逻辑,降低时间复杂度。
2.3 暴力思路是优化的起点
面对陌生链表题,无需一开始追求最优解,可先从直觉性的暴力思路入手(如重建链表、逐一遍历),再分析暴力思路的弊端(时间冗余、空间浪费),针对性优化:时间冗余则优化遍历次数(如分治减少重复比对),空间浪费则追求原地操作(如双指针反转替代递归),逐步推导至最优解。
2.4 复用基础逻辑,拆解复杂问题
复杂链表题往往可拆解为基础操作的组合:合并K个链表的核心是复用“合并两个链表”的逻辑,分治思想的本质是“大问题拆解为小问题”;反转链表的递归法与迭代法,本质是“从尾到头”与“从头到尾”的思路互补。掌握基础操作(插入、反转、合并),是解决复杂链表题的前提。
3.方法抉择与场景适配
解题时需根据场景选择合适的方法,兼顾效率与代码可读性,具体适配原则如下:
-
空间优先场景:优先选择迭代法(双指针、迭代式分治),避免递归或额外数据结构(如数组、堆)带来的空间开销,例如工程场景中优先使用双指针反转链表、迭代式分治合并K个链表。
-
代码简洁优先场景:可选择递归法(如合并两个链表的递归实现),但需注意链表长度,避免栈溢出。
-
动态场景(K变化):合并K个链表时,优先选择优先队列(小根堆),无需提前确定K的固定值,适配动态新增/删除链表的场景;静态K则优先迭代式分治,空间开销更优。
-
兜底AC场景:时间紧张时,可先用暴力法(如两两迭代合并K个链表)快速AC,后续再优化至最优解。
4.学习收获与后续延伸
4.1 核心收获
本文的核心价值并非掌握三道题的具体代码,而是搭建“问题拆解→思路优化→方法落地”的通用框架:面对陌生算法题,不再无从下手,而是从直觉思路出发,通过分析弊端、复用基础逻辑、运用算法思想(分治、贪心),逐步优化至最优解;同时深刻理解链表的核心特性,掌握虚拟头节点、双指针、分治等高频技巧,这些技巧可迁移至链表排序、环形链表判断等各类链表题型。
4.2 后续延伸
本次未展开的优先队列(小根堆)实现合并K个链表,可结合二叉树、堆排序知识点补充学习,适配更多动态最值查找场景;同时可拓展练习链表的进阶题型(如环形链表、链表相交、复杂链表的复制),强化指针管理与边界处理能力,进一步巩固链表解题思维。
综上,链表题的解题关键的是“理清指针关系、简化逻辑冗余、复用基础操作”,多画图、多推演指针移动过程,才能突破思维瓶颈,从“会做题”转变为“会拆解题”,真正掌握算法解题的核心能力。
四、结语
历时三天,终于将这第一篇博客肝出来了,作为大一在读学生,我认为我更能从初学者的角度去思考问题。而在这样手把手讲解思路的过程中,我自身同样收获颇丰,原本我自以为早已理解通透的内容,但在讲述时却时常出现卡壳,写不下去的情况。这时候就只能通过查找资料等方式来打通理解。同时也学会了自己制作gif动图来帮助理解。其实创作初衷是在我思考和解决问题的习惯,我很享受讲问题吃透的自洽感。但实际上我们也要区分这种思考的适用情况。这也是为什么我会在体感分析时安排一个实战部分告诉大家并不是必须每次都这样思考。而是这样看似效率低的思考,能将基础不断夯实,有些东西想通了就是一劳永逸,之后思考题目之后越来越快。这也是本文想要传达的核心思想。
在此衷心感谢每个认真阅读完的读者!【约21470字】
个人主页:Elainalz https://blog.csdn.net/2401_86691452?spm=1011.2266.3001.5343
https://blog.csdn.net/2401_86691452?spm=1011.2266.3001.5343
 网硕互联帮助中心
网硕互联帮助中心



评论前必须登录!
注册