从0实现一个简单的线性回归模型（理论篇）

首先我们先说原理 简单来说就是我们预先知道两批数据X，Y, 我们并不知道X，Y之间有着怎样的关系，可能是线性，可能是非线性，或者更复杂的关系，我们需要猜测一个可能的关系进行尝试，尝试不可能一下就试对，我们要做的就是在尝试的过程中进行一步步优化，最终找到X，Y之间的关系。其实本质就是找函数F（X）= Y      即  y = w₁x₁ + w₂x₂ + … + wₙxₙ + b

如下图，X，Y存在线性关系  这里有一个常见的误区就是 我以为是求X，Y。但其实X，Y 是已知的我们要求的是y=wx+b中的参数w和b，而非数据。在线性模型中w表示weight（权重），b表示bias(偏差)。

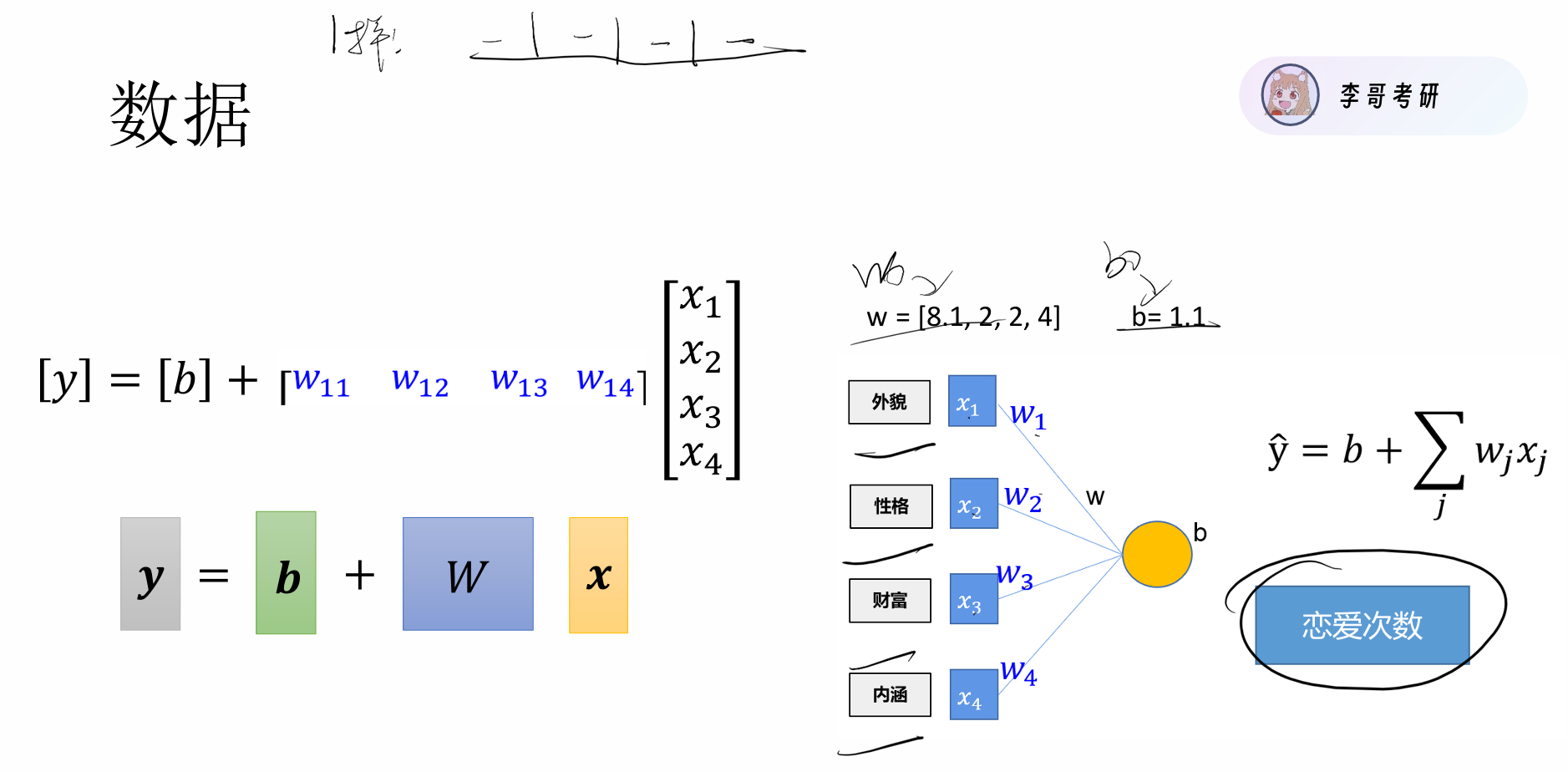
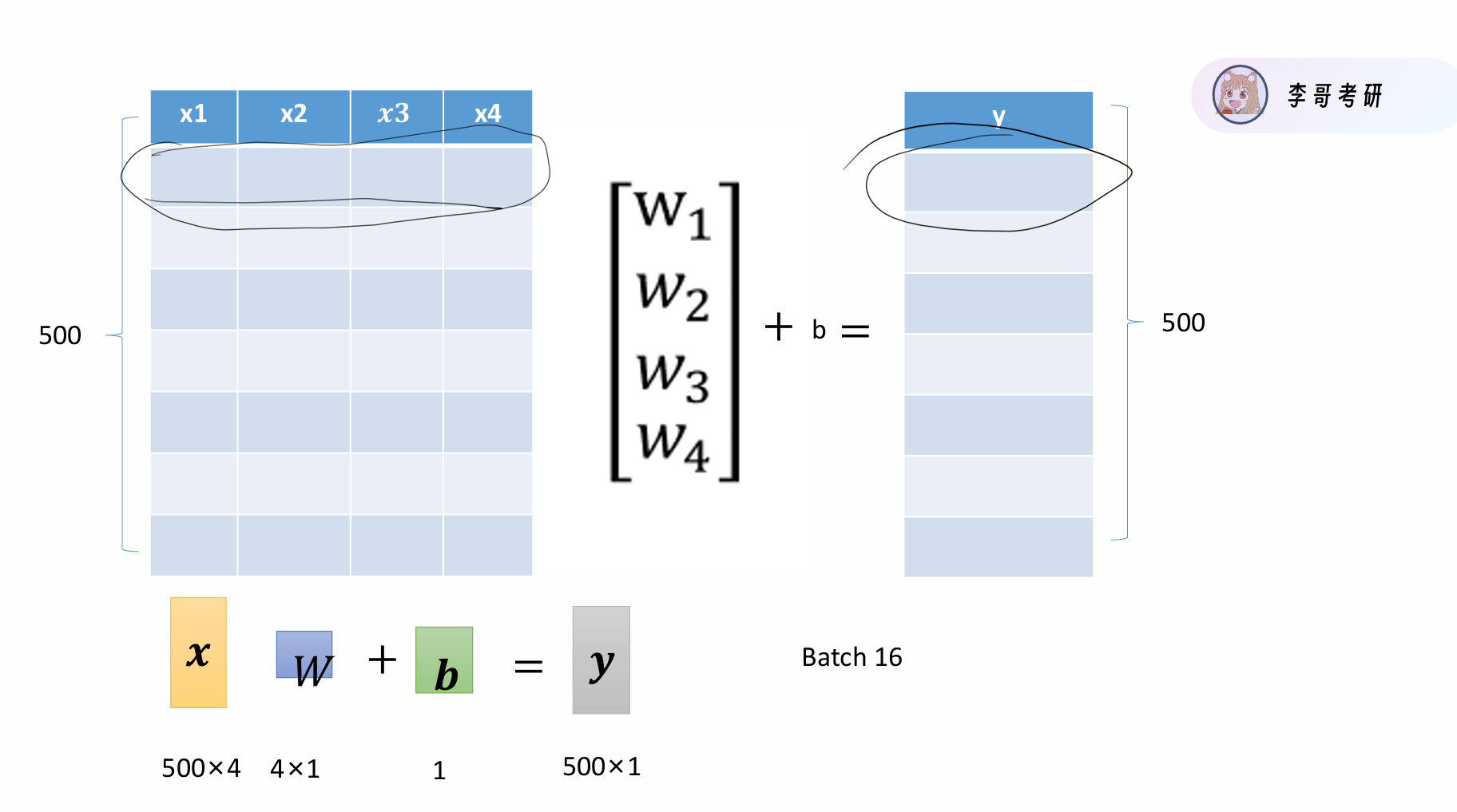
那我们如何找到这个所谓的函数的最优参数呢，具体做法就是我们先给定一个猜测值w,b ，根据这个猜测值代入函数来求出预测值ŷ（这个过程叫做前向传播）,于是得出损失函数

loss = 1/n * Σ|ŷᵢ – yᵢ|，它用来判断我们这一组参数取的怎么样，从公式中也可以看出，loss越小说明我们的参数越好，

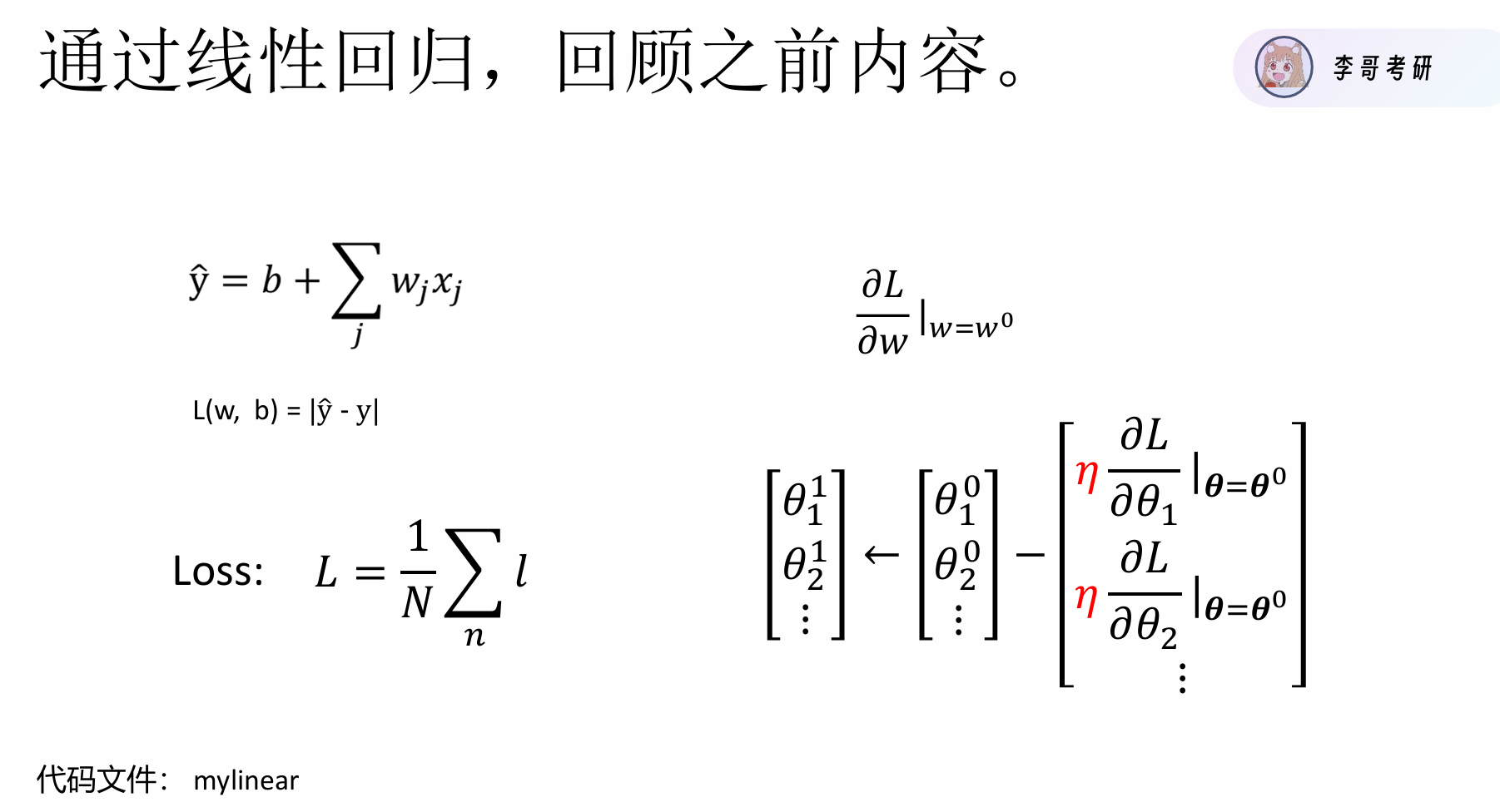
参数肯定不是一试就出来的，仅仅知道"好不好"不够，我们需要知道"怎么改进"。那我们如何都参数进行优化呢，这就引出了大名鼎鼎的反向传播算法。

反向传播计算损失函数对每个参数的梯度（导数）：

• ∂loss/∂w：损失对权重w的偏导数

• ∂loss/∂b：损失对偏置b的偏导数

梯度告诉我们：每个参数应该增加还是减少，以及调整的紧迫程度。

沿着负梯度方向更新参数（因为负梯度是下降最快的方向）：

w_new = w_old – η × ∂loss/∂w b_new = b_old – η × ∂loss/∂b

，

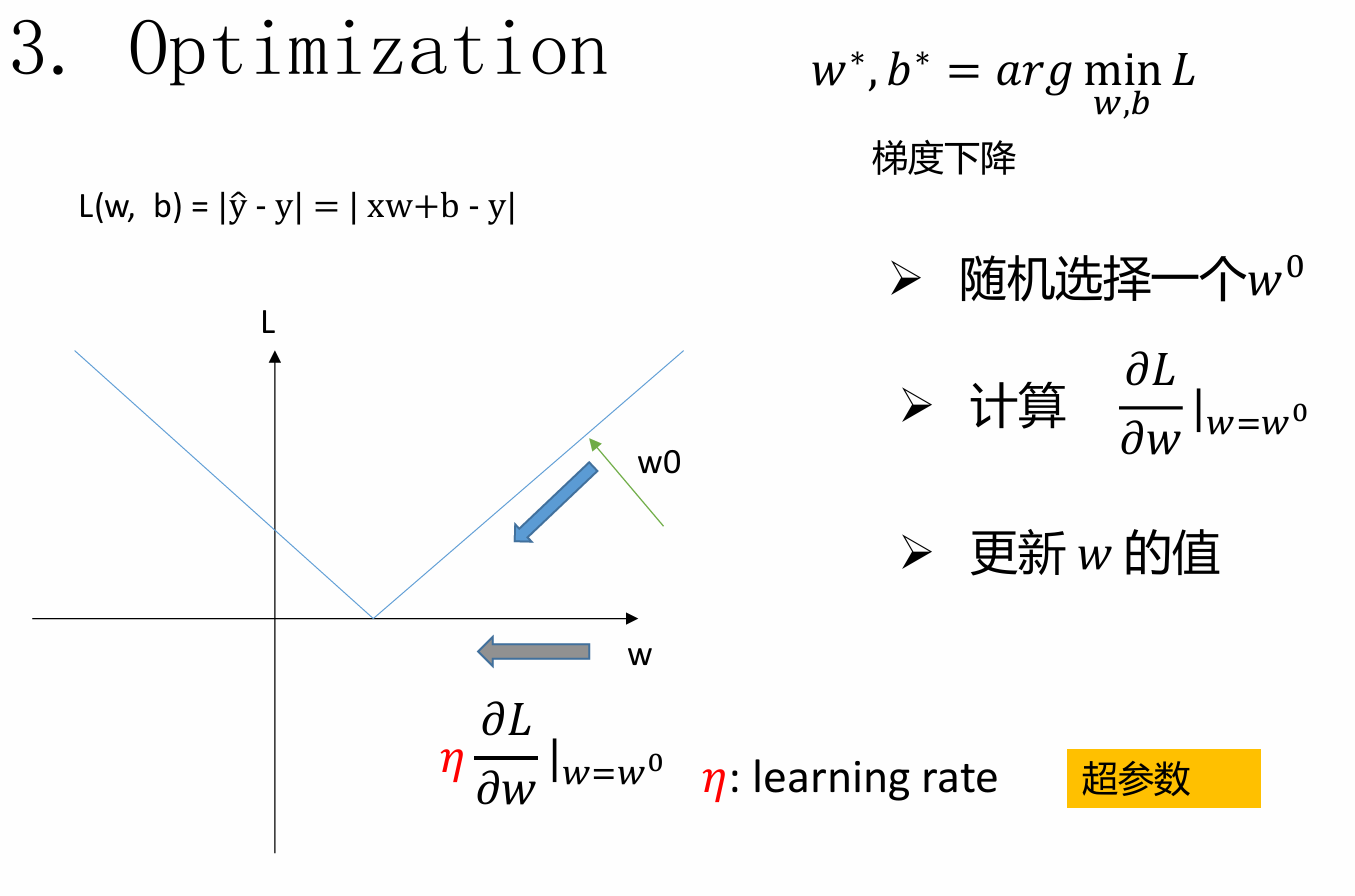
举一个通俗的例子，一个盲人下山，他现在站在山上某一个位置（这就是我们初始给定的w,b），他用脚感受坡度（梯度），往最陡的下坡方向走，一点一点探到最低点。 

learning rate（学习率）代表每次参数更新的步长大小。

在梯度下降算法中，我们通过以下方式更新参数： 参数 = 参数 – learning_rate * 梯度  其中，梯度指明了损失函数下降的方向，而学习率则决定了我们沿着这个方向走多远。

学习率的作用：

步长控制：学习率决定了每次参数更新的大小。较大的学习率意味着更大的步长，可能导致快速收敛，但也可能越过最优点；较小的学习率意味着更小的步长，收敛速度慢，但可能更精确。

收敛性：学习率过大可能导致无法收敛，甚至发散；学习率过小则可能导致收敛速度过慢，或者陷入局部最优点。

训练稳定性：合适的学习率可以使训练过程稳定，损失函数平稳下降。

——–分割线—–

最后总结一下

核心问题：当我们已知数据X和Y，但不知道它们之间的具体关系时，如何找到能够描述这种关系的函数？

关键认识：我们不是要求X和Y（它们已知），而是要求函数中的参数。在线性回归中，这个函数形式为 y = w·x + b，我们需要找到最优的权重w和偏置b。

如何找到这个函数的最优参数呢？机器学习通过梯度下降算法来解决这个问题。具体流程如下：

这个过程中，损失函数是指导方向的"灯塔"，loss越小表示预测越准；梯度是具体的"调整指南"，告诉每个参数应该增减多少；学习率η控制"调整幅度"，避免一次调整过大或过小。

通过这样不断"预测→评估→调整"的循环，模型逐渐从随机猜测进化到准确预测，最终学会数据中的隐含规律。