题目链接 https://kamacoder.com/problempage.php?pid=1044
【题目描述】
在一个城市区域内,被划分成了n * m个连续的区块,每个区块都拥有不同的权值,代表着其土地价值。目前,有两家开发公司,A 公司和 B 公司,希望购买这个城市区域的土地。
现在,需要将这个城市区域的所有区块分配给 A 公司和 B 公司。
然而,由于城市规划的限制,只允许将区域按横向或纵向划分成两个子区域,而且每个子区域都必须包含一个或多个区块。
为了确保公平竞争,你需要找到一种分配方式,使得 A 公司和 B 公司各自的子区域内的土地总价值之差最小。
注意:区块不可再分。
【输入描述】
第一行输入两个正整数,代表 n 和 m。
接下来的 n 行,每行输出 m 个正整数。
【输出描述】
请输出一个整数,代表两个子区域内土地总价值之间的最小差距。
【输入示例】
3 3
1 2 3
2 1 3
1 2 3
【输出示例】
0
【提示信息】
如果将区域按照如下方式划分:
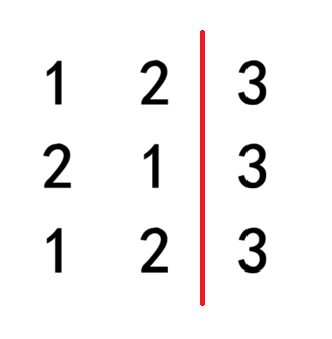
两个子区域内土地总价值之间的最小差距可以达到 0。
【数据范围】
- 1 <= n, m <= 100;
- n 和 m 不同时为 1。
小萌新的刷题笔记~
刚开始看此题,说实话一点都不知道在说什么,没理解意思。思考之后发现:
- 划分方式就是①“一刀切”②只能横着切或者竖着切。
- 分成两个区域之后,分别计算两个区域的价值(就是位置上的数字)的总和,计算差值。
下面我将用例子解释分析:
设n=3, m=4
输入矩阵为:
1 2 3 4
2 1 1 1
1 2 3 1
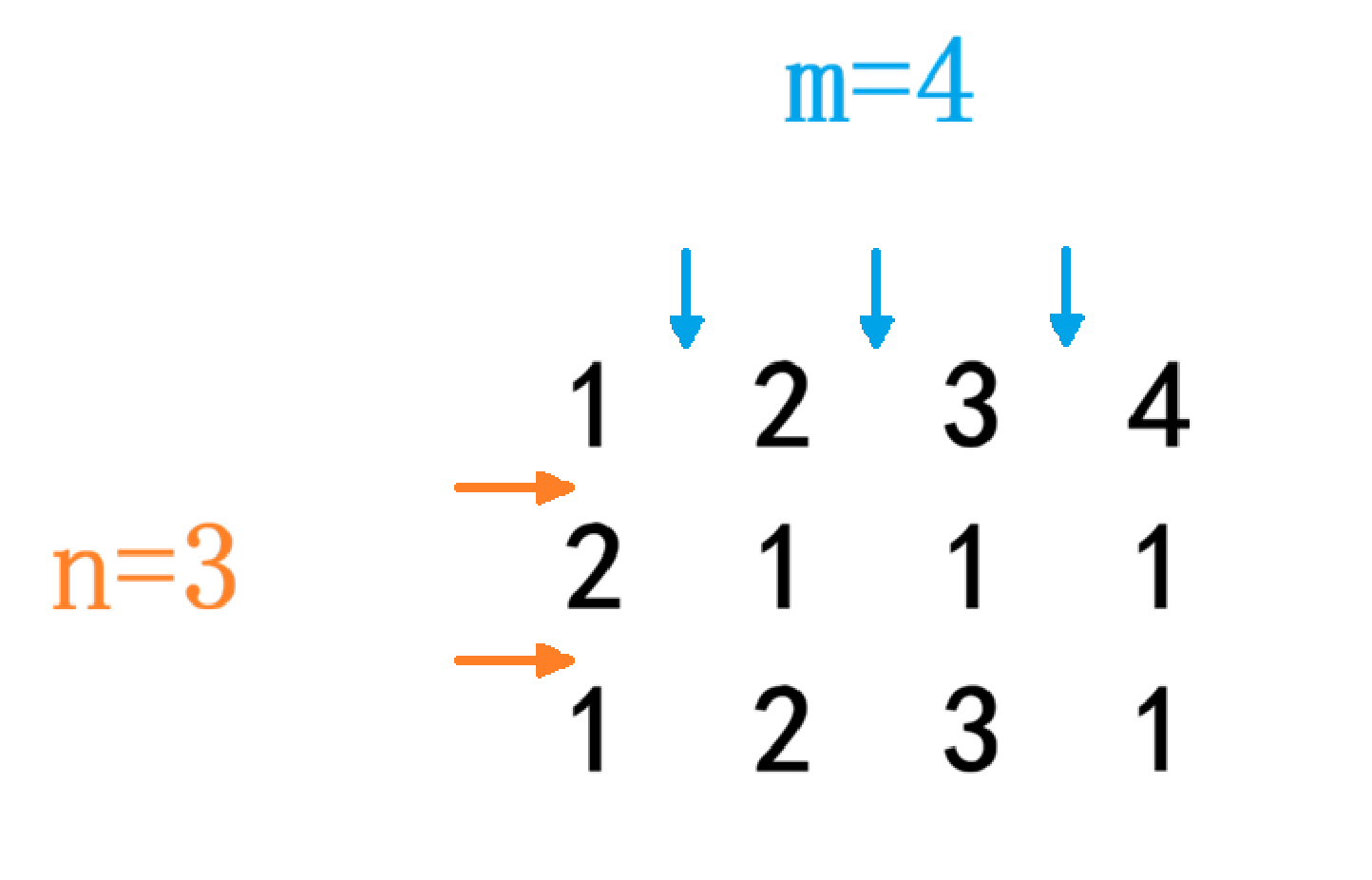
可以看到,横着切(橙色箭头),有 2 个空隙;竖着切(蓝色箭头),有 3 个空隙。如果我这么切:
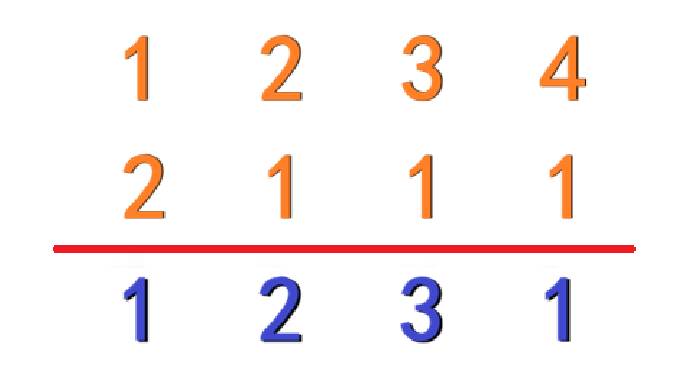
上面橙色的部分给A公司,下面蓝色的部分给B公司(实际上给谁无所谓都可以)。
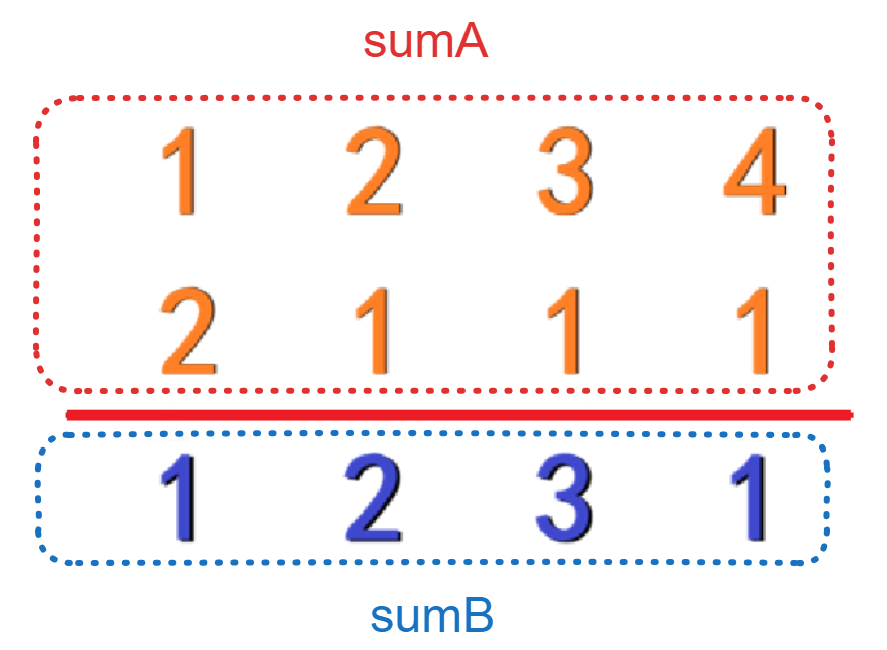
那么A公司的土地总价值就是sumA,即上面的部分加起来;B公司的土地总价值就是sumB,即下面的部分加起来。差值就是 |sumA-sumB| 。
那么接下来,我们要做的,就是遍历所有的划分情况,找到最小差值。如果每一次都一个一个加每个位置的价值,太冗余了,重复的次数非常多。为了解决这一问题,我们把矩阵每一行,每一列的和先计算好,分别存储在数组中:
int sumRow[]=new int[n];//每一行的总和
int sumLine[]=new int[m];//每一列的总和
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
{
arr[i][j]=sc.nextInt();//arr存储矩阵的值
sumRow[i]+=arr[i][j];
}
}
for(int j=0;j<m;j++)
{
for(int i=0;i<n;i++)
{
sumLine[j]+=arr[i][j];
}
}
我们知道,由于一刀切,所有的情况不过于A公司有 前i列 或 前i行 土地,B公司有剩下的土地,自然而然我们想到了前缀和的方法,计算前i行(列)的前缀和。
//求sumRow的前缀和
int sumRowPre[]=new int [n+1];
sumRowPre[0]=0;//初始化
for (int i = 0; i < n; i++) {
sumRowPre[i+1]=sumRowPre[i]+sumRow[i];
}
//求sumLine的前缀和
int sumLinePre[]=new int [m+1];
sumLinePre[0]=0;//初始化
for (int i = 0; i < m; i++) {
sumLinePre[i+1]=sumLinePre[i]+sumLine[i];
}
接下来,我们遍历每一种横切和纵切的情况:
将最小值min初始化为很大的数Integer.MAX_VALUE,计算sumA后,sumB即为总和减去sumA,差距的计算即sumA-sumB的绝对值,利用Math.min方法得到最小的差距。
int min=Integer.MAX_VALUE;
int gap=0;//差距
int sumA=0,sumB=0;
//遍历横切
for(int i=1;i<=n-1;i++)
{
sumA=sumRowPre[i];
sumB=sumRowPre[n]-sumRowPre[i];
gap=Math.abs(sumA-sumB);
min=Math.min(min,gap);
}
//遍历纵切
for(int j=1;j<=m-1;j++)
{
sumA=sumLinePre[j];
sumB=sumLinePre[m]-sumLinePre[j];
gap=Math.abs(sumA-sumB);
min=Math.min(min,gap);
}
具体的完整解释如下:
这段代码的主要功能是处理一个矩阵,目标是找到一种切割方式(横向或纵向),使得将矩阵分成两部分后,两部分元素总和的差值达到最小。代码首先读取矩阵的行数 n 和列数 m,并创建一个相应的二维数组 arr 来存储矩阵元素。在读取输入数据的过程中,代码同时计算了每一行的总和,存储在 sumRow 数组中。随后,通过构建 sumRow 的前缀和数组 sumRowPre,可以快速获取任意连续行的总和,这是通过初始化一个长度为 n+1 的数组,并递推计算每个位置之前所有行总和实现的。
接着,代码通过双层循环计算每一列的总和,存储在 sumLine 数组中。这里的外层循环遍历列,内层循环遍历行,累加同一列的所有元素。同样地,为列总和构建了前缀和数组 sumLinePre,长度为 m+1,以便快速获取任意连续列的总和。在得到行列的前缀和后,代码初始化最小差值 min 为整型最大值,然后遍历所有可能的横向切割位置(从第一行后到倒数第二行后),利用前缀和计算上下两部分的总和并求差值的绝对值,更新最小值。同理,遍历所有纵向切割位置(从第一列后到倒数第二列后),计算左右两部分的总和差值并更新最小值。最终,输出所有切割方式中得到的最小差值,从而实现了高效求解矩阵分割问题。整个算法通过前缀和技巧避免了重复计算,将时间复杂度优化为 O(n+m)。
最终代码如下:
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
int n,m;
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
int arr[][]=new int[n][m];
int sumRow[]=new int[n];//每一行的总和
int sumLine[]=new int[m];//每一列的总和
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
{
arr[i][j]=sc.nextInt();
sumRow[i]+=arr[i][j];
}
}
//求sumRow的前缀和
int sumRowPre[]=new int [n+1];
sumRowPre[0]=0;//初始化
for (int i = 0; i < n; i++) {
sumRowPre[i+1]=sumRowPre[i]+sumRow[i];
}
for(int j=0;j<m;j++)
{
for(int i=0;i<n;i++)
{
sumLine[j]+=arr[i][j];
}
}
//求sumLine的前缀和
int sumLinePre[]=new int [m+1];
sumLinePre[0]=0;//初始化
for (int i = 0; i < m; i++) {
sumLinePre[i+1]=sumLinePre[i]+sumLine[i];
}
int min=Integer.MAX_VALUE;
int gap=0;//差距
int sumA=0,sumB=0;
//遍历横切
for(int i=1;i<=n-1;i++)
{
sumA=sumRowPre[i];
sumB=sumRowPre[n]-sumRowPre[i];
gap=Math.abs(sumA-sumB);
min=Math.min(min,gap);
}
//遍历纵切
for(int j=1;j<=m-1;j++)
{
sumA=sumLinePre[j];
sumB=sumLinePre[m]-sumLinePre[j];
gap=Math.abs(sumA-sumB);
min=Math.min(min,gap);
}
System.out.println(min);
}
}
 网硕互联帮助中心
网硕互联帮助中心





评论前必须登录!
注册