网硕互联帮助中心一、CKF的定位与核心思想
CKF是一种用于非线性系统状态估计的递推贝叶斯滤波算法。要理解它，我们需要从经典的卡尔曼滤波谈起。
卡尔曼滤波：是线性高斯系统状态估计的最优解。它假设系统模型（状态转移和观测模型）都是线性的，并且过程噪声和观测噪声都是高斯白噪声。
非线性挑战：现实中绝大多数系统（如飞行器姿态、目标跟踪、金融模型）都是非线性的。直接应用KF会失效。
EKF的解决方案：扩展卡尔曼滤波通过一阶泰勒展开在估计点处线性化非线性函数，然后应用标准KF公式。缺点：线性化误差大，可能导致滤波发散；需要计算复杂的雅可比矩阵。
UKF的解决方案：无迹卡尔曼滤波采用确定性采样策略。它选取一组“Sigma点”来捕获状态分布的均值和协方差，将这些点通过非线性函数传播，再重新计算传播后点的统计特性。优点：精度通常高于EKF，无需计算雅可比矩阵。
CKF的核心思想： CKF与UKF类似，也是一种基于确定性采样的非线性滤波方法。但其理论基础完全不同。CKF的出发点是：非线性滤波的核心难点在于计算非线性变换下的高斯加权积分（期望和协方差）。CKF利用球面-径向容积规则，以数值积分的最优方式（在三阶精度内）来近似这些积分。它生成一组数量最少、权重相等的容积点，通过这些点的传播来精确估计后验分布的均值和协方差。
简单比喻：
-
EKF：用一个切平面（线性）来近似一个曲面（非线性）。
-
UKF：用一组精心挑选的、有不同权重的“代表点”去探测曲面。
-
CKF：用一组完全对称、权重相等的“容积点”，按照一个最优的几何规则去探测曲面，能更结构化、更数值稳定地计算曲面下的“体积”（即统计特性）。
二、数学原理：容积规则
这是CKF区别于UKF的理论核心。问题归结为计算如下形式的多维积分：
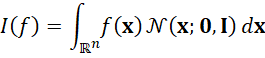
其中，
是标准高斯分布。在滤波中，
是非线性函数。
球面-径向容积规则 将这个积分分解为径向积分和球面积分
评论前必须登录！
注册