【PyTorch入门】手把手带你搭建第一个神经网络（参数计算详解+代码实战）

一、如何从零“搭建”一个神经网络？

大家好，很多初学者在入门深度学习时，常常会对“如何从零开始搭建一个神经网络”感到困惑。别担心，今天这篇文章将手把手带你用 PyTorch 完成这个过程，不仅教你“怎么做”，更让你明白“为什么这么做”。

在 PyTorch 中，搭建一个神经网络就像搭积木一样简单，我们只需要将各种“层”（Layers）堆叠起来。整个过程主要围绕着一个核心类 nn.Module 来展开，我们需要做两件事：

接下来，我们就以一个具体的例子，来构建下面这个简单的三层神经网络模型。

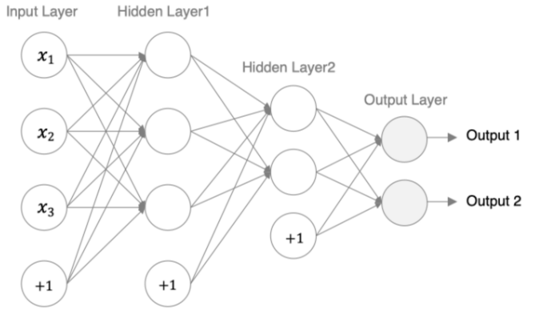
我们的设计要求如下：

• 输入层：接收3个特征。
• 第1个隐藏层：3个神经元，权重采用 Xavier 初始化，激活函数使用 Sigmoid。
• 第2个隐藏层：2个神经元，权重采用 Kaiming (He) 初始化，激活函数采用 ReLU。
• 输出层：2个神经元，因为是多分类任务，最后使用 Softmax 进行归一化。

二、搭建神经网络模型（PyTorch代码实战）

我们先来编写模型的核心代码。这里我们创建一个 Model 类，它继承自 nn.Module。

1. 构造神经网络模型

import torch
import torch.nn as nn
# torchsummary 用于计算模型参数量和查看模型结构, 需要先安装
# pip install torchsummary -i https://mirrors.aliyun.com/pypi/simple/
from torchsummary import summary

# 1. 创建神经网络模型类
class Model(nn.Module):
# 初始化网络结构
def __init__(self):
# 调用父类的初始化方法，这是必须的步骤，确保nn.Module的功能被正确继承
super(Model, self).__init__()

# — 定义网络中的“积木”（各个层） —
# 第一个隐藏层: 3个输入特征 -> 3个输出特征
self.linear1 = nn.Linear(3, 3)
# 第二个隐藏层: 3个输入特征 -> 2个输出特征
self.linear2 = nn.Linear(3, 2)
# 输出层: 2个输入特征 -> 2个输出特征 (对应2个类别)
self.out = nn.Linear(2, 2)

# — 对“积木”的参数进行初始化 —
# 对第一个隐藏层的权重使用 Xavier 初始化，偏置初始化为0
nn.init.xavier_normal_(self.linear1.weight)
nn.init.zeros_(self.linear1.bias)

# 对第二个隐藏层的权重使用 Kaiming 初始化，偏置初始化为0
# nonlinearity='relu' 参数指明这种初始化是为ReLU激活函数设计的
nn.init.kaiming_normal_(self.linear2.weight, nonlinearity='relu')
nn.init.zeros_(self.linear2.bias)

# 2. 定义前向传播路径，即“拼接积木”
# 当我们调用 model(data) 时，PyTorch会自动执行此方法
def forward(self, x):
# 数据流经第一个隐藏层，并应用 Sigmoid 激活函数
x = self.linear1(x)
x = torch.sigmoid(x)

# 数据流经第二个隐藏层，并应用 ReLU 激活函数
x = self.linear2(x)
x = torch.relu(x)

# 数据流经输出层
x = self.out(x)
# 应用 Softmax 激活函数，得到每个类别的概率
# dim=-1 表示在最后一个维度（这里是特征维度）上进行 Softmax
x = torch.softmax(x, dim=–1)

return x

2. 运行模型并观察结果

接下来，我们编写一个函数来实例化模型，并用随机数据进行一次前向传播，看看数据的形状是如何变化的。

# 创建一个函数来运行和测试模型
def run_demo():
# 实例化模型对象
my_model = Model()

# — 准备输入数据 —
# 随机生成一个 5×3 的张量，模拟一个批次(batch_size=5)的数据，每个数据有3个特征
my_data = torch.randn(5, 3)
print("输入数据 (my_data):\\n", my_data)
print("输入数据形状 (my_data.shape):", my_data.shape)

# — 将数据送入模型进行前向传播 —
output = my_model(my_data)
print("\\n输出数据 (output):\\n", output)
print("输出数据形状 (output.shape):", output.shape)

# — 使用 torchsummary 计算并打印模型参数信息 —
print("\\n====== 使用 torchsummary 分析模型 ======")
# input_size=(3,) 表示单个样本的特征数是3
summary(my_model, input_size=(3,), batch_size=5)

# — 手动遍历并查看模型的可学习参数 (权重w和偏置b) —
print("\\n====== 查看模型具体参数 ======")
for name, parameter in my_model.named_parameters():
print(f"参数名: {name}")
print(parameter.data)
print("-" * 30)

if __name__ == '__main__':
run_demo()

三、结果分析与参数计算详解

运行上述代码，我们可以得到详细的输出结果，我们来逐一分析。

1. 观察数据形状变化

• 输入：[5, 3] 表示我们有5个样本，每个样本有3个特征。
• 输出：[5, 2] 表示经过网络处理后，我们得到了5个样本的预测结果，每个结果是一个包含2个值的向量，这两个值代表了该样本属于两个类别的概率。
• 这个过程清晰地展示了数据在网络中如何从输入维度 in_features=3 转换到输出维度 out_features=2。

mydata.shape–––> torch.Size([5, 3])
output.shape–––> torch.Size([5, 2])
mydata–––>
tensor([[–0.3714, –0.8578, –1.6988],
[ 0.3149, 0.0142, –1.0432],
[ 0.5374, –0.1479, –2.0006],
[ 0.4327, –0.3214, 1.0928],
[ 2.2156, –1.1640, 1.0289]])
output–––>
tensor([[0.5095, 0.4905],
[0.5218, 0.4782],
[0.5419, 0.4581],
[0.5163, 0.4837],
[0.6030, 0.3970]], grad_fn=<SoftmaxBackward>)

2. 模型参数计算（核心重点！）

torchsummary 库为我们提供了一个非常直观的模型结构和参数统计表：

—————————————————————-
Layer (type) Output Shape Param #
================================================================
Linear-1 [5, 3] 12
Linear-2 [5, 2] 8
Linear-3 [5, 2] 6
================================================================
Total params: 26

这里的 Param # 是如何计算的呢？我们来手动拆解一下，这一点对于初学者理解网络结构至关重要！

核心公式：参数量 = 输入维度 × 输出维度 + 输出维度 (即 w 的数量 + b 的数量)

• 第一个隐藏层 (Linear-1)

  • 输入维度 in_features = 3
  • 输出维度 out_features = 3
  • 权重 w 的数量 = 3 * 3 = 9
  • 偏置 b 的数量 = 3 (每个输出神经元一个偏置)
  • 总参数量 = 9 + 3 = 12

• 第二个隐藏层 (Linear-2)

  • 输入维度 in_features = 3 (来自上一层的输出)
  • 输出维度 out_features = 2
  • 权重 w 的数量 = 3 * 2 = 6
  • 偏置 b 的数量 = 2
  • 总参数量 = 6 + 2 = 8

• 输出层 (Linear-3)

  • 输入维度 in_features = 2 (来自上一层的输出)
  • 输出维度 out_features = 2
  • 权重 w 的数量 = 2 * 2 = 4
  • 偏置 b 的数量 = 2
  • 总参数量 = 4 + 2 = 6

总计：12 + 8 + 6 = 26 个可训练参数，与工具分析的结果完全一致！

图解第一个隐藏层的参数计算：

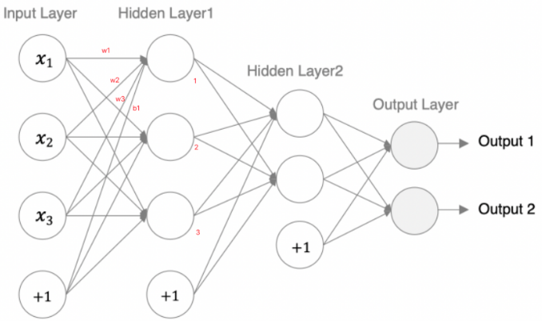
重要提示：一定要分清输入数据和网络权重是两回事！数据是流动的，而权重是网络自身的、需要通过训练学习的固定参数。

四、神经网络的优缺点

最后，我们简单总结一下神经网络这种方法的普遍优缺点：

优点 👍

缺点 👎

📜 总结

恭喜你！通过这篇文章，你不仅理解了如何使用 PyTorch 从零搭建一个自定义的神经网络的思路，还掌握了如何分析其结构、计算参数量。

核心要点回顾：

• 继承 nn.Module，在 __init__ 中定义层，在 forward 中定义数据流。
• 使用合理的参数初始化方法是成功训练的关键。
• 参数量的计算公式 in * out + out 是理解网络复杂度的基础。

希望这篇文章能成为你深度学习之路上的一个坚实台阶。如果你觉得有帮助，别忘了点赞、收藏、关注三连哦！我们下期再见！