《征服相位差：基于FFT标定与数字补偿的高精度计量实现》

引言：从问题到解决方案的跨越

在上一篇的探索中，我们揭示了理想功率模型的脆弱性：面对一个简单的台式风扇（感性负载），基于 P = Uᵣₘₛ × Iᵣₘₛ 的计算结果竟显著偏离真实值。我们认识到，其根源在于电压与电流波形之间存在的相位差（φ）。

然而，更深入的剖析带来了更严峻的挑战：我们通过ADC采样直接获得的"相位差"，并非负载特性的纯净反映，而是一个由负载真实相移（φ_load） 与测量系统固有误差（φ_system） 叠加而成的混合信号：

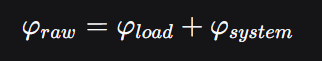
若不能将二者精确分离，任何精密测量都无从谈起。这引出了两个核心问题：

本章将系统性地解答这些问题。我们将以快速傅里叶变换（FFT） 为核心工具，构建一套从"标定"到"补偿"的完整数字处理链路，实现从嘈杂的现实数据中提取出真实的电气参数，完成高精度计量的最终跨越。

一、相位差的精确捕获：FFT频谱分析法

要在数字域捕获相位差，需将时间上的波形偏移转化为可计算的相位角度。FFT方法因其精度和频域洞察力成为首选。

1.1 核心原理：从时域到频域的映射

FFT将时域信号分解为一系列复数频率分量。对于经同步采样获得的电压序列 u[n] 和电流序列 Iraw[n]，分别进行FFT后，可得到各自的复数表示：

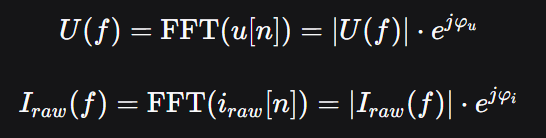
则原始相位差可直接计算为：

1.2 关键实现步骤

二、系统固有误差的标定：寻找"零位"基准

分离 φ_system 的关键在于建立一个已知 φ_load = 0 的参考状态，此时测量出的 φ_raw 即为 φ_system。

2.1 标定流程

三、数字补偿的核心：频域旋转法

获得系统延时 τ 后，补偿的目标是：在数字域抵消这个固定延时的影响。直接在时域对采样序列进行移位和插值不仅计算复杂，且会引入新的误差。一种在数学上严格等价、在工程上更优雅的方法是频域旋转补偿法。

3.1 理论基础：时延的频域等价操作

信号处理中的时移定理指出：时域上的一个固定延时 τ，完全等价于在频域乘以一个复数旋转因子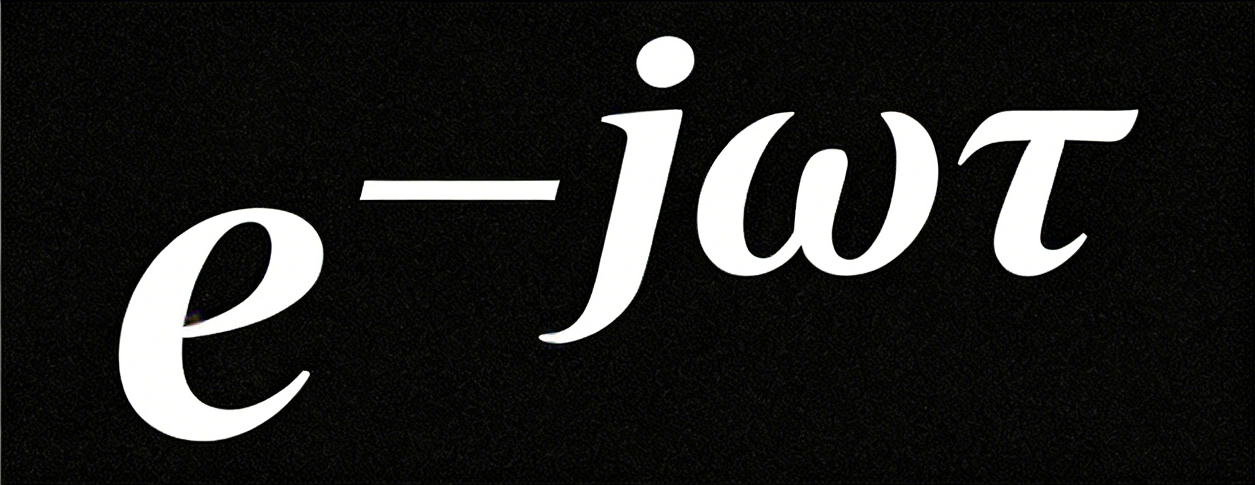（其中 ω = 2πf）。

对于我们的系统，ADC采样到的电流信号 isampled(t)可表示为真实电流 i(t)的延时版本：

其频谱关系为：

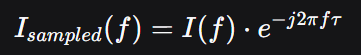
这个旋转因子只改变复频谱的相位角，而不改变其幅度。它在每个频率点 f 上，都将真实电流的相位向后旋转了 2πfτ 弧度。

3.2 补偿操作：在FFT域内逆转旋转

既然系统误差是在频域上做了"减法旋转"，那么补偿就是对其做"加法旋转"。我们通过复数乘法，对电流频谱进行补偿：

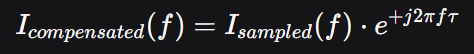
补偿后的频谱 Icompensated(f)，其相位已与真实电流 I(f) 的相位完全相同。

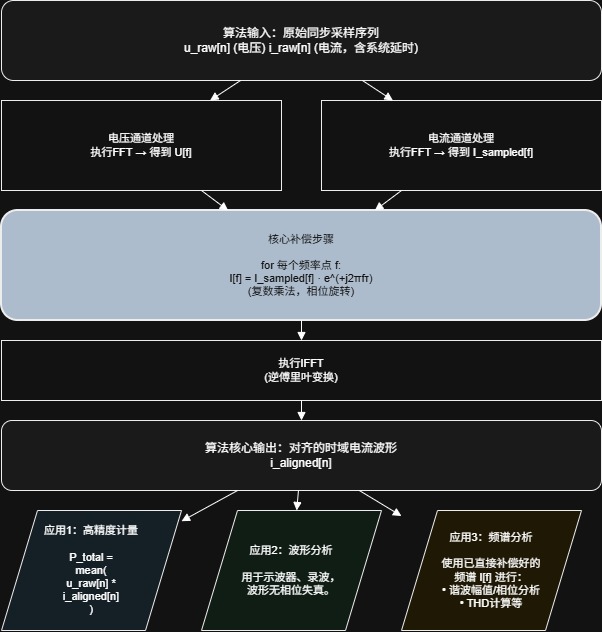
3.3 完整算法流程：从补偿到波形重建

该方法的强大之处在于，它不仅能修正相位用于计算，更能重建出在时域上与电压严格对齐的电流波形，为所有后续分析提供纯净数据源。其完整的数据处理链如下：

3.4 STM32实现关键代码（基于CMSIS-DSP库）

/**
* 功率分析器核心数据结构
* 注：为简洁起见，省略部分辅助成员
*/
typedef struct {
// 核心配置
uint32_t fft_size; // FFT点数（2的幂）
float32_t sampling_freq; // 采样频率

// 数据缓冲区
float32_t *voltage_data; // 电压采样
float32_t *current_data; // 电流原始采样
float32_t *current_aligned; // 补偿后电流

// 系统参数
float32_t system_delay; // 标定得到的系统延时
bool is_calibrated; // 标定状态
bool is_compensated; // 补偿状态

// FFT处理实例
arm_rfft_fast_instance_f32 fft_instance;
} PowerAnalyzer;

/**
* 频域旋转补偿法
* 原理：通过复数乘法在频域消除系统延时影响
* 数学基础：时域延时 τ ↔ 频域旋转因子 e^{-j2πfτ}
*/
bool PowerAnalyzer_Compensate(PowerAnalyzer *analyzer, float32_t *temp_buffer)
{
// 参数检查
if (!analyzer || !analyzer->is_calibrated) return false;

// Step 1: 时域 → 频域（电流信号）
arm_rfft_fast_f32(&analyzer->fft_instance, current_data, fft_buffer, 0);

// Step 2: 频域相位旋转补偿（核心操作）
if (fabsf(analyzer->system_delay) > 1e-9f) {
// 实数FFT特殊格式处理
// fft_buffer[0]: DC分量
// fft_buffer[1]: 奈奎斯特频率
// fft_buffer[2k], fft_buffer[2k+1]: 频率k的复数表示

// 处理直流分量（不需要补偿）
// fft_buffer[0] 保持不变

// 处理奈奎斯特频率
if (analyzer->fft_size >= 2) {
float32_t nyquist_freq = analyzer->sampling_freq / 2.0f;
float32_t phase = 2 * PI * nyquist_freq * analyzer->system_delay;
fft_buffer[1] *= cosf(phase); // 只有实部
}

// 处理其他频率分量
for (uint32_t k = 1; k < analyzer->fft_size/2; k++) {
float32_t freq = k * analyzer->sampling_freq / analyzer->fft_size;
float32_t phase = 2 * PI * freq * analyzer->system_delay;

// 生成旋转因子
float32_t cos_factor = cosf(phase);
float32_t sin_factor = sinf(phase);

// 复数乘法：I_comp = I_raw * e^{j2πfτ}
uint32_t idx_re = 2 * k;
uint32_t idx_im = idx_re + 1;

float32_t re = fft_buffer[idx_re];
float32_t im = fft_buffer[idx_im];

fft_buffer[idx_re] = re * cos_factor – im * sin_factor;
fft_buffer[idx_im] = re * sin_factor + im * cos_factor;
}
}

// Step 3: 频域 → 时域（获取补偿后波形）
arm_rfft_fast_f32(&analyzer->fft_instance, fft_buffer, current_aligned, 1);

analyzer->is_compensated = true;
return true;
}

四、全波有功功率的终极计算：时域积分法

通过上述补偿，我们获得了与电压波形在时域上严格对齐的电流序列ialigned[n]。基于此，计算全波有功功率最权威、最直接的方法是回归其物理定义——瞬时功率的平均值。

4.1 计算公式

全波有功功率 Ptotal的定义是瞬时功率在一个周期内的平均值。对于离散系统：

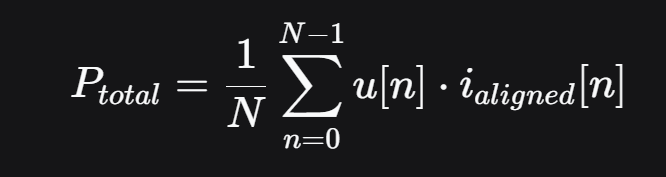
其中：

• N 为一个完整周期内的采样点数

• u[n] 为电压采样序列

• ialigned[n]为补偿对齐后的电流采样序列

4.2 完整功率计算实现

4.3 完整的功率计算框架

/**
* 有功功率计算：时域积分法
* 公式：P = (1/N) * Σ(u[n] * i[n])
* 特点：物理意义明确，精度最高
*/
void PowerAnalyzer_CalculatePower(PowerAnalyzer *analyzer)
{
float32_t sum_ui = 0, sum_u2 = 0, sum_i2 = 0;

// 选择电流数据源：补偿后或原始
float32_t *current = analyzer->is_compensated ?
analyzer->current_aligned :
analyzer->current_data;

// 时域积分计算
for (uint32_t i = 0; i < analyzer->fft_size; i++) {
float32_t u = analyzer->voltage_data[i];
float32_t i_val = current[i];

sum_ui += u * i_val; // 瞬时功率累加
sum_u2 += u * u; // 电压平方累加
sum_i2 += i_val * i_val; // 电流平方累加
}

// 计算各参数
uint32_t N = analyzer->fft_size;
analyzer->power_active = sum_ui / N;
analyzer->voltage_rms = sqrtf(sum_u2 / N);
analyzer->current_rms = sqrtf(sum_i2 / N);
analyzer->power_apparent = analyzer->voltage_rms * analyzer->current_rms;

// 功率因数计算（含保护机制）
if (analyzer->power_apparent > 1e-6f) {
analyzer->power_factor = analyzer->power_active / analyzer->power_apparent;
// 限制在[-1, 1]范围内
analyzer->power_factor = fmaxf(-1.0f, fminf(1.0f, analyzer->power_factor));
}
}

五、总结与展望

至此，我们完成了高精度交流计量系统的闭环构建：