机器学习——PCA数据降维

主成分分析（PCA）

什么是主成分分析

PCA，全称主成分分析，本质上是一种数据压缩技术。是一种通用的降维工具

它的核心目标的是在减少数据维度的同时，尽可能保留原始数据的关键信息。

举个直观的例子：我们要分析一批花朵数据，原始数据包含萼片长、萼片宽、花瓣长、花瓣宽四个特征。通过PCA处理后，可能只需要两个主成分就能解释原始数据90%以上的信息。这意味着我们可以抛弃原来的四个维度，只用两个维度进行后续分析，不仅计算量大大减少，还能避免不同特征间的相互干扰。

这里需要明确一个关键认知：PCA不是简单地删除某些特征，而是通过重新构建特征的方式实现降维。它不会丢失重要信息，而是将分散在多个维度上的信息集中到少数几个主成分中，让数据变得更易处理。

什么是降维

数据的特征又叫做数据的维度，减少数据的特征即降维

如何做到最好的降维效果？

减少数据维度的同时，能较好地代表原始数据。

如何进行主成分分析

虽然 PCA 背后涉及向量、协方差、特征值等数学概念，但我们完全可以跳过复杂公式，用通俗的逻辑理解其工作流程：

第一步：数据预处理 （数据标准化）

PCA 对数据的尺度很敏感，比如一个特征的单位是 “千米”，另一个特征的单位是 “米”，数值差异会导致分析结果偏向数值大的特征。因此，在进行 PCA 之前，需要先对数据进行标准化处理（比如零均值化），让每个特征的均值为 0，避免因量纲不同带来的偏差。

第二步：寻找 “主成分”—— 抓住数据的核心方向

PCA 的核心是找到几个 “最优方向”，这些方向就是主成分。

判断 “最优” 的标准很简单：数据在这个方向上的分布最分散。因为数据越分散，说明这个方向上包含的信息越多。

第三步：数据转换 —— 完成降维操作

找到 k 个主成分后，就可以将原始高维数据映射到这 k 个主成分构成的新空间中，这个过程就是降维。最终得到的 k 维数据，就是 PCA 处理后的结果，它保留了原始数据的大部分信息，却有着更简洁的结构。

举个实际应用场景：某电商平台收集了用户的 10 个行为特征（浏览时长、点击次数、加购数等），通过 PCA 提取出 2 个主成分，第一个主成分可理解为 “用户活跃度”，第二个主成分可理解为 “消费意愿”。原本 10 维的用户数据，变成了 2 维的 “活跃度 – 消费意愿” 数据，后续无论是用户分群还是精准营销，都变得简单高效。

为什么进行主成分分析

在实际应用中，高维数据带来的问题远比我们想象的复杂，而 PCA 恰好能精准解决这些痛点：

1. 告别 “维度灾难”，提升计算效率

高维数据会让计算量呈指数级增长。比如在机器学习中，特征维度越多，模型训练时间越长，硬件开销也越大。如果原本有 100 个特征，通过 PCA 降到 10 个主成分，计算量会大幅降低，模型训练速度可能提升数倍，同时还能避免因维度过多导致的过拟合问题。

2. 消除多重共线性，优化分析结果

很多实际数据中，不同特征之间往往存在相关性。比如 “身高” 和 “体重” 两个特征，通常呈正相关关系 —— 这种多重共线性会干扰回归分析、聚类等模型的结果，导致参数估计不准确。PCA 通过构建相互独立的主成分，能彻底消除特征间的冗余关联，让分析结果更可靠。

3. 简化数据可视化，便于直观理解

人类的认知能力有限，很难直接理解三维以上的数据。而 PCA 可以将高维数据降到二维或三维，让我们能够通过散点图、折线图等方式直观展示数据分布。比如将用户行为的十几个特征通过 PCA 降到二维，就能清晰看到不同用户群体的聚类情况，为决策提供直观依据。

4.噪声过滤

PCA 还能在一定程度上过滤噪声数据。原始数据中难免存在测量误差等噪声，这些噪声通常分布在方差较小的维度上，而 PCA 聚焦于方差较大的主成分，相当于自动忽略了噪声带来的干扰，让数据更 “干净”。

PCA中的数学

基变换

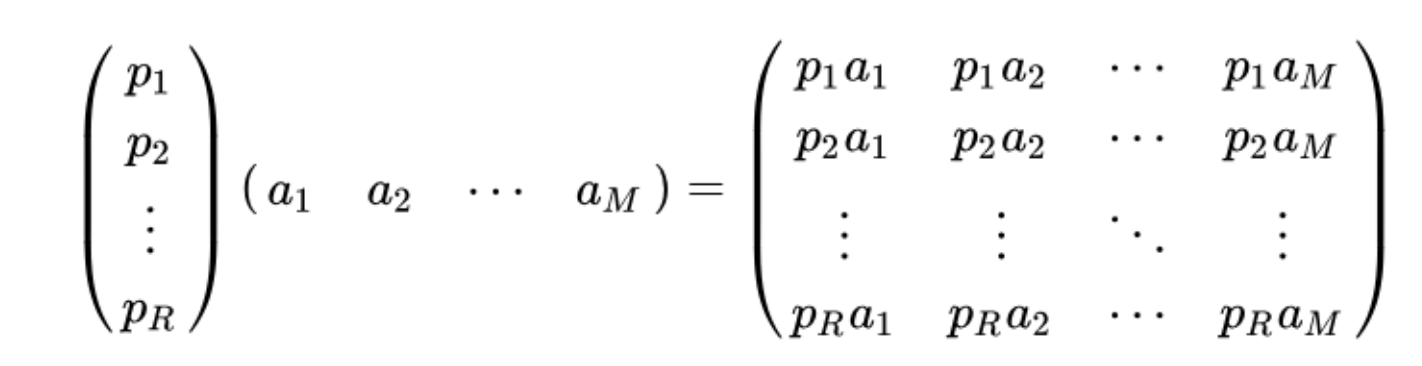
pi为行向量,表示第i个基；

aj为列向量,表示第j个数据

基变换的含义

1.两个矩阵相乘的意义是将右边矩阵中的每一列列向量变换到左边矩阵中，每一行行向量为基所表示的空间中去。

2.抽象地说，一个矩阵可以表示一种线性变换。

PCA执行步骤总结

1. 将原始数据按列组成n行m列矩阵X；

2.将X的每一行（代表一个属性字段）进行零均值化， 即减去这一行的均值

3.求出协方差矩阵：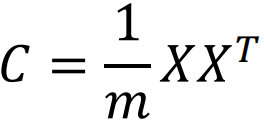

4.求出协方差矩阵的特征值及对应的特征向量；

5.将特征向量按对应特征值大小从上到下按行排列 成矩阵，取前k行组成矩阵P;

6.Y=PX即为降维到k维后的数据

PCA优劣势分析

优点

1.计算方法简单，容易实现。

2.可以减少指标筛选的工作量。

3.消除变量间的多重共线性。

4.在一定程度上能减少噪声数据。

缺点

1.特征必须是连续型变量。

2.无法解释降维后的数据是什么。

3.贡献率小的成分有可能更重要。

PCA 的代码实现示例（Python）

使用 scikit-learn 实现 PCA 的完整流程：

import numpy as np
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt

# 1. 加载数据（以鸢尾花数据集为例）
data = load_iris()
X = data.data # 4维特征
y = data.target

# 2. 数据预处理
scaler = StandardScaler() # 标准化（可选，根据数据决定）
X_scaled = scaler.fit_transform(X)

# 3. 执行PCA
pca = PCA() # 先保留所有主成分，查看方差贡献率
X_pca = pca.fit_transform(X_scaled)

# 4. 选择最佳k值（绘制累计方差贡献率）
explained_variance = pca.explained_variance_ratio_
cumulative_variance = np.cumsum(explained_variance)

plt.plot(range(1, len(cumulative_variance)+1), cumulative_variance, 'o-')
plt.xlabel('主成分数量')
plt.ylabel('累计方差贡献率')
plt.axhline(y=0.95, color='r', linestyle='–') # 95%阈值线
plt.show()

# 5. 用选定的k值重新降维（例如k=2）
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)

# 6. 可视化降维结果
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y, cmap='viridis')
plt.xlabel('主成分1')
plt.ylabel('主成分2')
plt.title('PCA降维后的数据分布')
plt.show()
# 总结

PCA 的核心是通过线性变换将高维数据映射到低维空间，其数学本质是对协方差矩阵的特征分解（或数据矩阵的 SVD 分解）。实际应用中需注意：
– 必须进行均值中心化，标准化视场景选择
– 主成分数量 \\( k \\) 需通过累计方差贡献率等方法合理选择
– 对异常值敏感，需预处理
– 线性结构适用，非线性数据可考虑核 PCA

深入理解 PCA 不仅能更好地应用于数据降维，还能帮助理解其他降维方法（如 t-SNE、LDA）的设计思路，为复杂数据分析任务提供基础工具。