字节常考算法题记录(自用)

自用记录

注意这里都是写在acm模式下的要考虑输入输出，还有这种默认是面试的时候给样例本地跑，而不是直接跑测题机。所以可能有的像输入是null的/极端情况没考虑，那种到时候跑一次发现不对了直接加上就行。

有的写法是直接思路实现的，可能复杂度对但不够优雅（写起来很麻烦）之后看到更好的会改的w

1.最长不含重复字符的子字符串

第一遍有个顺序写反了排了会debug也有15min？

第二遍记得细节3分钟出来

package t1;

import java.util.HashSet;
import java.util.Scanner;

public class main {
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
String s=sc.next();
int sl=s.length(),l=0,r=0,jg=0;
HashSet<Character>hash=new HashSet<>();
while(r<sl){
if(hash.contains(s.charAt(r))){
jg=Math.max(jg,r–l);
while(l<=r){
hash.remove(s.charAt(l));
l++;
if(s.charAt(l–1)==s.charAt(r))break;
}
}
hash.add(s.charAt(r));
r++;
}
jg=Math.max(jg,r–l);
System.out.println(jg);
}
}

时间复杂度O（N)

2. 二叉树的锯齿形层序遍历

第一遍30min以上，对这种细节下起来不知道为什么这么慢，但也是寿司出来了，就是bfs+栈不知道为什么写得这么慢

还有acm模式树的输入也要记得（感觉正常的话会直接预制树）

第二遍知道思路一直在敲也敲了11min

package t2;

import java.util.*;

class TreeNode {
int val;
TreeNode left;
TreeNode right;

TreeNode() {
}

TreeNode(int val) {
this.val = val;
}

TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}

public class main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
Integer a[] = new Integer[15];
int sl = sc.nextInt(), f1 = 1;
for (int i = 1; i <= sl; i++) {
String s = sc.next();
if (s.equals("null")) a[i] = null;
else a[i] = Integer.parseInt(s);
}
Deque<TreeNode> b = new ArrayDeque<>();
TreeNode root = new TreeNode(a[1]);
b.addLast(root);
while (!b.isEmpty()) {
if (f1 * 2 + 1 > sl) break;
TreeNode c = b.pollFirst(), d = new TreeNode(a[f1 * 2] == null ? –1 : a[f1 * 2]), e = new TreeNode(a[f1 * 2 + 1] == null ? –1 : a[f1 * 2 + 1]);
c.left = d;
c.right = e;
f1++;
b.addLast(d);
b.addLast(e);
}

int cs = 1, f = 0;
Deque<TreeNode> d = new ArrayDeque<>();
d.addLast(root);
List<List<Integer>> jg1 = new ArrayList<>();
while (!d.isEmpty()) {
int bl = cs;
cs *= 2;
f++;
List<Integer> jg2 = new ArrayList<>();
Deque<Integer> jg3 = new ArrayDeque<>();
for (int i = 0; i < bl; i++) {
if (!d.isEmpty()) {
TreeNode t1 = d.pollFirst(), t1l = t1.left, t1r = t1.right;
jg3.addLast(t1.val);
if (t1l==null||t1l.val == –1) {
cs—;
} else {
d.addLast(t1l);
}
if (t1r==null||t1r.val == –1) {
cs—;
} else {
d.addLast(t1r);
}
}
}
if (f % 2 == 1) {
while (!jg3.isEmpty()) {
jg2.add(jg3.pollFirst());
}
} else {
while (!jg3.isEmpty()) {
jg2.add(jg3.pollLast());
}
}
jg1.add(jg2);
}
for (List<Integer> jg11 : jg1) {
for (Integer i : jg11) {
System.out.print(i + " ");
}
System.out.println();
}
}

}

时间复杂度O（N）就是bfs的时间复杂度

3. 数组中的第K个最大元素

记得这个是妙妙题，想不起来的话就想不起来了

投降看下题解

时间nlogn的排序谁都知道，时间n的堆但是也要n的空间也知道，主要忘了时间n空间1看题解是快排类似的快速选择

package t3;

import java.util.Scanner;

public class main {
static int a[] = new int[1005];

static int quicksort1(int l, int r, int bm) {
if (l >= r) return a[l];
int zj = quicksort2(l, r);
if (zj == bm) {
return a[zj];
} else if (zj < bm) {
return quicksort1(zj + 1, r, bm);
} else {
return quicksort1(l, zj – 1, bm);
}
}

static int quicksort2(int l, int r) {
int bj = a[l];
while (l < r) {
if (a[r] < bj) {
a[l] = a[r];
l++;
while (l < r) {
if (a[l] > bj) {
a[r] = a[l];
r—;
break;
} else l++;
}
} else r—;
}
a[l] = bj;
return l;
}

public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int sl = sc.nextInt(), wz = sl – sc.nextInt() + 1;
for (int i = 0; i < sl; i++) {
a[i + 1] = sc.nextInt();
}
System.out.println(quicksort1(1, sl, wz));
}
}

就是快排改了下只找bm在的区域，时间复杂度分析：

贴个ai的图

这里为了方便就直接选最左边为基准了，随机选能防止卡常，他要问也可以说

4. 反转链表

写了7min很神秘，我敲得太慢了吗（？）

package t4;

import java.util.Scanner;

class Node{
int val;
Node next;
Node(){}
Node(int x){val=x;}
}
public class main {
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
int n=sc.nextInt();
Node root=new Node(–11111),bl1=root;
for (int i = 0; i < n; i++) {
int x=sc.nextInt();
bl1.next=new Node(x);
bl1=bl1.next;
}
Node bl2=root.next,pre=root;
while (bl2 != null) {
Node temp= bl2.next;
bl2.next=pre;
pre=bl2;
bl2=temp;
}
while (bl1!=null&&bl1.val!=–11111){
System.out.println(bl1.val);
bl1=bl1.next;
}
}
}

双指针时间O（N）空间O（1）比递归空间O（N）好点

5. LRU 缓存机制

不知道这个题到时候会不会给力扣那样的已知条件

大概9min

package t5;

import java.util.LinkedHashMap;

public class main {
int sl;
LinkedHashMap<Integer, Integer> map = new LinkedHashMap<>();

main(int sl) {
this.sl = sl;
}

int get(int k) {
if (map.containsKey(k)) {
int v = map.get(k);
map.remove(k);
map.put(k, v);
return v;
} else return –1;
}

void put(int k, int v) {
if (map.containsKey(k)) {
map.remove(k);
map.put(k, v);
} else {
if (map.size() == sl) {
map.remove(map.keySet().iterator().next());
map.put(k, v);
} else map.put(k, v);
}
}

}

主要是别忘了用迭代器map.remove(map.keySet().iterator().next());来移除第一个最老的

6.三数之和

非常经典！

第一遍搓了14min还是慢（）

package t6;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.Scanner;

public class main {
static int a[]=new int[10005];
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
List<List<Integer>> jg1 = new ArrayList<>();
for (int i = 0; i < n; i++) {
a[i] = sc.nextInt();
}
if (n < 3) System.out.println(jg1);
else {
Arrays.sort(a, 0, n);
for (int i = 0; i < n; i++) {
if (i != 0 && a[i] == a[i – 1]) continue;
if (a[i] > 0) break;
int l = i + 1, r = n – 1;
while (l < r) {
while (l < r && a[l] + a[r] != –a[i]) {
if (a[l] + a[r] > –a[i]) {
r—;
} else if (a[l] + a[r] < –a[i]) {
l++;
}
}
if (l!=r&&a[l] + a[r] + a[i] == 0) {
List<Integer> jg2 = new ArrayList<>();
jg2.add(a[i]);
jg2.add(a[l]);
jg2.add(a[r]);
jg1.add(jg2);
}
while (l + 1 < n && a[l + 1] == a[l]) l++;
while (r – 1 > 0 && a[r – 1] == a[r]) r—;
l++;
r—;
}
}
System.out.println(jg1);
}
}
}

直接分析复杂度：

最暴力的是O（N^{3)就是三重遍历，优化一下想到两数之和的hashmap用在这里是O（NlogN），再想一下发现无论怎样复杂度都很大，会大于排序的nlogn所以直接排序用双指针达到O（N}2)

7. 买卖股票的最佳时机

写了一下4min原来是纸老虎，我看字节老问还以为很难，就是一维dp时间O（N）

package t7;

import java.util.Scanner;

public class main {
static int a[] = new int[10005], b[] = new int[10005];

public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt(), jg = 0;
for (int i = 0; i < n; i++) {
a[i] = sc.nextInt();
}
for (int i = n – 1; n >= 0; i—) {
if (i == n – 1) b[i] = a[i];
else
b[i] = Math.max(b[i + 1], a[i]);
}
for (int i = 0; i < n; i++) {
jg = Math.max(jg, b[i] – a[i]);
}
System.out.println(jg);
}
}

8. 二叉树的最近公共祖先

这道题我应该做过但是想不到最优思路

这道题我想不到什么好的思路，我的第一想法是dfs找两个节点的高度，然后根据两个节点的路径看相同高度时候是不是同一个节点第一个这个数就是答案。我感觉想麻烦了但是应该能做复杂度也符合要求。

看题解：从上往下找，都找到了能确定父节点。再因为递归特性，能确定从下到上第一个找到的就是答案。

知道了思路实现也花了大概20min，递归太不熟了

package t8;

import java.util.ArrayDeque;
import java.util.Deque;
import java.util.Scanner;

class TreeNode {
int val;
TreeNode left;
TreeNode right;

TreeNode() {
}

TreeNode(int val) {
this.val = val;
}
}

public class main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
Integer a[] = new Integer[150];
int sl = sc.nextInt(), f1 = 1;
for (int i = 1; i <= sl; i++) {
String s = sc.next();
if (s.equals("null")) a[i] = null;
else a[i] = Integer.parseInt(s);
}
Deque<TreeNode> b = new ArrayDeque<>();
TreeNode root = new TreeNode(a[1]);
b.addLast(root);
while (!b.isEmpty()) {
if (f1 * 2 + 1 > sl) break;
TreeNode c = b.pollFirst(), d = new TreeNode(a[f1 * 2] == null ? –1 : a[f1 * 2]), e = new TreeNode(a[f1 * 2 + 1] == null ? –1 : a[f1 * 2 + 1]);
c.left = d;
c.right = e;
f1++;
b.addLast(d);
b.addLast(e);
}
//上面都是输入树，下面那点是答案
int x = sc.nextInt(), y = sc.nextInt();
System.out.println(lowestCommonAncestor(root, x, y).val);
}

static TreeNode lowestCommonAncestor(TreeNode root, int p, int q) {
if (root==null||root.val == p || root.val == q) return root;
TreeNode left = lowestCommonAncestor(root.left, p, q);
TreeNode right = lowestCommonAncestor(root.right, p, q);
if(left!=null&&right!=null)return root;
return left==null ?right:left;
}
}

复杂度on

9. 相交链表

想了会思路带实现大概10min

这个思路有点不记得了，就记得和公共有关系，要换边走。也有点忘了怎么判断没有交点。(发现不用判断，没交点也会最后==只不过都是null，正常返回就好)

（这种需要结论证明的常考题目，就直接记结论吧，唉唉）

ListNode getIntersectionNode(ListNode a, ListNode b) {
ListNode c = a, d = b;
while (c!=d) {
while (c != null && d != null && c != d) {
c = c.next;
d = d.next;
}
if (c == d) {
break;
}
if (c == null) c = b;
else d = a;

}
return c;
}

这个的acm感觉太不友好的输入了，就用核心代码了

复杂度on

10. 搜索旋转排序数组

这个有点费脑袋，可以背（？）

while(l<r){int m=l+(r–l)/2; if(a[m]>a[r]) l=m+1; else r=m;}

需要知道这个能找到旋转次数，这个是在找最小的数好知道位移次数，这里是左大右小，所以大了右移。

int r = (mid2 + l1) % n;

通过这个来映射完成二分

package t10;

import java.util.Scanner;

public class main {
static int a[] = new int[10005];

public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt(), x = sc.nextInt();
for (int i = 0; i < n; i++) {
a[i] = sc.nextInt();
}

int l1 = 0, r1 = n – 1, mid1 = 0;
while (l1 < r1) {
mid1 = (l1 + r1) / 2;
if (a[mid1] <= a[r1]) l1 = mid1 – 1;
else r1 = mid1;
}

int l2 = 0, r2 = n – 1, mid2 = 0, f = 0;
while (l2 <= r2) {
mid2 = (l2 + r2) / 2;
int r = (mid2 + l1) % n;
if (a[r] == x) {
System.out.println(r);
f = 1;
break;
} else if (a[r] > x) {
r2 = mid2 – 1;
} else {
l2 = mid2 + 1;
}
}
if (f == 0)
System.out.println(–1);
}
}

复杂度logn

11. 接雨水

这里我有两个思路：

横着接雨水：每个左找到第一个大于等于他的右然后算一下，算是模拟写起来麻烦还要处理边界。也可以配合单调栈使用可能好写点，不过时间复杂度没变都是ON，还多了ON空间。

竖着接雨水：双指针复杂度也是ON，写起来也好写，就是针对每一个看他左右的最大，一维dp再压缩空间O1。

package t11;

import java.util.Scanner;

public class main {
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
int n=sc.nextInt(),a[]=new int[n+1],jg=0,m1=0,m2=0,l=0,r=n–1;
for (int i = 0; i < n; i++) {
a[i]=sc.nextInt();
}
while(l<=r){
m1=Math.max(m1,a[l]);
m2=Math.max(m2,a[r]);
if(m1<=m2){
jg+=Math.max(0,m1–a[l]);
l++;
}
else{
jg+=Math.max(0,m2–a[r]);
r—;
}
}

System.out.println(jg);
}
}

时间ON空间O1(想到是每个元素的左右最大，再dp压过来的就知道怎么写了)

12. 螺旋矩阵

模拟唉唉讨厌赤石，不过唤醒以前的记忆想起来s,x,z,r就能写起来很舒服

package t12;

import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;

public class main {
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
int a[][]=new int[1005][1005];
int n=sc.nextInt(),m=sc.nextInt();
for (int i = 0; i < n; i++) {
for (int i1 = 0; i1 < m; i1++) {
a[i][i1]=sc.nextInt();
}
}
List<Integer>jg=new ArrayList<>();
int s=0,x=n–1,z=0,r=m–1;
while(true){
for(int i=z;i<=r;i++)jg.add(a[s][i]);
if(++s>x)break;
System.out.println(jg);
for(int i=s;i<=x;i++)jg.add(a[i][r]);
if(—r<z)break;
System.out.println(jg);
for(int i=r;i>=z;i—)jg.add(a[x][i]);
if(—x<s)break;
System.out.println(jg);
for(int i=x;i>=s;i—)jg.add(a[i][z]);
if(++z>r)break;
System.out.println(jg);
}
System.out.println(jg);
}
}

建议写的时候也把输出写上，不管到时候要不要找bug也可以看得更清楚（）

时间on^2空间o1不过模拟谈复杂度感觉没什么必要

13. 合并两个有序链表

想明白思路再写（不然容易变成猪咪，先看能不能思路过样例）

package t13;

import java.util.Scanner;

class ListNode {
int val;
ListNode next;

ListNode(int x) {
val = x;
next = null;
}
}

public class main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt(), m = sc.nextInt();
ListNode r1 = new ListNode(–1), r2 = new ListNode(–2), bl1 = r1, bl2 = r2, wei = new ListNode(–3), jg = wei;
for (int i = 0; i < n; i++) {
int x = sc.nextInt();
bl1.next = new ListNode(x);
bl1 = bl1.next;
}
for (int i = 0; i < m; i++) {
int x = sc.nextInt();
bl2.next = new ListNode(x);
bl2 = bl2.next;
}

bl1 = r1.next;
bl2 = r2.next;
while (bl1 != null && bl2 != null) {
if (bl1.val <= bl2.val) {
wei.next = bl1;
bl1 = bl1.next;
} else {
wei.next = bl2;
bl2 = bl2.next;
}
wei=wei.next;
}
wei.next = bl1 == null ? bl2 : bl1;
jg=jg.next;
while (jg != null) {
System.out.print(jg.val+" ");
jg = jg.next;
}

}
}

注意下细节和思路，复杂度ON

14. 合并K个升序链表

第一思路是合并两个升序链表带入但是复杂度是O(N * K)

优化后好想的是优先队列时间O(N * logK)但是空间O（N) 分治时间O（N * K）且空间O(1)就是k-1次改成两两合并

类似归并排序

package t14;

import java.util.Scanner;

class ListNode {
int val;
ListNode next;

ListNode(int x) {
val = x;
next = null;
}
}

public class main {
static ListNode a[] = new ListNode[1005];

public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();

for (int i = 0; i < n; i++) {
int m = sc.nextInt();
ListNode wei = new ListNode(–1), jg = wei;
for (int i1 = 0; i1 < m; i1++) {
int x=sc.nextInt();
wei.next = new ListNode(x);
wei = wei.next;
}
a[i] = jg.next;
}
ListNode merge = merge(0, n – 1);
while (merge!=null){
System.out.print(merge.val+" ");
merge=merge.next;
}
}

static ListNode merge(int l, int r) {
if (l == r) {
return a[l];
}
int mid = (l + r) / 2;
ListNode l1 = merge(l, mid);
ListNode r1 = merge(mid + 1, r);
return mergeTwoLists(l1, r1);
}

static ListNode mergeTwoLists(ListNode r1, ListNode r2) {
ListNode bl1 = r1, bl2 = r2, wei = new ListNode(–3), jg = wei;
while (bl1 != null && bl2 != null) {
if (bl1.val <= bl2.val) {
wei.next = bl1;
bl1 = bl1.next;
} else {
wei.next = bl2;
bl2 = bl2.next;
}
wei = wei.next;
}
wei.next = bl1 == null ? bl2 : bl1;
return jg.next;
}
}

主要就是归并配和合并两个（归并和快排的写法都是重要的）

15. 从前序与中序遍历序列构造二叉树

我投降，我大概是没写过这种。草2025.8.10提交过，哈哈

看题解吧，还是不擅长递归，太fw了

package t15;

import java.util.HashMap;
import java.util.Map;
import java.util.Scanner;

class TreeNode {
int val;
TreeNode left;
TreeNode right;

TreeNode() {
}

TreeNode(int val) {
this.val = val;
}

TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}

public class main {
static int a[] = new int[1005], b[] = new int[1005];
static Map<Integer, Integer> map = new HashMap<>();

//l1 r1 l2 r2是数组对应的做或者有的气势
static TreeNode build(int l1, int r1, int l2, int r2) {
if (l1 > r1) return null;
int rv = a[l1];
TreeNode root = new TreeNode(rv);
int wz = map.get(rv);
int zb = wz – l2;
root.left = build(l1 + 1, l1 + zb, l2, wz – 1);
root.right = build(l1 + zb + 1, r1, wz + 1, r2);
return root;
}

public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt(), m = sc.nextInt();
for (int i = 0; i < n; i++) {
a[i] = sc.nextInt();
}
for (int i = 0; i < m; i++) {
b[i] = sc.nextInt();
}
for (int i = 0; i < m; i++) {
map.put(b[i], i);
}
TreeNode build = build(0, n – 1, 0, m – 1);
dfs(build);
}

static void dfs(TreeNode a) {
if (a == null) return;
System.out.println(a.val);
dfs(a.left);
dfs((a.right));
}
}

时间复杂度分析O(N)如果没用hashmap会是O(N^2)，感觉难想的点还是

root.left = build(l1 + 1, l1 + zb, l2, wz – 1);
root.right = build(l1 + zb + 1, r1, wz + 1, r2);

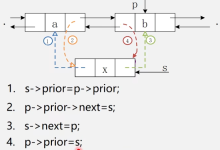
16. 重排链表

这道题第一眼有了大概思路，但感觉麻烦，看了题解是一样的，草。还是老老实实实现去吧。

package t16;

import java.util.Scanner;

class ListNode {
int val;
ListNode next;

ListNode(int x) {
val = x;
next = null;
}
}
public class main {
static ListNode zb;
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
int n=sc.nextInt();
ListNode wei=new ListNode(–2),bl1=wei,k=wei,m=wei;
for (int i = 0; i < n; i++) {
bl1.next=new ListNode(sc.nextInt());
bl1=bl1.next;
}
zb=wei.next;
while (k!=null&&k.next!=null){
k=k.next.next;
m=m.next;
}
ListNode b=m.next;
m.next=null;//断开连接是有必要的
digui(b);
wei=wei.next;
while (wei!=null){
System.out.print(wei.val+" ");
wei=wei.next;
}
}
static void digui(ListNode a){
if(a==null)return;
digui(a.next);
ListNode temp=zb.next;
zb.next=a;
a.next=temp;
zb=temp;
}
}

(孩子们0:07了，我会赢吗，能在睡前写完25吗)

复杂度O（N)

17.数值的整数次方

快速幂吗，有点忘了说是，主要Java的biginteger类的modpow的实现就是快速幂。。。还要手撕

package t17;

import java.util.Scanner;

public class main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
double a = sc.nextDouble(), jg = 1, sum = –1;
int b = sc.nextInt(), sl = 0;
if (b < 0) b *= –1;
a = 1 / a;
sum = a;
String er = Integer.toBinaryString(b);
sl = er.length();
for (int i = sl – 1; i >= 0; i—) {
if (er.charAt(i) == '1') {
jg *= sum;
}
sum *= sum;
}
System.out.println(jg);
}
}

时间复杂度分析logn，直接暴力的话要ON，但是我这种还有logn的空间，如果不想要就用下面那种

顺便看一下以前的快速幂板子

while (b != 0) {
if (b % 2)
jg =(jg* a)%p;
a = (a*a)%p;
b /= 2;
}

只能说老了，怕记不住，上面的通俗易懂点（？）

18. 全排列

送分题！小小dfs斩于马下

package t18;

import java.util.Scanner;

public class main {
static int a[] = new int[1005], f[] = new int[1005], b[] = new int[1005], n;

public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
for (int i = 0; i < n; i++) {
a[i] = sc.nextInt();
}
dfs(0);
}

static void dfs(int x) {
if (x == n) {
for (int i = 0; i < n; i++) {
System.out.printf("%d ", a[b[i]]);
}
System.out.println();
}
for (int i = 0; i < n; i++) {
if (f[i] == 0) {
f[i] = 1;
b[x] = i;
dfs(x + 1);
f[i] = 0;
}
}
}
}

复杂度时间n * n!空间n。会了这个就等于会了八皇后（）

19. 岛屿数量

package t19;

import java.util.Scanner;

public class main {
static char a[][] = new char[1005][1005];
static int ydh[] = {–1, 0, 1, 0}, ydl[] = {0, 1, 0, –1}, n, m, jg;

public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
jg = 0;
for (int i = 0; i < n; i++) {
a[i] = sc.next().toCharArray();
}

for (int i = 0; i < n; i++) {
for (int i1 = 0; i1 < m; i1++) {
if (a[i][i1] == '1') {
jg++;
dfs(i, i1);
}
}
}
System.out.println(jg);
}

static void dfs(int h, int l) {
if(a[h][l]=='0')return;
a[h][l]='0';
for (int i = 0; i < 4; i++) {
int h1 = ydh[i] + h, l1 = ydl[i] + l;
if (h1 > –1 && h1 < n&&l1>–1&&l1<m){
dfs(h1,l1);
}
}
}
}

感觉这种递归比起树和链表还是太仁慈了

时间O（N^2)空间O(N2)

20. 反转链表 II

package t20;

import java.util.Scanner;

class ListNode {
int val;
ListNode next;

ListNode(int x) {
val = x;
next = null;
}
}
public class main {
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
int n=sc.nextInt(),z=sc.nextInt(),r=sc.nextInt(),f=0;
ListNode wei=new ListNode(–1),bl1=wei,bl2=wei,bl3=null,bl4=null,bl5=null,bl6=null,bl7=null;
for (int i = 0; i < n; i++) {
int x=sc.nextInt();
bl1.next=new ListNode(x);
bl1=bl1.next;
}
bl1=wei;
for (int i = 0; i < z –1; i++) {
bl1=bl1.next;
}bl3=bl1.next;bl5=bl1;
for (int i = 0; i < r; i++) {
bl2=bl2.next;
}bl4=bl2.next;
while(bl3!=bl4){
if(f==0){
f=1;
bl7=bl3;
}
if(bl3.next==bl4)bl6=bl3;
ListNode temp=bl3.next;
bl3.next=bl1;
bl1=bl3;
bl3=temp;
}bl5.next=bl6;bl7.next=bl3;
wei=wei.next;
while(wei!=null){
System.out.println(wei.val);
wei=wei.next;
}
}
}

别看7个bl写的很神秘，但是改为核心后力扣一遍过很爽好吧

复杂度O（N)把

21.最长递增子序列

好像是刻进dna的dp题目,二分贪心最优解nlogn，暴力dp O(N^2)

package t21;

import java.util.Arrays;
import java.util.Scanner;

public class main {
static int a[] = new int[1005], b[] = new int[1005], n;

public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
for (int i = 0; i < n; i++) {
a[i] = sc.nextInt();
}
Arrays.fill(b, 10005);
int jg = 0;
for (int i = 0; i < n; i++) {
int wz = Arrays.binarySearch(b, a[i]);
if (wz < 0) {
wz = –wz – 1;
if (b[wz] == 10005) jg++;
b[wz] = a[i];
}
}
System.out.println(jg);
}
}

二分贪心尾数数组很妙，可以多想想别忘了

复杂度nlogn

22. K 个一组翻转链表

/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public static ListNode reverseKGroup(ListNode head, int k) {
ListNode j = new ListNode(0), jg = null, x = j;
int f = 0;
j.next = head;
while (true) {
int pd = 0;
x = j;
while (j != null && pd < k) {
j = j.next;
pd++;
}
if (j == null) break;
ListNode a = x, b = x.next, sum3 = j.next,qd=null;
while (b != sum3) {
if (b == j) {
if (f == 0) {
jg = b;
f = 1;
}
qd=b;
}
ListNode temp = b.next;
b.next = a;
a = b;
b = temp;
}
j = x.next;
j.next = sum3;
x.next=qd;
}
return jg;
}

}

这道题目比较吃逻辑，可以多想想

23. 最小栈

import java.util.ArrayDeque;
import java.util.Date;
import java.util.Deque;

//leetcode submit region begin(Prohibit modification and deletion)
class MinStack {
Deque<Integer> stack1;
Deque<Integer> stack2;

public MinStack() {
stack1 = new ArrayDeque<>();
stack2 = new ArrayDeque<>();
}

public void push(int val) {
stack1.addLast(val);
if(stack2.isEmpty()||val<=stack2.getLast())stack2.addLast(val);
}

public void pop() {
Integer i = stack1.pollLast();
if(i.equals(stack2.getLast()))stack2.pollLast();
}

public int top() {
return stack1.getLast();
}

public int getMin() {
return stack2.getLast();
}
}

注意下思路就行，常数获取min空间换时间，还有要注意push那里条件<=没有等于min栈可能会空

24. 两数之和

package t24;

import java.util.HashMap;
import java.util.Scanner;

public class main {
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
int n=sc.nextInt(),x=sc.nextInt(),a[]=new int[10005];
HashMap<Integer,Integer> map=new HashMap<>();
for (int i = 0; i < n; i++) {
a[i]=sc.nextInt();
}

for (int i = 0; i < n; i++) {
if(map.containsKey(a[i])){
int jg[]={map.get(a[i]),i};
for (int i1 : jg) {
System.out.println(i1);
}break;
}
map.put(x–a[i],i);
}
}
}

送分题，nlogn

25. 合并区间

package t25;

import java.util.Arrays;
import java.util.Scanner;

public class main {
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
int n=sc.nextInt(),a[][]=new int[105][2],b[][]=new int[105][2],f=0;
for (int[] ints : a) {
Arrays.fill(ints,10005);
}
for (int i = 0; i < n; i++) {
for (int i1 = 0; i1 < 2; i1++) {
a[i][i1]=sc.nextInt();
}
}

Arrays.sort(a,(o,p)->{
if(o[0]==p[0]) return o[1]–p[1];
else return o[0]–p[0];
});

for (int i = 0; i < n; i++) {
if(i==n–1){
b[f][0]=a[i][0];b[f++][1]=a[i][1];break;
}
int r=i+1;
if(a[i][1]>=a[r][0]){
while(r<n&&a[i][1]>=a[r][0]){
r++;
}
if(r==n)a[i][1]=Math.max(a[i][1],a[r–1][1]);
else
a[i][1]=a[r–1][1];
}b[f][0]=a[i][0];b[f++][1]=a[i][1];i=r–1;

}
for (int i = 0; i < f; i++) {
System.out.printf("%d %d\\n",b[i][0],b[i][1]);
}
}
}

排序真是太方便了，拯救了这个。注意下二维数组的排序方法要重写一个东西。剩下就是合并细节排序后只需要考虑两个了。时间复杂度是nlogn排序了

其他

我觉得有意思的题目

560. 和为 K 的子数组