逻辑回归的对数损失

什么是对数？一句话讲透

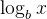$\\log_b x$ 的意思就是：要把 b 乘自己多少次，才能得到 x。

更正式一点：

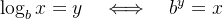
$\\log_b x = y \\quad \\Longleftrightarrow \\quad b^y = x$

也就是说：对数是在“反问指数”。

指数：给你 y，算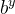得到 x
对数：给你 x，反过来问“指数 y 是多少”

你可以把“对数”当成一种常用的“压缩尺度”

现实里很多量跨度巨大（比如声音分贝、地震震级、数据大小），用对数可以把“乘法增长”变成“加法增长”，更好看、更好比较。

这张图讲的就是逻辑回归（Logistic Regression）最核心的损失函数：对数损失（Log Loss / Logarithmic Loss），也叫交叉熵损失（Cross Entropy Loss）。我用很通俗的方式把它讲透。

1）逻辑回归到底在输出什么？

逻辑回归不是直接输出“0 或 1”，而是输出一个概率：

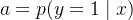
$a = p(y=1\\mid x)$

a 越接近 1：模型越确信样本是 1
a 越接近 0：模型越确信样本是 0

这个 a 通常来自 sigmoid：

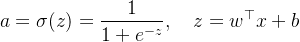
$a=\\sigma(z)=\\frac{1}{1+e^{-z}},\\quad z=w^\\top x+b$

2）对数损失长什么样？（图里那两条曲线）

图上有两条曲线：

✅ 当真实标签 y=1 时（蓝线）

你希望模型给出 a 越大越好（越接近 1 越对）

损失定义为：

$L=-\\log(a)$

如果 a=1：−log⁡(1)=0，完美，损失 0
如果 a=0.1：−log⁡(0.1)≈2.30，错得很离谱，损失大
如果 a→0：−log⁡(a)→+∞，“自信地错”会被极度惩罚

这就是蓝线左高右低的原因。

✅ 当真实标签 y=0 时（红线）

你希望模型给出 a 越小越好（越接近 0 越对）

此时损失定义为：

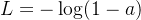
$L=-\\log(1-a)$

因为 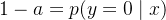$1-a = p(y=0\\mid x)$

如果 a=0：−log⁡(1)=0，完美
如果 a=0.9：−log⁡(0.1)≈2.30，错得很离谱
如果 a→1：−log⁡(1−a)→+∞，自信错同样严重

这就是红线右高左低的原因。

3）把两种情况合起来，就是一个统一公式

你看到图上那个分段形式：

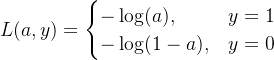
$\\begin{array}{c} L(a,y)= \\begin{cases} -\\log(a), & y=1\\\\ -\\log(1-a), & y=0 \\end{cases} \\end{array}$

可以合并成一个更常用的形式：

$\\boxed{ L(a,y)= -\\left[y\\log(a)+(1-y)\\log(1-a)\\right] }$

这就是逻辑回归的对数损失 / 交叉熵损失。

4）为什么要用 “log”？直觉非常重要！

你可以把它理解成一句话：

模型越“自信地答错”，就罚得越狠。

举个特别直观的例子

真实是 y=1：

预测概率 a损失 −log⁡(a) 感觉

0.9	0.105	“基本答对”
0.6	0.511	“有点犹豫”
0.1	2.303	“非常自信但错了”

你会发现：

从 0.9 → 0.6，损失增加一点点（还能接受）
从 0.6 → 0.1，损失暴涨（错得太离谱）

这就是 log 的“惩罚加速”效果。

5）它其实等价于“最大似然”的推导结果

如果你把模型输出看成概率：

当 y=1，模型给出概率 a
当 y=0，模型给出概率 1−a

那么一个样本的“模型认为它发生的概率”可以写成：

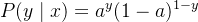
$P(y\\mid x)=a^y(1-a)^{1-y}$

训练时，我们希望“这些真实标签出现的概率尽量大”
→ 最大化概率（似然）
→ 等价于最小化负对数似然

$-\\log P(y\\mid x) = -\\left[y\\log(a)+(1-y)\\log(1-a)\\right]$

所以对数损失不是拍脑袋定的，它是非常自然、合理的统计结果。

6）一句话总结图的含义（你看懂就赢了）

蓝线 −log⁡(a)：真实是 1 时，a 越小越惨
红线 −log⁡(1−a)：真实是 0 时，a 越大越惨
在 0.5 附近两条线交叉：表示“你不确定”时损失都差不多

我们继续，用一个超具体、能手算的小例子，把逻辑回归的 log loss 从头算到尾（还顺便看懂“mini-batch 平均损失”）。

1）先定一个 mini-batch：3 个样本

我们假设模型已经算出了每个样本“是正类 y=1”的概率 a。

样本	真实标签 y	模型预测概率 a=p(y=1∣x)
1	1	0.9
2	1	0.6
3	0	0.2

2）按公式逐个算 log loss

统一公式：

$L(a,y)= -\\left[y\\log(a)+(1-y)\\log(1-a)\\right]$

默认 log 是自然对数 ln⁡。

✅ 样本1：y=1, a=0.9

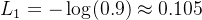
$L_1 = -\\log(0.9) \\approx 0.105$

解释：模型预测 90% 是正类，而且真的是正类 → 损失很小

✅ 样本2：y=1, a=0.6

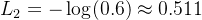
$L_2 = -\\log(0.6) \\approx 0.511$

解释：模型也猜对了，但没那么自信 → 损失比样本1大

✅ 样本3：y=0, a=0.2

注意：真实是 0，就要用 −log⁡(1−a)

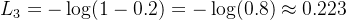
$L_3 = -\\log(1-0.2) = -\\log(0.8) \\approx 0.223$

解释：模型给正类概率 0.2，意思是“我觉得你 80% 是负类”
而真实确实是负类 → 损失也小

3）mini-batch 的总损失 = 平均损失

逻辑回归训练时最常用的 batch loss：

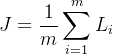
$J = \\frac{1}{m}\\sum_{i=1}^{m}L_i$

这里 m=3

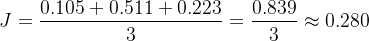
$J=\\frac{0.105+0.511+0.223}{3} =\\frac{0.839}{3} \\approx 0.280$

✅ 这就是这一个 mini-batch 的交叉熵损失。

4）感受一下“自信错了会被罚爆”的威力

我们把样本3改成一个“很离谱的预测”：

真实仍然 y=0，但模型却给 a=0.99（极度相信它是正类）

那么：

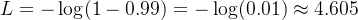
$L=-\\log(1-0.99) = -\\log(0.01)\\approx 4.605$

你看：

正确且合理：a=0.2 → 损失 0.223
自信地错：a=0.99 → 损失 4.605（直接爆炸）

📌 这就是 log loss 的灵魂：

你可以不确定，但你不能“自信地错”。

5）你图里的两条曲线，现在就完全通了

当 y=1：损失 −log⁡(a)
- a→1：损失 →0
- a→0：损失 →+∞
当 y=0：损失 −log⁡(1−a)
- a→0：损失 →0
- a→1：损失 →+∞

所以你看到的就是：

蓝线（y=1）左边高、右边低
红线（y=0）左边低、右边高

6）再送你一个“超级记忆口诀”

你只要记住一句话就够了：

✅ 真实是什么，就看模型给它的概率有多大；概率越小，惩罚越大，而且是 log 级爆炸。

真实是 1 → 看 a
真实是 0 → 看 1−a

我们下一步继续讲更关键的一点：
为什么逻辑回归训练时，经常会出现一个特别漂亮的结果：

$\\frac{\\partial L}{\\partial z} = a - y$

也就是“误差 = 预测 – 真实”，梯度形式极其简洁（反向传播里非常爽）。

我们继续把最关键、最“爽”的一步讲透：

为什么逻辑回归 + 对数损失的梯度，会变成超级简洁的：
$\\displaystyle \\frac{\\partial L}{\\partial z}=a-y$

这一步一旦懂了，你就能真正明白：
逻辑回归为什么这么好训练、为什么梯度下降这么顺。

0）先把变量关系画出来（链式法则通道）

逻辑回归是：

$z = w^\\top x + b$

$a = \\sigma(z)=\\frac{1}{1+e^{-z}}$

$L(a,y)= -\\left[y\\log(a)+(1-y)\\log(1-a)\\right]$

所以计算梯度时就是一条链：

$z \\rightarrow a \\rightarrow L$

我们想要的是：

$\\frac{\\partial L}{\\partial z} = \\frac{\\partial L}{\\partial a}\\cdot\\frac{\\partial a}{\\partial z}$

1）先求 $\\frac{\\partial L}{\\partial a}$

$L= -\\left[y\\log(a)+(1-y)\\log(1-a)\\right]$

对 a 求导：

$\\frac{d}{da}\\log(a)=\\frac{1}{a}$
$\\frac{d}{da}\\log(1-a)=\\frac{-1}{1-a}$

所以：

$\\frac{\\partial L}{\\partial a} = -\\left(y\\cdot \\frac{1}{a}+(1-y)\\cdot\\frac{-1}{1-a}\\right)$

整理一下：

$\\frac{\\partial L}{\\partial a} = -\\frac{y}{a}+\\frac{1-y}{1-a}$

2）再求 $\\frac{\\partial a}{\\partial z}$ （sigmoid 的导数）

a=σ(z)

一个非常经典的结论：

$\\frac{\\partial a}{\\partial z}=a(1-a)$

3）链式法则相乘： $\\frac{\\partial L}{\\partial z}$

$\\frac{\\partial L}{\\partial z} = \\left(-\\frac{y}{a}+\\frac{1-y}{1-a}\\right)\\cdot a(1-a)$

把 a(1−a) 分别乘进去：

$\\frac{\\partial L}{\\partial z} = -\\frac{y}{a}\\cdot a(1-a)+\\frac{1-y}{1-a}\\cdot a(1-a)$

约掉：

$= -y(1-a) + (1-y)a$

展开：

$= -y + ya + a - ya$

中间 ya 抵消了，剩下：

$\\boxed{\\frac{\\partial L}{\\partial z}=a-y}$

✅ 这就是神奇的简洁结果！

4）这个结果为什么“特别有直觉”？

$\\frac{\\partial L}{\\partial z}=a-y$

它说的就是一句话：

梯度 = 预测概率 − 真实标签

如果真实 y=1，但你预测 a=0.2
$\\Rightarrow a-y = 0.2-1=-0.8$ （负数很大）
👉 说明你应该把 z 往上推（让 a 变大）
如果真实 y=0，但你预测 a=0.9
$\\Rightarrow a-y = 0.9-0=0.9$ （正数很大）
👉 说明你应该把 z 往下压（让 a 变小）

所以它特别像你熟悉的“误差”：

$\\text{error} = \\text{prediction} - \\text{target}$

5）再进一步：求到 w 和 b 的梯度（训练要用）

因为：

$z=w^\\top x+b$

所以：

$\\frac{\\partial z}{\\partial w}=x,\\quad \\frac{\\partial z}{\\partial b}=1$

链式法则：

$\\frac{\\partial L}{\\partial w} = \\frac{\\partial L}{\\partial z}\\cdot\\frac{\\partial z}{\\partial w} = (a-y)x$

$\\frac{\\partial L}{\\partial b} = \\frac{\\partial L}{\\partial z}\\cdot\\frac{\\partial z}{\\partial b} = (a-y)$

✅ 最终训练更新公式就是：

$w \\leftarrow w-\\eta (a-y)x$

$b \\leftarrow b-\\eta (a-y)$

6）用一个小数值演示一次更新（直观到爆）

假设某个样本：

x=[2, 1]
y=1
当前模型预测 a=0.3（明显偏低）

那么：

$a-y=0.3-1=-0.7$

所以：

$\\frac{\\partial L}{\\partial w}=(a-y)x=-0.7[2,1]=[-1.4,-0.7]$

梯度下降更新 $w := w-\\eta \\nabla w$ ：

$w \\leftarrow w-\\eta[-1.4,-0.7] = w + \\eta[1.4,0.7]$

你看到了吗？因为你预测太小，所以更新会让 w 变大，从而让 z 变大、a 变大 —— 预测更接近 1。

✅ 方向完全符合直觉。

7）一句话总结这一段的“核心爽点”

逻辑回归 + 对数损失最漂亮的地方就是：

$\\boxed{\\frac{\\partial L}{\\partial z}=a-y}$

这让反向传播变得极其简单、稳定、好优化。

什么是对数？一句话讲透

你可以把“对数”当成一种常用的“压缩尺度”

1）逻辑回归到底在输出什么？

2）对数损失长什么样？（图里那两条曲线）

✅ 当真实标签 y=1 时（蓝线）

✅ 当真实标签 y=0 时（红线）

3）把两种情况合起来，就是一个统一公式

4）为什么要用 “log”？直觉非常重要！

举个特别直观的例子

5）它其实等价于“最大似然”的推导结果

6）一句话总结图的含义（你看懂就赢了）

1）先定一个 mini-batch：3 个样本

2）按公式逐个算 log loss

✅ 样本1：y=1, a=0.9

✅ 样本2：y=1, a=0.6

✅ 样本3：y=0, a=0.2

3）mini-batch 的总损失 = 平均损失

4）感受一下“自信错了会被罚爆”的威力

5）你图里的两条曲线，现在就完全通了

6）再送你一个“超级记忆口诀”

0）先把变量关系画出来（链式法则通道）

1）先求 $\\frac{\\partial L}{\\partial a}$

2）再求 $\\frac{\\partial a}{\\partial z}$ （sigmoid 的导数）

a=σ(z)

3）链式法则相乘： $\\frac{\\partial L}{\\partial z}$

4）这个结果为什么“特别有直觉”？

5）再进一步：求到 w 和 b 的梯度（训练要用）

6）用一个小数值演示一次更新（直观到爆）

7）一句话总结这一段的“核心爽点”

相关推荐

评论抢沙发

评论前必须登录！

热门标签

置顶推荐

热门文章

最新文章

什么是对数？一句话讲透

你可以把“对数”当成一种常用的“压缩尺度”

1）逻辑回归到底在输出什么？

2）对数损失长什么样？（图里那两条曲线）

✅ 当真实标签 y=1 时（蓝线）

✅ 当真实标签 y=0 时（红线）

3）把两种情况合起来，就是一个统一公式

4）为什么要用 “log”？直觉非常重要！

举个特别直观的例子

5）它其实等价于“最大似然”的推导结果

6）一句话总结图的含义（你看懂就赢了）

1）先定一个 mini-batch：3 个样本

2）按公式逐个算 log loss

✅ 样本1：y=1, a=0.9

✅ 样本2：y=1, a=0.6

✅ 样本3：y=0, a=0.2

3）mini-batch 的总损失 = 平均损失

4）感受一下“自信错了会被罚爆”的威力

5）你图里的两条曲线，现在就完全通了

6）再送你一个“超级记忆口诀”

0）先把变量关系画出来（链式法则通道）

1）先求

2）再求 ​（sigmoid 的导数）

a=σ(z)

3）链式法则相乘：

4）这个结果为什么“特别有直觉”？

5）再进一步：求到 w 和 b 的梯度（训练要用）

6）用一个小数值演示一次更新（直观到爆）

7）一句话总结这一段的“核心爽点”

相关推荐

评论 抢沙发

评论前必须登录！

热门标签

置顶推荐

热门文章

最新文章

1）先求 $\\frac{\\partial L}{\\partial a}$

2）再求 $\\frac{\\partial a}{\\partial z}$ （sigmoid 的导数）

3）链式法则相乘： $\\frac{\\partial L}{\\partial z}$

评论抢沙发