云计算百科
云计算领域专业知识百科平台
当前位置：网硕互联帮助中心 > 服务器百科 > 正文

最小生成树：Kruskal算法(C语言)

2026-01-13 分类：服务器百科 阅读(5) 评论(0)

文章目录

  • kruskal算法
    • 理论
      • 生成树的定义
      • 生成树的属性
      • 应用场景
      • 最小生成树（MiniTree）
      • 克鲁斯卡尔（Kruskal）算法
      • 边集数组
    • 代码
      • 头文件
        • 邻接矩阵
        • Kruskal
      • 实现函数
        • 邻接矩阵
        • Kruskal
      • 测试函数
  • 所有代码
    • 邻接矩阵
    • Kruskal

kruskal算法

理论

生成树的定义

⼀个连通图的生成树是⼀个极小的连通子图，它包含图中全部的n个顶点，但只有构成⼀棵树的n-1条边==。对于一棵树，顶点数 n 和边数 m 满足关系 m=n−1==

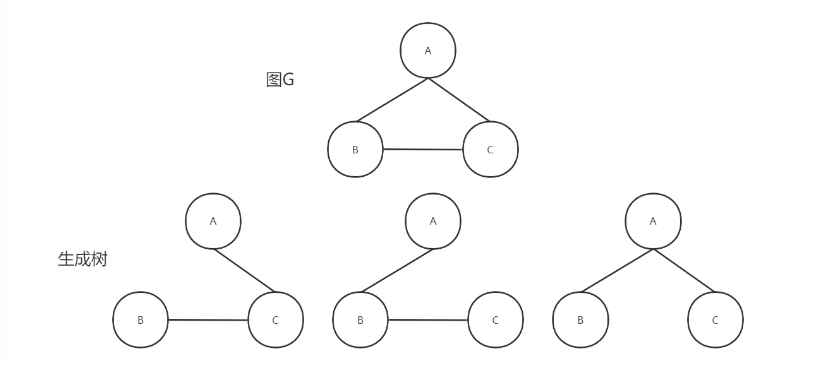
在这里插入图片描述

生成树的属性

  • 一个连通图可以多个生成树
  • 一个连通图的所有生成树都包含相同的顶点数和边数
  • 树里面没有环，生成树也没有
  • 移除生成树的任意一条边都会导致图的不连通，生成树的最小边特性
  • 在生成树中添加一条边会构成环
  • 对于包含n个顶点的连通图，生成树包含n个顶点和n-1条边
  • 包含n个顶点的无向完全图最多包含C n（上标） 2（下标）

应用场景

计算机网络，路由器内核有用到最小生成树

最小生成树（MiniTree）

所谓⼀个带权图的最最小成树，就是原图中边的权值最小的生成树 ，所谓最小是指边的权值之和小于或者等于其它生成树的边的权值之和。

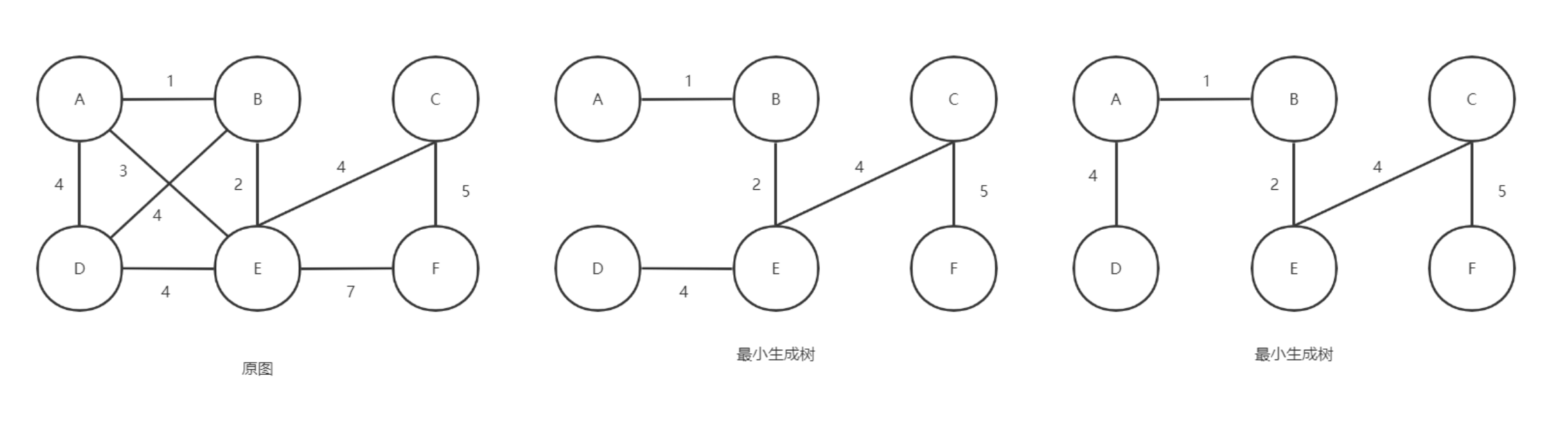
在这里插入图片描述

克鲁斯卡尔（Kruskal）算法

m条边，n个顶点，m条边里面找n-1条边，他们的和是最小的，而且他们会构成最小生成树（无向图）

约束

  • 加了一条边，不会产生环

通过并查集查找，在不在一个集合，在就不用加这条边了，多余了

边集数组

边集数组，或称边数组，是一种用来表示图的数据结构。它的核心思想非常简单： 用一个一维数组来存储图中的所有边，数组中的每个元素对应一条边。

代码

头文件

邻接矩阵

#pragma once
#pragma once
#define MAXNODENUM 20
//节点结构
typedef struct {
int no;
const char* show;//指针指向名字数组
}MatrixVexNode;

//边结构
typedef int MatrixVexEdge;

//图结构
typedef struct {

MatrixVexNode ver[MAXNODENUM];//顶点数组
MatrixVexEdge edge[MAXNODENUM][MAXNODENUM];//矩阵
//权重填在邻接矩阵里面
int nodeNum;
int edgeNum;
int directed;
}MGraph;

//初始化图//多少个节点
void initMGraph(MGraph* g, const char* nodename[], int edgeVaule, int directed, int num);
//添加边//索引
void addMGraphEdge(MGraph* g, int x, int y,int w);

//遍布
int MNodevisited[MAXNODENUM];//全局变量开始已经全0
void DFSMGraphTravel(MGraph* g, int v);
void initalizevisited();
void BFSMGraphTravel(MGraph* g, int v);

Kruskal

#pragma once
//根据邻接矩阵来生成边集数组
#include"MGraph.h"
typedef struct {
int vervex1;
int vervex2;
int weight;
}EdgeSet;

//创建 传进来边的数量
EdgeSet* createEdgeSet(int n);

//初始化
int initEdgeSet(EdgeSet* edge, MGraph* g, int num);

//排序
void sqrtEdgeSet(EdgeSet* edge, int edgeNum);

//Kruskal
//返回最小生成树的权值
int Kruskal(EdgeSet* edge, EdgeSet* result, MGraph* g, int edgeNum);

实现函数

邻接矩阵

#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include"MGraph.h"

//初始化图//开始初始化为一个值表示没边//多少个节点
void initMGraph(MGraph* g, const char* nodename[], int edgeVaule, int directed, int num) {
if (g == NULL || nodename == NULL) {
return;
}
memset(g, 0, sizeof(MGraph));
g->directed = directed;
g->edgeNum = 0;
g->nodeNum = num;

for (int i = 0; i < num; i++)
{
g->ver[i].no = i;
g->ver[i].show = nodename[i];

for (int j = 0; j < num; j++)
{
g->edge[i][j] = edgeVaule;
}
}

}
static int IsEdge(int w) {
if (w > 0 && w < INF) {
return 1;
}
return 0;
}
//一条条添加边//索引
void addMGraphEdge(MGraph* g, int x, int y, int w) {
if (g == NULL) {
return;
}

if (x < 0 || x >= g->nodeNum || y < 0 || y >= g->nodeNum) {
return;
}
//边而且权值合法而且没加过边过的情况下
if (IsEdge(w))
{
g->edge[x][y] = w;
g->edgeNum++;

//如果无方向
if (g->directed == 0) {
g->edge[y][x] = w;
}

}

}

Kruskal

创建边集数组

//创建 传进来边的数量 n为邻接矩阵已经记录的边数量
EdgeSet* createEdgeSet(int n) {
EdgeSet* edge = malloc(n*sizeof(EdgeSet));
if (edge == NULL)return NULL;
memset(edge, 0, sizeof(EdgeSet));

return edge;
}

初始化（默认无向图）

返回实际边的数量

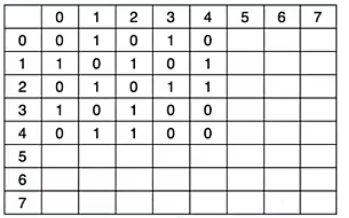
在这里插入图片描述

从邻接矩阵（MGraph）中提取所有边，并存储到边集数组（EdgeSet *edges）中

就是把边集数组全部填满

/初始化
//通过传进来的邻接矩阵来 初始化 边集数组
//通过邻接矩阵的边的权值二维数组 约束条件 权值大于0
//num 为顶点的数量
//返回+1=边数量 (边集数组的索引+1)
int initEdgeSet(EdgeSet* edge, MGraph* g, int num) {
if (g == NULL|| edge ==NULL)return –1;

int k = 0;//记录的边个数
for (int i = 0; i < num; i++)
{
for (int j = i+1; j < num; j++)//i 0 j 1 i 1 j 2 i3j4
{
if (g->edge[i][j] > 0) {
edge[k].vervex1 = i;
edge[k].vervex2 = j;
edge[k].weight = g->edge[i][j];
k++;
}
}
}

return k;
}

j = i + 1 这个循环条件的目的是避免重复记录无向图的同一条边。

假设有4个顶点的图：

text

邻接矩阵： 0 1 2 3 0 [0, 2, 3, 0] 1 [2, 0, 4, 5] 2 [3, 4, 0, 6] 3 [0, 5, 6, 0]

遍历过程（只遍历上三角）：

  • i=0: j=1,2,3 → 记录坐标(0,1)、(0,2)的边 （0,3）为0
  • i=1: j=2,3 → 记录坐标(1,2)、(1,3)的边
  • i=2: j=3 → 记录坐标(2,3)的边
  • i=3: 无（j从4开始，已超出范围）

排序

利用临时变量进行 排序

//排序 选择排序
//memcpy函数
void sqrtEdgeSet(EdgeSet* edge,int edgeNum) {
if (edge == NULL)return ;
EdgeSettemp;

for (int i = 0; i < edgeNum; i++)
{
for (int j = i+1; j < edgeNum; j++)
{
if (edge[j].weight < edge[i].weight) {
memcpy(&temp, &edge[j], sizeof(EdgeSet));
memcpy(&edge[j], &edge[i], sizeof(EdgeSet));
memcpy(&edge[i], &temp, sizeof(EdgeSet));
}
}

}
}

内存拷贝 memcpy

void *p：表示可以接收任意空间地址

不关心怎么访问，退化为字节访问

Kruskal

  • 先建立并查集并初始化
  • 在已经排序的边集数组里面遍历所有的边 满足条件的放进去 结果 边集数组
  • 约束条件是权值>0边存在以及这两个顶点不是一个集合里面的
  • 满足条件就加一已选择的边数 结束条件就是顶点数-1（树有n个顶点就有n-1个边）

    • static int findRoot( int* Uset,int v) {
    if (Uset == NULL)return –1;

    while (v != Uset[v]) {
    v = Uset[v];//往父节点去找
    }

    return v;
    }

    //Kruskal
    //返回最小生成树的权值
    //
    //
    //初始化并查集(只需要数组存下标对应的父节点就行)_
    //遍布边集数组 一旦两个顶点的根不同，不是同一个集合
    // ，就放进同一个集合，（更新父节点）
    //开始操作 累计加上权值 记录到结果数组
    // 长此以往 直到遍布到 累加权值边的个数等于顶点数-1 就是最小生成树树
    //返回累加值
    int Kruskal(EdgeSet* edge, EdgeSet* result, MGraph* g,int edgeNum) {
    if (edge == NULL||result==NULL||g==NULL)return –1;
    //初始化并查集 每个节点只需要一个信息：它的父节点是谁
    int* Uset = malloc(sizeof(int) * g->nodeNum);
    if (Uset == NULL)return –1;
    memset(Uset, 0, sizeof(int) * g->nodeNum);
    for (int i = 0; i < g->nodeNum; i++)
    {
    Uset[i] = i;
    }

    int a, b;// 根
    int weightSum = 0;
    int cur = 0;//记录多少条边累加了已选择的边数

    //edgeNum是边的数量，而数组下标从0开始
    for (int i = 0; i < edgeNum ; i++)
    {
    a = findRoot(Uset, edge[i].vervex1);
    b = findRoot(Uset, edge[i].vervex2);

    if (a != b) {
    Uset[a] = b;

    result[cur].vervex1 = edge[i].vervex1;
    result[cur].vervex2 = edge[i].vervex2;
    result[cur].weight = edge[i].weight;
    cur++;

    weightSum += edge[i].weight;
    }

    // 当选择的边数等于节点数-1时，最小生成树已完成
    if (cur == g->nodeNum – 1) {
    break;
    }
    }

    free(Uset);

    return weightSum;
    }

    两个条件的含义

    g->nodeNum – 1

    // 最小生成树的边数 = 顶点数 – 1
    if (cur == g->nodeNum – 1) {
    break;
    }

    • 意义：最小生成树已经完成

    • 依据：对于一个连通图，最小生成树一定有 n-1 条边（n为顶点数）

    • 目的：提前结束算法，不再处理剩余的边

    edgeNum

    for (int i = 0; i < edgeNum ; i++)

    • 意义：遍历所有的边
    • 依据：需要检查每条边，看它是否属于最小生成树
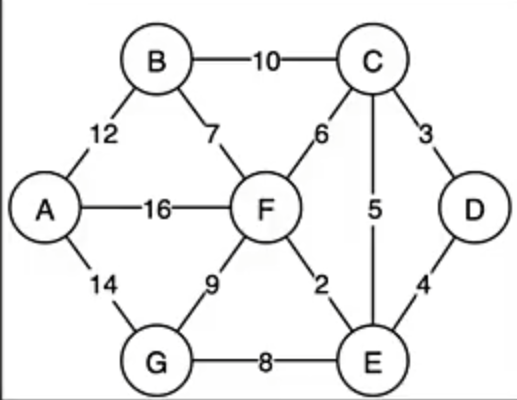
    • 目的：确保考虑了所有可能的边在这里插入图片描述

    最小生成树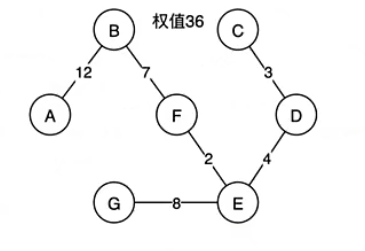在这里插入图片描述

    测试函数

    #include"Kruskal.h"
    #include<stdio.h>
    #include<stdlib.h>
    #include<string.h>
    #include"MGraph.h"

    static void testKruskal() {
    MGraph graph;
    const char* nodeName[] = { "A","B","C","D","E","F","G" };
    initMGraph(&graph, nodeName, 0, 0, sizeof(nodeName) / sizeof(nodeName[0]));

    addMGraphEdge(&graph , 0, 1, 12);
    addMGraphEdge(&graph , 0, 5, 16);
    addMGraphEdge(&graph, 0, 6, 14);
    addMGraphEdge(&graph, 1, 2, 10);
    addMGraphEdge(&graph, 1, 5, 7);
    addMGraphEdge(&graph, 2, 3, 3);
    addMGraphEdge(&graph, 2, 4, 5);
    addMGraphEdge(&graph, 2, 5, 6);
    addMGraphEdge(&graph, 3, 4, 4);
    addMGraphEdge(&graph, 4, 5, 2);
    addMGraphEdge(&graph, 4, 6, 8);
    addMGraphEdge(&graph, 5, 6, 9);

    EdgeSet* edge = createEdgeSet(graph.edgeNum);
    EdgeSet* result = createEdgeSet(graph.edgeNum);

    initEdgeSet(edge, &graph, graph.edgeNum);
    initEdgeSet(result, &graph, graph.edgeNum);

    sqrtEdgeSet(edge, graph.edgeNum);

    printf("最小权值和：%d\\n", Kruskal(edge, result, &graph, graph.edgeNum));

    //循环条件是graph.nodeNum-1 最小生成树的边个数为顶点-1
    for (int i = 0; i < graph.nodeNum–1 ; i++)
    {
    printf("%s———–%d———-%s\\n", graph.ver[result[i].vervex1].show,
    result[i].weight, graph.ver[result[i].vervex2].show);
    }

    if (edge) {
    free(edge);
    }
    if (result) {
    free(result);
    }

    }

    int main() {
    testKruskal();

    return 0;
    }

    所有代码

    邻接矩阵

    #pragma once
    #pragma once
    #define MAXNODENUM 20
    //节点结构
    typedef struct {
    int no;
    const char* show;//指针指向名字数组
    }MatrixVexNode;

    //边结构
    typedef int MatrixVexEdge;

    //图结构
    typedef struct {

    MatrixVexNode ver[MAXNODENUM];//顶点数组
    MatrixVexEdge edge[MAXNODENUM][MAXNODENUM];//矩阵
    //权重填在邻接矩阵里面
    int nodeNum;
    int edgeNum;
    int directed;
    }MGraph;

    //初始化图//多少个节点
    void initMGraph(MGraph* g, const char* nodename[], int edgeVaule, int directed, int num);
    //添加边//索引
    void addMGraphEdge(MGraph* g, int x, int y,int w);

    //遍布
    int MNodevisited[MAXNODENUM];//全局变量开始已经全0
    void DFSMGraphTravel(MGraph* g, int v);
    void initalizevisited();
    void BFSMGraphTravel(MGraph* g, int v);

    #include<stdio.h>
    #include<stdlib.h>
    #include<string.h>
    #include"MGraph.h"

    #define INF 1e4
    //初始化图//开始初始化为一个值表示没边//多少个节点
    void initMGraph(MGraph* g, const char* nodename[], int edgeVaule, int directed, int num) {
    if (g == NULL || nodename == NULL) {
    return;
    }
    memset(g, 0, sizeof(MGraph));
    g->directed = directed;
    g->edgeNum = 0;
    g->nodeNum = num;

    for (int i = 0; i < num; i++)
    {
    g->ver[i].no = i;
    g->ver[i].show = nodename[i];

    for (int j = 0; j < num; j++)
    {
    g->edge[i][j] = edgeVaule;
    }
    }

    }
    static int IsEdge(int w) {
    if (w > 0 && w < INF) {
    return 1;
    }
    return 0;
    }
    //一条条添加边//索引
    void addMGraphEdge(MGraph* g, int x, int y, int w) {
    if (g == NULL) {
    return;
    }

    if (x < 0 || x >= g->nodeNum || y < 0 || y >= g->nodeNum) {
    return;
    }
    //边而且权值合法而且没加过边过的情况下
    if (IsEdge(w))
    {
    g->edge[x][y] = w;
    g->edgeNum++;

    //如果无方向
    if (g->directed == 0) {
    g->edge[y][x] = w;
    }

    }

    }

    //遍布

    static void visitnode(const char* show) {
    printf("%s\\t", show);
    }
    //递归 避免死循环
    void DFSMGraphTravel(MGraph* g, int v) {
    if (g == NULL) {
    return;
    }
    if (v < 0 || v >= g->nodeNum) {
    return;
    }

    visitnode(g->ver[v].show);
    MNodevisited[v] = 1;

    for (int i = 0; i < g->nodeNum; i++)
    {
    if (MNodevisited[i] == 0 && IsEdge(g->edge[v][i])) {
    DFSMGraphTravel(g, i);
    }
    }
    }

    void initalizevisited() {
    for (int i = 0; i < MAXNODENUM; i++)
    {
    MNodevisited[i] = 0;
    }
    }

    //从某个顶点开始从距离近到远遍布
    //临时队列来写 下标
    // 入队时MNodevisited为1 出队遍布
    //1.创建队列2.激活队列入队
    void BFSMGraphTravel(MGraph* g, int v) {
    if (g == NULL) {
    return;
    }
    if (v < 0 || v >= g->nodeNum) {
    return;
    }
    //1.创建队列
    int queue[MAXNODENUM];
    int rear = 0; int front = 0;
    int cur = 0;//当前访问节点，为了遍布

    //2.激活队列入队
    queue[rear] = v;
    MNodevisited[v] = 1;
    rear = (rear + 1) % MAXNODENUM;

    for (int i = 0; i < g->nodeNum; i++)//出队列
    {
    //3.先出队自己， 出队再访问
    cur = queue[front];
    front = (front + 1) % MAXNODENUM;
    visitnode(g->ver[cur].show);

    for (int j = 0; j < g->nodeNum; j++)//遍布边
    {
    if (IsEdge(g->edge[cur][j]))
    {
    // 4.不断遍布所有可能的入队 沿着边
    if (MNodevisited[j] == 0) {
    queue[rear] = j;
    MNodevisited[j] = 1;
    rear = (rear + 1) % MAXNODENUM;
    }
    }
    }

    }
    }

    Kruskal

    #pragma once
    //根据邻接矩阵来生成边集数组
    #include"MGraph.h"
    typedef struct {
    int vervex1;
    int vervex2;
    int weight;
    }EdgeSet;

    //创建 传进来边的数量
    EdgeSet* createEdgeSet(int n);

    //初始化
    int initEdgeSet(EdgeSet* edge, MGraph* g, int num);

    //排序
    void sqrtEdgeSet(EdgeSet* edge, int edgeNum);

    //Kruskal
    //返回最小生成树的权值
    int Kruskal(EdgeSet* edge, EdgeSet* result, MGraph* g, int edgeNum);

    #include"Kruskal.h"
    #include<stdio.h>
    #include<stdlib.h>
    #include<string.h>

    //创建 传进来边的数量 n为邻接矩阵已经记录的边数量
    EdgeSet* createEdgeSet(int n) {
    EdgeSet* edge = malloc(n*sizeof(EdgeSet));
    if (edge == NULL)return NULL;
    memset(edge, 0, sizeof(EdgeSet));

    return edge;
    }

    //初始化
    //通过传进来的邻接矩阵来 初始化 边集数组
    //通过邻接矩阵的边的权值二维数组 约束条件 权值大于0
    //num 为顶点的数量
    //返回+1=边数量 (边集数组的索引+1)
    int initEdgeSet(EdgeSet* edge, MGraph* g, int num) {
    if (g == NULL|| edge ==NULL)return –1;

    int k = 0;//记录的边个数
    for (int i = 0; i < num; i++)
    {
    for (int j = i+1; j < num; j++)//i 0 j 1 i 1 j 2 i3j4
    {
    if (g->edge[i][j] > 0) {
    edge[k].vervex1 = i;
    edge[k].vervex2 = j;
    edge[k].weight = g->edge[i][j];
    k++;
    }
    }
    }

    return k;
    }

    //排序 选择排序
    //memcpy函数
    void sqrtEdgeSet(EdgeSet* edge,int edgeNum) {
    if (edge == NULL)return ;
    EdgeSettemp;

    for (int i = 0; i < edgeNum; i++)
    {
    for (int j = i+1; j < edgeNum; j++)
    {
    if (edge[j].weight < edge[i].weight) {
    memcpy(&temp, &edge[j], sizeof(EdgeSet));
    memcpy(&edge[j], &edge[i], sizeof(EdgeSet));
    memcpy(&edge[i], &temp, sizeof(EdgeSet));
    }
    }

    }
    }

    static int findRoot( int* Uset,int v) {
    if (Uset == NULL)return –1;

    while (v != Uset[v]) {
    v = Uset[v];//往父节点去找
    }

    return v;
    }

    //Kruskal
    //返回最小生成树的权值
    //
    //
    //初始化并查集(只需要数组存下标对应的父节点就行)_
    //遍布边集数组 一旦两个顶点的根不同，不是同一个集合
    // ，就放进同一个集合，（更新父节点）
    //开始操作 累计加上权值 记录到结果数组
    // 长此以往 直到遍布到 累加权值边的个数等于顶点数-1 就是最小生成树树
    //返回累加值
    int Kruskal(EdgeSet* edge, EdgeSet* result, MGraph* g,int edgeNum) {
    if (edge == NULL||result==NULL||g==NULL)return –1;
    //初始化并查集 每个节点只需要一个信息：它的父节点是谁
    int* Uset = malloc(sizeof(int) * g->nodeNum);
    if (Uset == NULL)return –1;
    memset(Uset, 0, sizeof(int) * g->nodeNum);
    for (int i = 0; i < g->nodeNum; i++)
    {
    Uset[i] = i;
    }

    int a, b;// 根
    int weightSum = 0;
    int cur = 0;//记录多少条边累加了已选择的边数

    for (int i = 0; i < edgeNum+1; i++)
    {
    a = findRoot(Uset, edge[i].vervex1);
    b = findRoot(Uset, edge[i].vervex2);

    if (a != b) {
    Uset[a] = b;

    result[cur].vervex1 = edge[i].vervex1;
    result[cur].vervex2 = edge[i].vervex2;
    result[cur].weight = edge[i].weight;
    cur++;

    weightSum += edge[i].weight;
    }

    // 当选择的边数等于节点数-1时，最小生成树已完成
    if (cur == g->nodeNum – 1) {
    break;
    }
    }

    free(Uset);

    return weightSum;
    }

    #include"Kruskal.h"
    #include<stdio.h>
    #include<stdlib.h>
    #include<string.h>
    #include"MGraph.h"

    static void testKruskal() {
    MGraph graph;
    const char* nodeName[] = { "A","B","C","D","E","F","G" };
    initMGraph(&graph, nodeName, 0, 0, sizeof(nodeName) / sizeof(nodeName[0]));

    addMGraphEdge(&graph , 0, 1, 12);
    addMGraphEdge(&graph , 0, 5, 16);
    addMGraphEdge(&graph, 0, 6, 14);
    addMGraphEdge(&graph, 1, 2, 10);
    addMGraphEdge(&graph, 1, 5, 7);
    addMGraphEdge(&graph, 2, 3, 3);
    addMGraphEdge(&graph, 2, 4, 5);
    addMGraphEdge(&graph, 2, 5, 6);
    addMGraphEdge(&graph, 3, 4, 4);
    addMGraphEdge(&graph, 4, 5, 2);
    addMGraphEdge(&graph, 4, 6, 8);
    addMGraphEdge(&graph, 5, 6, 9);

    EdgeSet* edge = createEdgeSet(graph.edgeNum);
    EdgeSet* result = createEdgeSet(graph.edgeNum);

    initEdgeSet(edge, &graph, graph.edgeNum);
    initEdgeSet(result, &graph, graph.edgeNum);

    sqrtEdgeSet(edge, graph.edgeNum);

    printf("最小权值和：%d\\n", Kruskal(edge, result, &graph, graph.edgeNum));

    //循环条件是graph.nodeNum-1 最小生成树的边个数为顶点-1

    for (int i = 0; i < graph.nodeNum–1 ; i++)
    {
    printf("%s———–%d———-%s\\n", graph.ver[result[i].vervex1].show,
    result[i].weight, graph.ver[result[i].vervex2].show);
    }

    if (edge) {
    free(edge);
    }
    if (result) {
    free(result);
    }

    }

    int main() {
    testKruskal();

    return 0;
    }

    赞(0)
    未经允许不得转载：网硕互联帮助中心 » 最小生成树：Kruskal算法(C语言)
    分享到： 更多 (0)
    标签：

    相关推荐

    评论 抢沙发

    评论前必须登录！

     

    热门标签

    服务器(4534)运维(2786)linux(1404)人工智能(804)java(688)网络(659)开发语言(585)python(558)c++(444)数据库(408)前端(405)美国站群服务器(308)香港云服务器(305)算法(304)租用香港服务器(301)香港服务器(298)香港站群服务器租用(298)租用香港站群服务器(294)香港服务器租用(293)香港站群服务器(289)美国云服务器(286)香港VPS(280)美国服务器租用(279)美国服务器(276)ubuntu(268)windows(266)docker(239)学习(225)安全(214)深度学习(211)

    置顶推荐

    热门文章

    最新文章