AtCoder Beginner Contest 418(补题) C

C题：

C – Flush

Time Limit: 2 sec / Memory Limit: 1024 MiB

Score : 350 points

Problem Statement

On the poker table, there are tea bags of N different flavors. The flavors are numbered from 1 through N, and there are Ai​ tea bags of flavor i (1≤i≤N).

You will play a game using these tea bags. The game has a parameter called difficulty between 1 and A1​+⋯+AN​, inclusive. A game of difficulty b proceeds as follows:

The dealer will do their best to make you lose.

You are given Q queries, so answer each of them. The j-th query is as follows:

• For a game of difficulty Bj​, report the minimum integer x you must declare at the start to guarantee a win. If it is impossible to win, report −1 instead.

Constraints

• 1≤N≤3×105
• 1≤Q≤3×105
• 1≤Ai​≤106 (1≤i≤N)
• 1≤Bj​≤min(106,A1​+⋯+AN​) (1≤j≤Q)
• All input values are integers.

Input

The input is given from Standard Input in the following format:

N Q
A1​ ⋯ AN​
B1​
⋮
BQ​

Output

Print Q lines.

The j-th line (1≤j≤Q) should contain the answer to the j-th query.

Sample Input 1

Copy

4 5
4 1 8 4
1
8
5
2
10

Sample Output 1

Copy

1
17
14
5
-1

For the 1-st query, if you declare x=1, then no matter which 1 bag the dealer chooses, you can satisfy the winning condition by choosing appropriate 1 bag among them. Since you cannot choose an integer x less than 1, the answer is 1.

For the 2-nd query, if you declare x=17, then no matter which 17 bags the dealer chooses, you can satisfy the winning condition by choosing appropriate 8 bags among them. Conversely, if x<17, the dealer can choose bags to prevent your victory. Thus, the answer is 17.

For the 3-rd query, if you declare x=14, then no matter which 14 bags the dealer chooses, you can satisfy the winning condition by choosing appropriate 5 bags among them. Conversely, if x<14, the dealer can choose bags to prevent your victory. Thus, the answer is 14.

For the 4-th query, if you declare x=5, then no matter which 5 bags the dealer chooses, you can satisfy the winning condition by choosing appropriate 2 bags among them. Conversely, if x<5, the dealer can choose bags to prevent your victory. Thus, the answer is 5.

For the 5-th query, no matter what x you declare, the dealer can choose bags to prevent your victory. Thus, print −1.

Sample Input 2

Copy

5 3
13 13 13 13 2
5
12
13

Sample Output 2

Copy

19
47
51

翻译：

C – Flush 

时间限制：2 秒 / 内存限制：1024 MiB

  得分： 350 分

  问题描述

在扑克桌上，有 N 种不同口味的茶包。这些口味的编号从 1 到 N ，其中有 Ai​ 个 i 口味的茶包（ 1≤i≤N ）。

你将使用这些茶包玩一个游戏。这个游戏有一个参数叫做难度，范围在 1 到 A1​+⋯+AN​ 之间（包括 1 和 A1​+⋯+AN​ ）。难度为 b 的游戏如下进行：

庄家会尽力让你输。

给你 Q 个查询，回答每一个查询。第 j 个查询如下：

• 对于难度为 Bj​ 的游戏，报告你必须从开始就声明的最小整数 x 以确保获胜。如果无法获胜，则报告 −1 。

  约束条件

• 1≤N≤3×105
• 1≤Q≤3×105
• 1≤Ai​≤106 (1≤i≤N)
• 1≤Bj​≤min(106,A1​+⋯+AN​) (1≤j≤Q)
• 所有输入值都是整数。

  输入

输入按照以下格式从标准输入给出：

N Q
A1​ ⋯ AN​
B1​
⋮
BQ​

  输出

  打印 Q 行。

第 j 行（ 1≤j≤Q ）应包含第 j 个查询的答案。

  示例输入 1Copy

  复制

4 5
4 1 8 4
1
8
5
2
10

  示例输出 1Copy

  复制

1
17
14
5
-1

对于第 1 个查询，如果你声明 x=1 ，那么无论经销商选择哪个 1 袋，你都可以通过选择其中合适的 1 袋来满足获胜条件。由于你不能选择小于 1 的整数 x ，所以答案是 1 。

对于第 2 个查询，如果你声明 x=17 ，那么无论经销商选择哪些 17 袋，你都可以通过选择其中合适的 8 袋来满足获胜条件。相反，如果 x<17 ，经销商可以选择袋子来阻止你的胜利。因此，答案是 17 。

对于第 3 个查询，如果你声明 x=14 ，那么无论经销商选择哪些 14 袋子，你都可以通过选择其中的适当 5 袋子来满足获胜条件。相反，如果 x<14 ，经销商可以选择袋子来阻止你的胜利。因此，答案是 14 。

对于第 4 个查询，如果你声明 x=5 ，那么无论经销商选择哪些 5 袋子，你都可以通过选择其中的适当 2 袋子来满足获胜条件。相反，如果 x<5 ，经销商可以选择袋子来阻止你的胜利。因此，答案是 5 。

对于第 5 个查询，无论你声明什么 x ，经销商都可以选择袋子来阻止你的胜利。因此，打印 −1 。

  示例输入 2Copy

  复制

5 3
13 13 13 13 2
5
12
13

  示例输出 2Copy

  复制

19
47
51

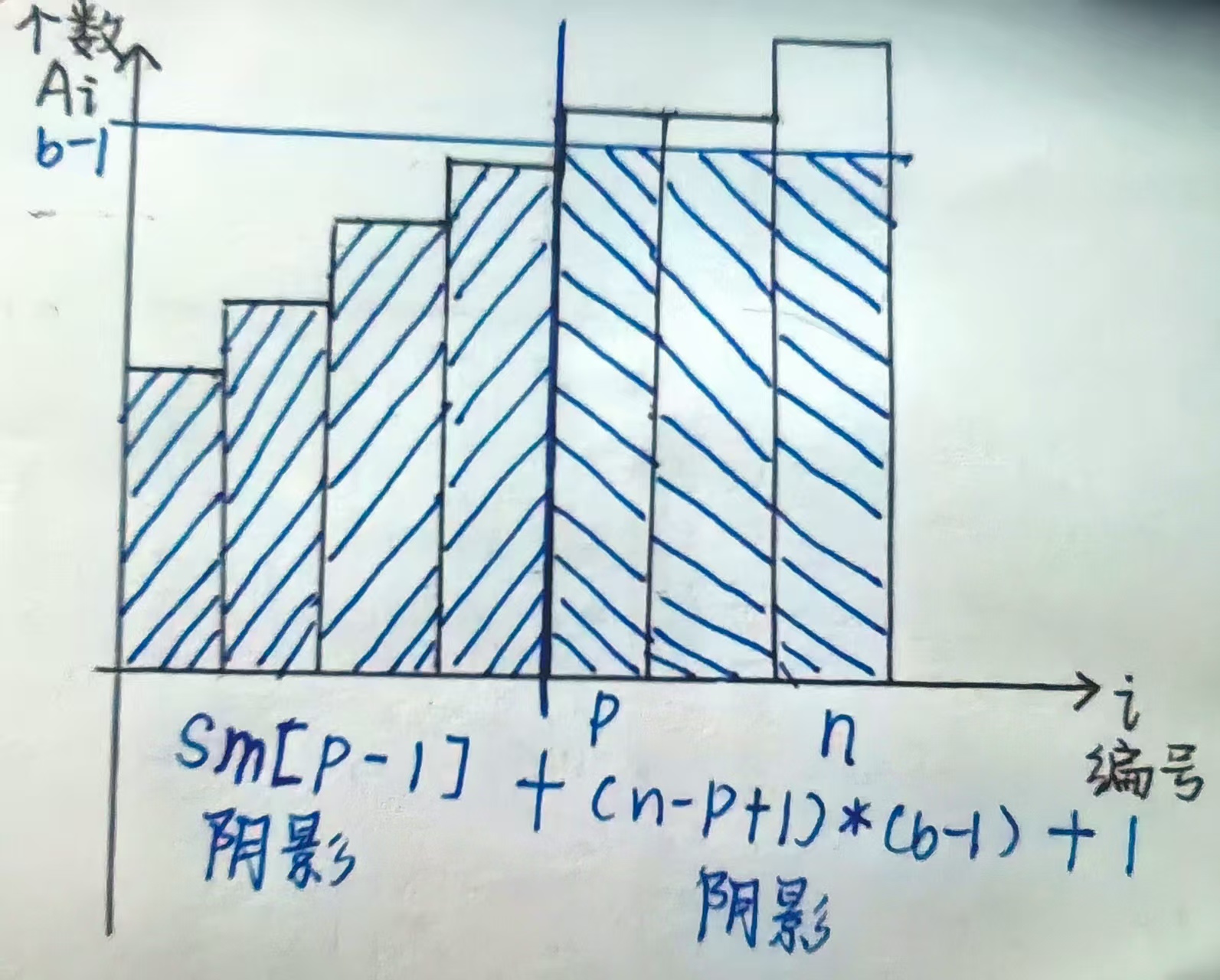
分析：使庄家胜利的x的最大值，加上1，就是“我”胜利所需的最小值，先将不同口味的茶包按个数从小到大排序，找到个数大于等于b-1的索引，索引之前相加，索引之后以（b-1）为高相乘，最后再加上1，即为最小值（参考讲解视频【AtCoder 初学者竞赛 418比赛讲解（ABC418）】https://www.bilibili.com/video/BV1HubKzkE42?vd_source=3454b81e777238fd36a1725a4c3b1790）

#include<iostream>
#include<algorithm>
using namespace std;
#define int long long
const int N = 3e5 + 5;
int q, n, a[N], sm[N];
signed main()
{
cin >> n >> q;
for (int i = 1;i <= n;++i)
{
cin >> a[i];
}
sort(a + 1, a + n + 1);
for (int i = 1;i <= n;++i)
{
sm[i] = sm[i – 1] + a[i];//前缀和
}
while (q–)
{
int b, ans=0;
cin >> b;
//找到大于等于b-1的元素地址，再减去首地址，得到坐标索引
int p = lower_bound(a + 1, a + 1 + n, b – 1)-a;
ans += sm[p – 1] + (n – p + 1) * (b – 1) + 1;
if (ans > sm[n])//满足条件的x比茶包总数还大，不合规
ans = -1;
cout << ans << endl;
}
return 0;
}