1 前言
笔者在做量产项目的过程中或者写博客的过程中会经常思考各种方案之间的优缺点,也算是一个总结,那么本次带来的话题就是:自动驾驶Motion Planning模块轨迹平滑方式。
笔者在之前的博客中 《自动驾驶—Motion Planning之轨迹Path优化》讲过离散点的轨迹平滑(Apollo中使用,目前了解到也有一些智驾公司使用这种方式),在博客《自动驾驶—Motion Planning之STSC轨迹优化》中讲解过多段bezier轨迹的平滑(也有其它智驾公司使用该算法)。
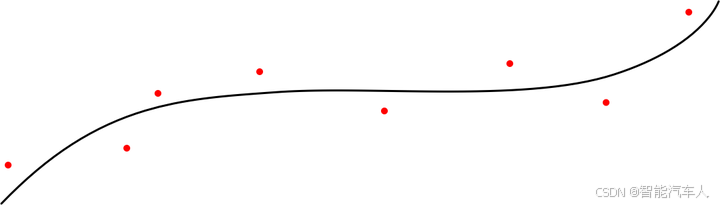
2 轨迹平滑
离散点的轨迹平滑和多段bezier轨迹的平滑,这两者有着相似的地方,也有不同的地方。
相同点包括:(1)都需要初始轨迹(2)都是构建二次规划问题求解;
不同点在于:(1)前者只能进行path的平滑,speed的平滑需要单独求解;而后者求解得到多段bezier曲线参数方程之后,即可得到path+speed等轨迹信息。(2)前者path求解只包括(x,y)或者(s,l)信息,其中轨迹的kappa信息需要单独计算;而后者中的bezier参数方程可直接kappa求解公式得到。
二次规划问题的构造,主要包括以下几个方面:
2.1 初始轨迹
两者都需要上游轨迹的输入(粗解),前者的输入是平滑后的参考线,而后者是 A* 求解得到的粗轨迹。
2.2 构建代价函数
前者:优化目标中主要考虑了(1)横向位移 (2)横向速度(3)横向加速度(4)横向Jerk(5)障碍物的距离。
后者:以s和l方向上的三阶导最小为优化目标函数。
2.3 约束构建
前者:(1)连续性(2)安全性等。
后者:(2)连续性(2)cube约束等。
2.4 求解
前者:求解的是l,l',l''的信息。
后者:求解的是Bezier曲线的控制点信息。
3 两种方案优缺点
3.1 离散点轨迹平滑
离散点的二次规划轨迹平滑是通过优化算法调整离散轨迹点的位置,使其满足平滑性约束和其他约束(如速度、加速度限制)。
(1)优点
-
灵活性:可以直接处理任意离散点,适用于不规则轨迹。
-
约束处理能力强:能够处理多种约束(如平滑性、避障、动力学约束)。
-
全局优化:通过优化算法实现全局平滑性。
(2)缺点
-
计算复杂度高:随着轨迹点数量增加,优化问题的规模增大,计算复杂度较高。
-
精度损失:约束条件精度损失(特别是非线性约束线性化)。
3.2 多段 Bezier 轨迹平滑
多段 Bezier 轨迹的平滑是指使用多段 Bezier 曲线拼接生成平滑轨迹,每段 Bezier 曲线由控制点定义。
(1)优点
-
高阶平滑性:Bezier 曲线天然具有高阶连续性(如 C2C2 连续性),适合高精度轨迹平滑。
-
全局性:通过优化控制点,可以实现全局平滑性。
-
约束处理能力强:Bezier 曲线的控制点可以灵活调整,适合处理复杂约束(如曲率约束、避障约束)。
(2)缺点
-
计算复杂度偏高:优化多段 Bezier 曲线的控制点需要较高的计算资源。
4 对比总结
| 输入 | 离散轨迹点 | 控制点(定义每段 Bezier 曲线) |
| 输出 | 优化后的平滑轨迹点 | 由多段 Bezier 曲线拼接的平滑轨迹 |
| 平滑性 | 通过优化实现全局平滑性 | 高阶平滑性(如 C2C2 连续性) |
| 约束处理 | 适合处理多种约束(如平滑性、避障) | 适合处理复杂约束(如曲率、避障) |
| 计算复杂度 | 一般(随着轨迹点数量增加) | 较高(优化控制点) |
| 实现难度 | 一般(需定义目标函数和约束条件) | 一般(需处理多段曲线拼接和连续性约束) |
 网硕互联帮助中心
网硕互联帮助中心



评论前必须登录!
注册