基于粒子群算法优化长短期记忆网络LSTM的风电场发电功率预测
文章目录
- 基于粒子群算法优化长短期记忆网络LSTM的风电场发电功率预测
-
- 1.LSTM原理
- 2.风电功率预测
- 2.1 数据集
- 3.基于粒子群算法优化的LSTM
- 4.实验结果
- 5.Matlab代码
1.LSTM原理
LSTM 模型主要引入了"门"的机制,其中包含三个门:遗忘门、输入门和输出门。通过这些门的组合,LSTM 能 够在序列中有效地存储和检索信息,从而更好地捕捉长期依赖关系。其结构如图 1 所示。
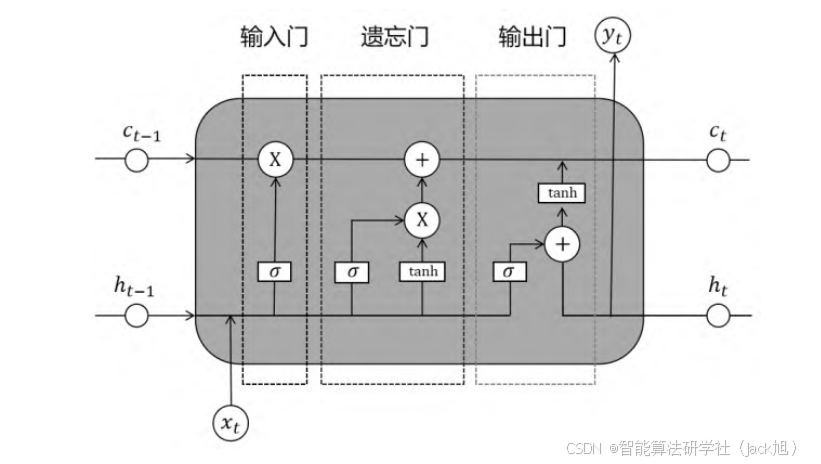
图 1 LSTM 模型的网络结构
当前状态与上一时刻状态关系为
f
t
=
σ
(
W
f
∙
[
h
t
−
1
,
x
t
]
+
b
f
)
i
t
=
σ
(
W
i
∙
[
h
t
−
1
,
x
t
]
+
b
i
)
C
~
t
=
tanh
(
W
c
∙
[
h
t
−
1
,
x
t
]
+
b
c
)
o
t
=
σ
(
W
o
∙
[
h
t
−
1
,
x
t
]
+
b
o
)
\\begin{aligned} & f_t=\\sigma\\left(W_f \\bullet\\left[h_{t-1}, x_t\\right]+b_f\\right) \\\\ & i_t=\\sigma\\left(W_i \\bullet\\left[h_{t-1}, x_t\\right]+b_i\\right) \\\\ & \\tilde{C}_t=\\tanh \\left(W_c \\bullet\\left[h_{t-1}, x_t\\right]+b_c\\right) \\\\ & o_t=\\sigma\\left(W_o \\bullet\\left[h_{t-1}, x_t\\right]+b_o\\right) \\end{aligned}
ft=σ(Wf∙[ht−1,xt]+bf)it=σ(Wi∙[ht−1,xt]+bi)C~t=tanh(Wc∙[ht−1,xt]+bc)ot=σ(Wo∙[ht−1,xt]+bo)
式中:
σ
\\sigma
σ 为 sigmod 激活函数;
tanh
\\tanh
tanh 为双曲正切激活函数;
h
t
−
1
h_{t-1}
ht−1 为
t
−
1
\\mathrm{t}-1
t−1 时刻的输出;
f
t
,
i
t
,
C
~
t
,
o
t
f_t, ~ i_t, ~ \\tilde{C}_t, ~ o_t
ft, it, C~t, ot 分别为 :t时刻下遗忘门限,输入门限,状态矩阵,输出门限;
W
f
,
W
i
,
W
c
,
W
o
W_f, ~ W_i, ~ W_c, ~ W o
Wf, Wi, Wc, Wo 分别为各对应层的权重t;
b
f
,
b
i
,
b
c
,
b
o
b_f, ~ b_i, ~ b_c, ~ b_o
bf, bi, bc, bo分别为各对应层的偏置系数。
最后,新的状态表示为
C
t
=
f
t
×
c
t
−
1
+
i
t
×
C
~
t
C_t=f_t \\times c_{t-1}+i_t \\times \\tilde{C}_t
Ct=ft×ct−1+it×C~t
2.风电功率预测
2.1 数据集
数据集为2019年风电功率数据,数据集如下:
| 2019-01-01 00:00:00 | 0.223 | 0 | 0 | 0.818 | 0.818 | 166.816 | 177.355 | 6.224 | 210.836 | 210.836 | -13.154 | 898.71 | 53.497 | 0.979591 |
数据特征除时间意外,一共包含14维特征
我们利用Windowsize = 5天的数据预测下一天的数据, 于是5天的数据一共包含14*5=70维度,预测输出1维数据,即实际发电功率(mw)。实际应用中,Windowsize的大小可根据实际情况进行修改。
3.基于粒子群算法优化的LSTM
粒子群算法原理请参考:网络博客 由前文可知,LSTM的参数设置具有满目性。本文利用粒子群算法对LSTM的参数(学习率,LSTM神经元个数,正则化参数)进行优化。适应度函数设计为训练集的MAPE平均百分比误差:
f
i
t
n
e
s
s
=
a
r
g
m
i
n
(
M
A
P
E
p
r
i
d
e
c
t
)
fitness = argmin(MAPE{pridect})
fitness=argmin(MAPEpridect)
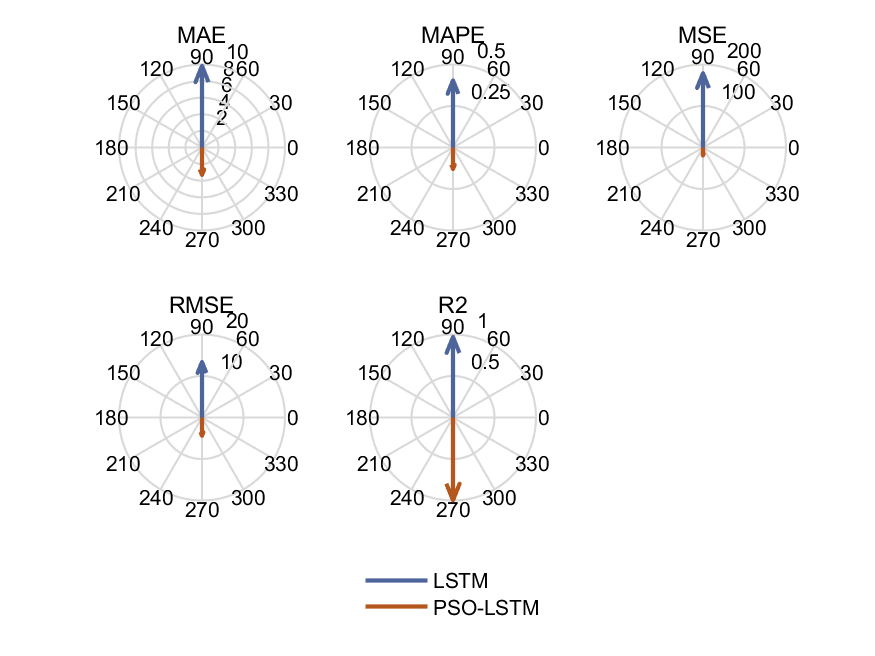
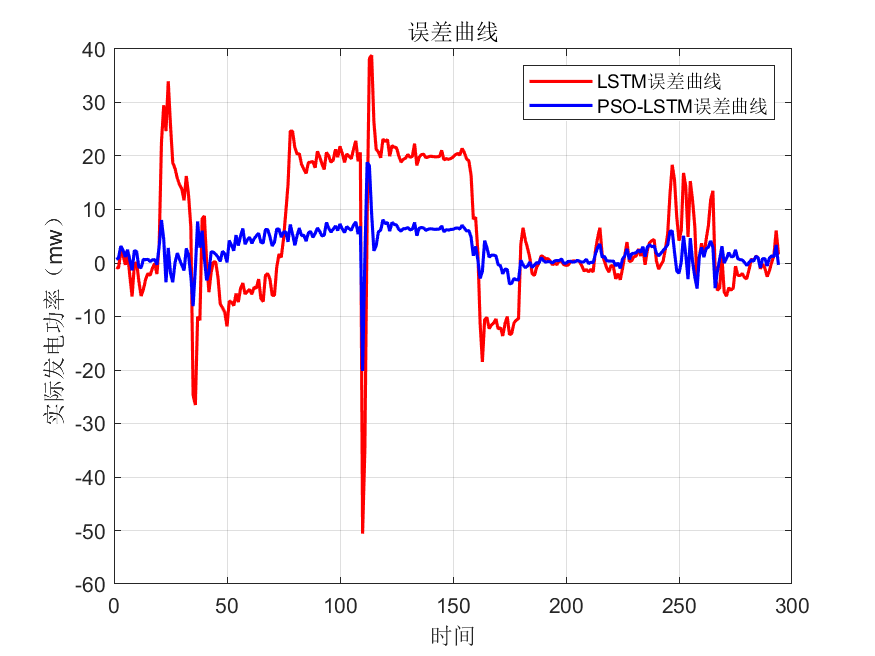
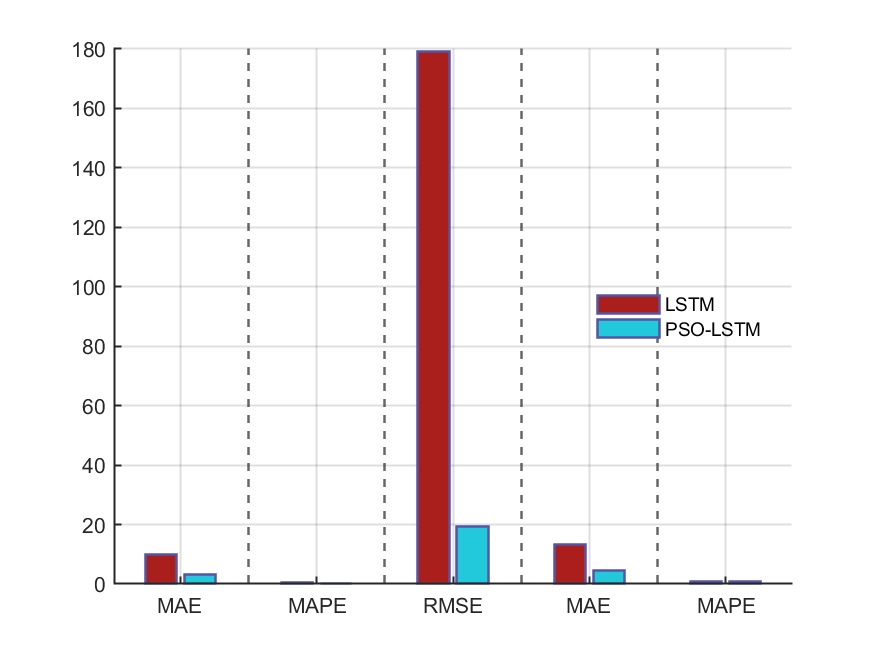
适应度函数选取训练后的MAPE误差。MAPE误差越小表明预测的数据与原始数据重合度越高。最终优化的输出为最佳学习率,LSTM神经元个数,正则化参数。然后利用最佳学习率,LSTM神经元个数,正则化参数训练后的网络对测试数据集进行测试。
4.实验结果
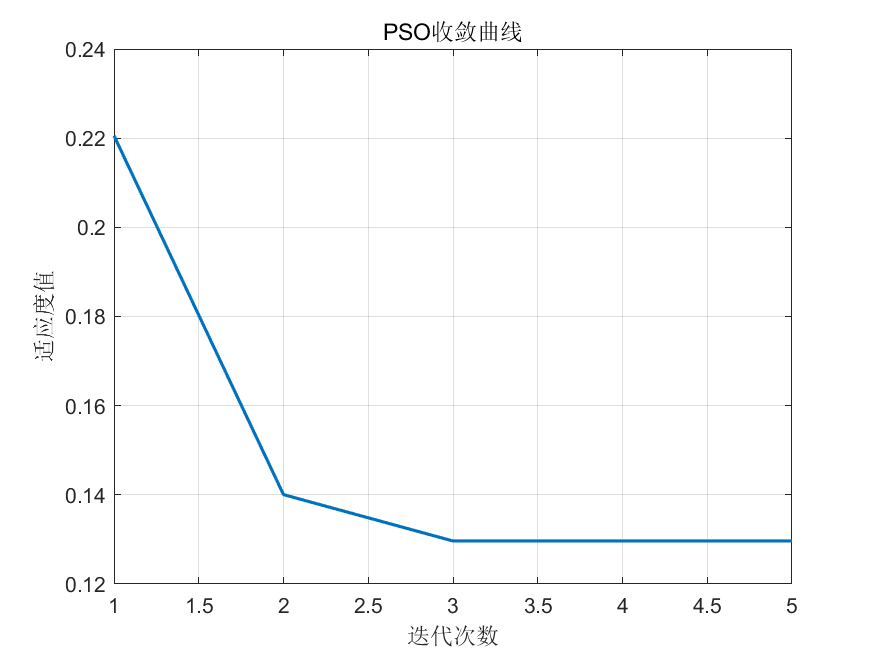
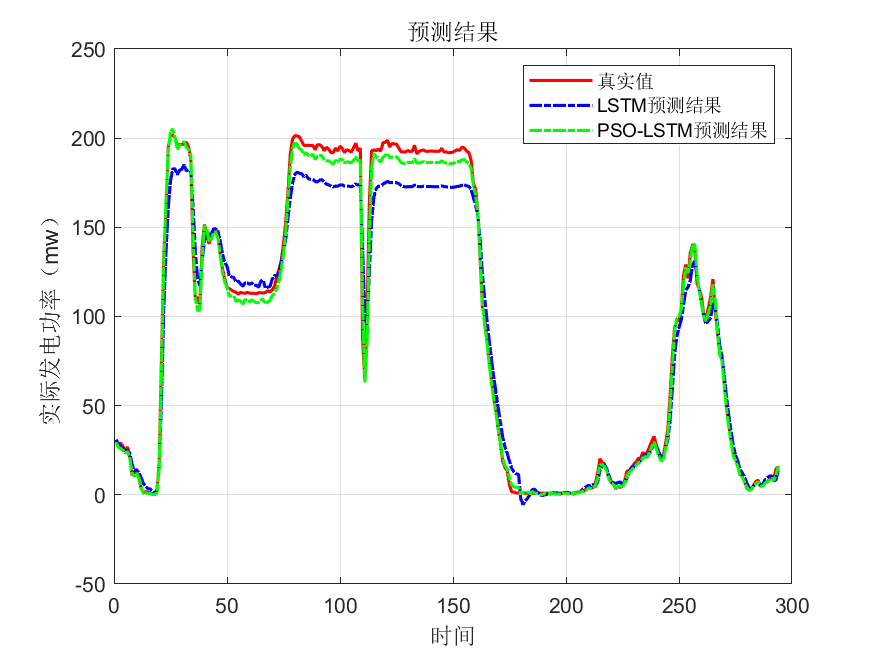
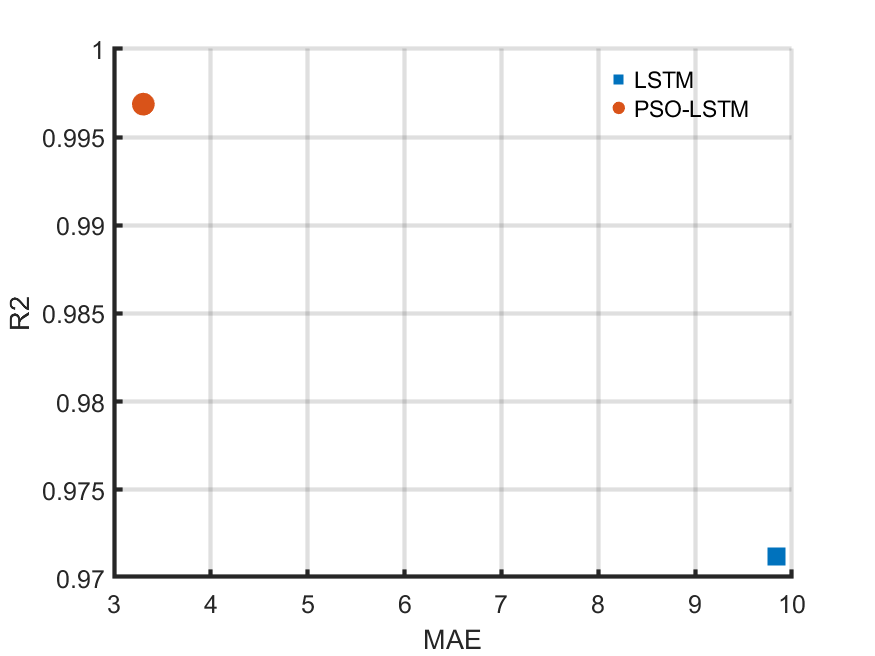
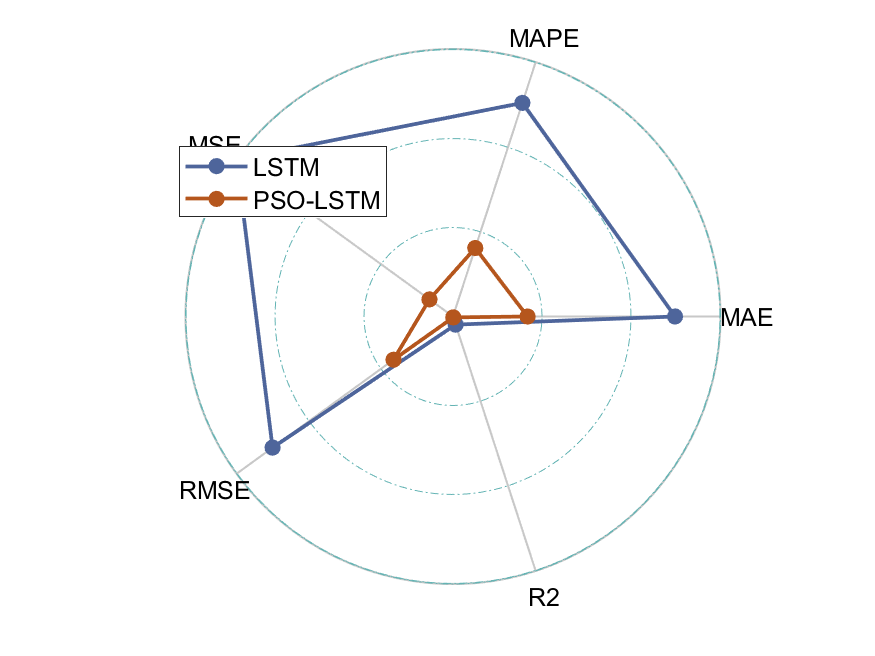
 网硕互联帮助中心
网硕互联帮助中心


评论前必须登录!
注册