在算法的幽深回廊中,链表以简洁的指针结构编织着数据的迷宫。当两条孤链在内存中悄然交汇,或是节点序列暗藏回文密码时,一场关于空间与时间的精密博弈便悄然上演。今日,我们以双指针为刃,剖开「链表相交」的拓扑谜题;再借快慢指针之力,破解「回文链表」的对称玄机——不写一行代码,纯享算法设计的思维风暴。
问题一:链表相交——内存拓扑的邂逅
给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表没有交点,返回 null 。
图示两个链表在节点 c1 开始相交:
题目数据 保证 整个链式结构中不存在环。
注意,函数返回结果后,链表必须 保持其原始结构 。
▍ 问题本质与约束
给定两条无环单链表 headA 和 headB,若存在共享子链(物理内存相同),需返回相交节点;否则返回 null。关键约束:
-
拓扑守恒:不可修改链表结构(如反转、破坏链接)。
-
时空敏感:节点数达 3×1043×104,需规避 O(n2)O(n2) 暴力扫描。
▍ 算法策略:双指针的路径调和
哈希表法(空间换时间)
-
原理:遍历链表A,节点存入哈希表;遍历链表B,首个存在于哈希表的节点即为交点。
-
复杂度:时间 O(m+n)O(m+n),空间 O(m)O(m) 或 O(n)O(n)。
-
缺陷:空间复杂度违反本题理想解要求(尽管题目未明示,但最优解应追求 O(1)O(1) 空间)。
双指针路径调和法(最优解)
-
核心洞察:若两链相交,头节点到交点的路径差可被消除。
-
操作流程:
-
指针 pA 遍历链表A,指针 pB 遍历链表B。
-
当 pA 达尾节点时,跳至 headB 继续;当 pB 达尾节点时,跳至 headA 继续。
-
若相交,pA 和 pB 必在交点相遇(路径长度均为 m+n−km+n−k,k为共享链长度);若不相交,最终同步指向 null。
-
-
复杂度:时间 O(m+n)O(m+n),空间 O(1)O(1)。
▶ 示例推演(示例1)
A: 4→1→8→4→5
B: 5→0→1→8→4→5
-
pA 路径:4→1→8 (交点) →4→5→跳至B头→5→0→1→8 (相遇点)
-
pB 路径:5→0→1→8 (交点) →4→5→跳至A头→4→1→8 (相遇点)
题目程序:
#include <stdio.h>
#include <stdlib.h>
// 定义链表节点结构
struct ListNode {
int val; // 节点存储的值
struct ListNode *next; // 指向下一个节点的指针
};
// 查找两个链表相交节点的函数
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) {
// 初始化两个指针,分别指向两个链表的头部
struct ListNode *pA = headA;
struct ListNode *pB = headB;
// 当两个指针不相交时继续遍历
while (pA != pB) {
// 如果pA到达链表A末尾,则跳转到链表B头部
pA = (pA == NULL) ? headB : pA->next;
// 如果pB到达链表B末尾,则跳转到链表A头部
pB = (pB == NULL) ? headA : pB->next;
}
// 返回相交节点(若不相交则返回NULL)
return pA;
}
// 创建新节点的辅助函数
struct ListNode *createNode(int val) {
// 动态分配内存创建新节点
struct ListNode *node = (struct ListNode *)malloc(sizeof(struct ListNode));
node->val = val; // 设置节点值
node->next = NULL; // 初始化next指针为NULL
return node; // 返回新节点指针
}
// 释放链表内存的辅助函数
void freeList(struct ListNode *head) {
// 遍历链表释放所有节点内存
while (head != NULL) {
struct ListNode *temp = head; // 临时保存当前节点
head = head->next; // 移动到下一个节点
free(temp); // 释放当前节点内存
}
}
int main() {
// ========== 创建测试链表 ==========
// 创建链表A:4 → 1 → 8 → 4 → 5
struct ListNode *headA = createNode(4);
headA->next = createNode(1);
headA->next->next = createNode(8);
headA->next->next->next = createNode(4);
headA->next->next->next->next = createNode(5);
// 创建链表B:5 → 0 → 1
struct ListNode *headB = createNode(5);
headB->next = createNode(0);
headB->next->next = createNode(1);
// 让链表B的第三个节点指向链表A的第三个节点(值为8的节点)
headB->next->next->next = headA->next->next;
// ========== 查找相交节点 ==========
struct ListNode *intersection = getIntersectionNode(headA, headB);
// ========== 打印结果 ==========
if (intersection != NULL) {
printf("Intersected at node with value: %d\\n", intersection->val);
} else {
printf("No intersection found\\n");
}
// ========== 清理内存 ==========
// 注意:只释放链表A和B的非共享部分
struct ListNode *temp = headB->next->next->next; // 保存共享节点地址
headB->next->next->next = NULL; // 断开链表B与共享部分的连接
freeList(headA); // 释放链表A(包含共享部分)
freeList(headB); // 释放链表B(不包含共享部分)
return 0;
}
输出结果: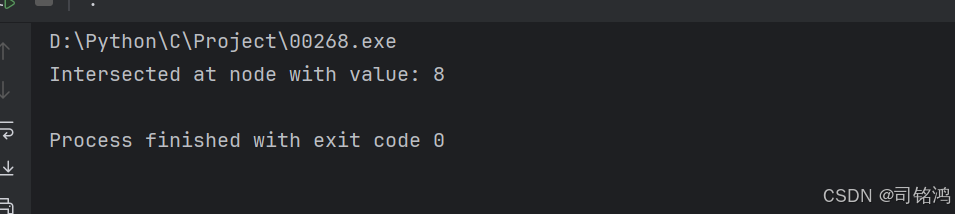
问题二:回文链表——时空约束下的对称审判
编写一个函数,检查输入的链表是否是回文的。但必须用 O(n) 时间复杂度和 O(1) 空间复杂度解决此题
▍ 问题本质与约束
验证单链表是否为回文序列,要求:
-
时间复杂度 O(n)O(n):禁止多次遍历。
-
空间复杂度 O(1)O(1):禁用栈、数组等额外存储。
▍ 算法策略:快慢指针与局部反转
快慢指针定位中点
-
快指针 fast 每次移动两步,慢指针 slow 移动一步。
-
当 fast 达末尾时,slow 指向链表中点(偶数为左中点)。
反转后半链表
-
从中点开始反转后半部分节点,生成新链 reversed。
-
关键操作:修改节点指针方向,不占用额外空间。
双指针比对序列
-
指针 p1 从头部开始,p2 从 reversed 头部开始。
-
依次比对 p1.val 与 p2.val,若全部相同则为回文。
恢复链表结构(可选)
-
再次反转后半部分,恢复原始拓扑。
▶ 示例推演(示例2)
原链: 1 → 2 → 2 → 1
1. 快慢指针:slow 停于第2个节点(值2)
2. 反转后半:2 → 1 反转为 1 → 2
3. 比对:
– p1: 1 → 2 → …
– p2: 1 → 2 → …
– 两两相同,确认为回文。
题目程序:
#include <stdio.h> // 包含标准输入输出库
#include <stdlib.h> // 包含内存分配等标准库函数
// 定义链表节点结构
struct ListNode {
int val; // 节点存储的整数值
struct ListNode *next; // 指向下一个节点的指针
};
// 反转链表的函数
struct ListNode* reverseList(struct ListNode* head) {
struct ListNode *prev = NULL; // 前驱节点指针,初始化为NULL
struct ListNode *curr = head; // 当前节点指针,初始化为链表头
// 遍历链表进行反转
while (curr != NULL) {
struct ListNode *nextTemp = curr->next; // 临时保存下一个节点
curr->next = prev; // 当前节点指向前驱节点(反转操作)
prev = curr; // 前驱节点前进到当前节点
curr = nextTemp; // 当前节点前进到下一个节点
}
return prev; // 返回反转后的新头节点
}
// 检查链表是否为回文的函数
int isPalindrome(struct ListNode* head) {
// 处理空链表或单节点链表的情况
if (head == NULL || head->next == NULL) {
return 1; // 空链表或单节点链表默认为回文
}
// 初始化快慢指针
struct ListNode *slow = head; // 慢指针,每次移动一步
struct ListNode *fast = head; // 快指针,每次移动两步
// 使用快慢指针找到链表中点
while (fast->next != NULL && fast->next->next != NULL) {
slow = slow->next; // 慢指针前进一步
fast = fast->next->next; // 快指针前进两步
}
// 反转链表的后半部分
struct ListNode *secondHalf = reverseList(slow->next); // 从中点后开始反转
struct ListNode *firstHalf = head; // 前半部分从头开始
struct ListNode *secondHalfCopy = secondHalf; // 保存反转后链表的头指针(用于后续恢复)
int result = 1; // 结果标志,初始假设是回文
// 比较前半部分和反转后的后半部分
while (secondHalf != NULL) {
if (firstHalf->val != secondHalf->val) {
result = 0; // 发现不匹配,设置结果为非回文
break; // 提前结束比较
}
firstHalf = firstHalf->next; // 前半部分指针前移
secondHalf = secondHalf->next; // 后半部分指针前移
}
// 恢复链表原始结构(再次反转后半部分)
slow->next = reverseList(secondHalfCopy); // 将反转的后半部分再次反转恢复
return result; // 返回最终结果
}
// 创建新节点的辅助函数
struct ListNode* createNode(int val) {
struct ListNode *node = (struct ListNode*)malloc(sizeof(struct ListNode)); // 分配内存
node->val = val; // 设置节点值
node->next = NULL; // 初始化next指针为NULL
return node; // 返回新节点指针
}
// 释放链表内存的辅助函数
void freeList(struct ListNode* head) {
while (head != NULL) {
struct ListNode *temp = head; // 临时保存当前节点
head = head->next; // 移动到下一个节点
free(temp); // 释放当前节点内存
}
}
// 打印链表的辅助函数
void printList(struct ListNode* head) {
struct ListNode *current = head; // 当前节点指针
while (current != NULL) {
printf("%d -> ", current->val); // 打印节点值
current = current->next; // 移动到下一个节点
}
printf("NULL\\n"); // 打印链表结束标记
}
int main() {
// ====== 测试用例1:回文链表(奇数个节点)1->2->3->2->1 ======
struct ListNode *head1 = createNode(1);
head1->next = createNode(2);
head1->next->next = createNode(3);
head1->next->next->next = createNode(2);
head1->next->next->next->next = createNode(1);
printf("链表1: ");
printList(head1); // 打印链表
// 检查是否为回文并打印结果
if (isPalindrome(head1)) {
printf("链表1是回文链表\\n");
} else {
printf("链表1不是回文链表\\n");
}
// 验证链表结构已恢复
printf("恢复后的链表1: ");
printList(head1);
freeList(head1); // 释放内存
// ====== 测试用例2:回文链表(偶数个节点)1->2->2->1 ======
struct ListNode *head2 = createNode(1);
head2->next = createNode(2);
head2->next->next = createNode(2);
head2->next->next->next = createNode(1);
printf("\\n链表2: ");
printList(head2); // 打印链表
// 检查是否为回文并打印结果
if (isPalindrome(head2)) {
printf("链表2是回文链表\\n");
} else {
printf("链表2不是回文链表\\n");
}
// 验证链表结构已恢复
printf("恢复后的链表2: ");
printList(head2);
freeList(head2); // 释放内存
// ====== 测试用例3:非回文链表 1->2->3->4 ======
struct ListNode *head3 = createNode(1);
head3->next = createNode(2);
head3->next->next = createNode(3);
head3->next->next->next = createNode(4);
printf("\\n链表3: ");
printList(head3); // 打印链表
// 检查是否为回文并打印结果
if (isPalindrome(head3)) {
printf("链表3是回文链表\\n");
} else {
printf("链表3不是回文链表\\n");
}
// 验证链表结构已恢复
printf("恢复后的链表3: ");
printList(head3);
freeList(head3); // 释放内存
// ====== 测试用例4:单个节点链表 ======
struct ListNode *head4 = createNode(1);
printf("\\n链表4: ");
printList(head4); // 打印链表
// 检查是否为回文并打印结果
if (isPalindrome(head4)) {
printf("链表4是回文链表\\n");
} else {
printf("链表4不是回文链表\\n");
}
freeList(head4); // 释放内存
return 0; // 程序正常结束
}
输出结果: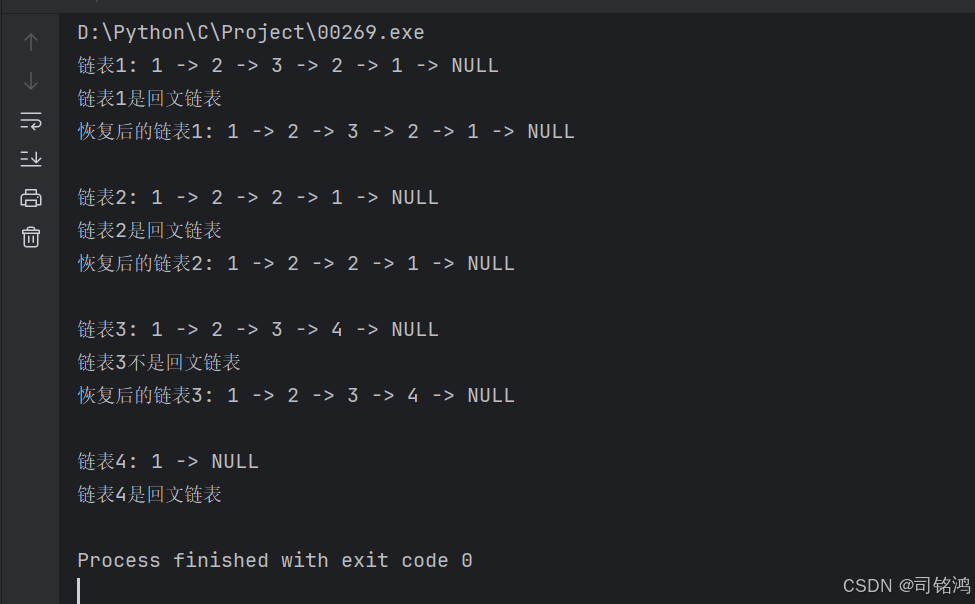
双雄争锋:算法策略对比图谱
| 核心目标 | 探测拓扑交点 | 验证序列对称性 |
| 关键约束 | 保持原始结构 | O(n)O(n) 时间 + O(1)O(1) 空间 |
| 核心算法 | 双指针路径长度补偿 | 快慢指针分区 + 局部反转 |
| 时间复杂度 | O(m+n)O(m+n) | O(n)O(n) |
| 空间复杂度 | O(1)O(1) | O(1)O(1) |
| 思维突破点 | 消除路径差的艺术 | 时间与空间的共生优化 |
总结:指针美学的二重奏
-
链表相交 是空间协作的哲学:通过路径长度的动态调和,双指针在内存迷宫中实现精准定位,揭示了算法中的“相遇是精心设计的必然”。
-
回文链表 是时间与对称的共舞:在苛刻的时空约束下,快慢指针切割时间,局部反转重塑空间,将对称验证转化为一场原地操作的芭蕾。
链表的灵魂在指针,算法的精髓在权衡。当相交问题以路径长度弥合差异,回文问题以局部反转重构对称时,我们看到的不仅是解法的巧妙,更是计算机科学中时空统一性的绝美体现。
博客结语
下一次当你面对纠缠的链表时,请记住:指针不仅是地址的向导,更是时空的诗人——它们在内存的舞台上,用相遇讲述协作,用反转书写对称。算法之美,尽在这动静之间。
 网硕互联帮助中心
网硕互联帮助中心


评论前必须登录!
注册