引言
单源最短路径问题是图论中的核心问题之一,旨在求解从图中一个特定源节点到其他所有节点的最短路径。这一问题在导航系统、网络路由、交通规划等领域有着广泛应用。本章将详细解析《算法导论》第 24 章介绍的四种经典算法,并提供完整可运行的 C++ 实现代码。
24.1 Bellman-Ford 算法
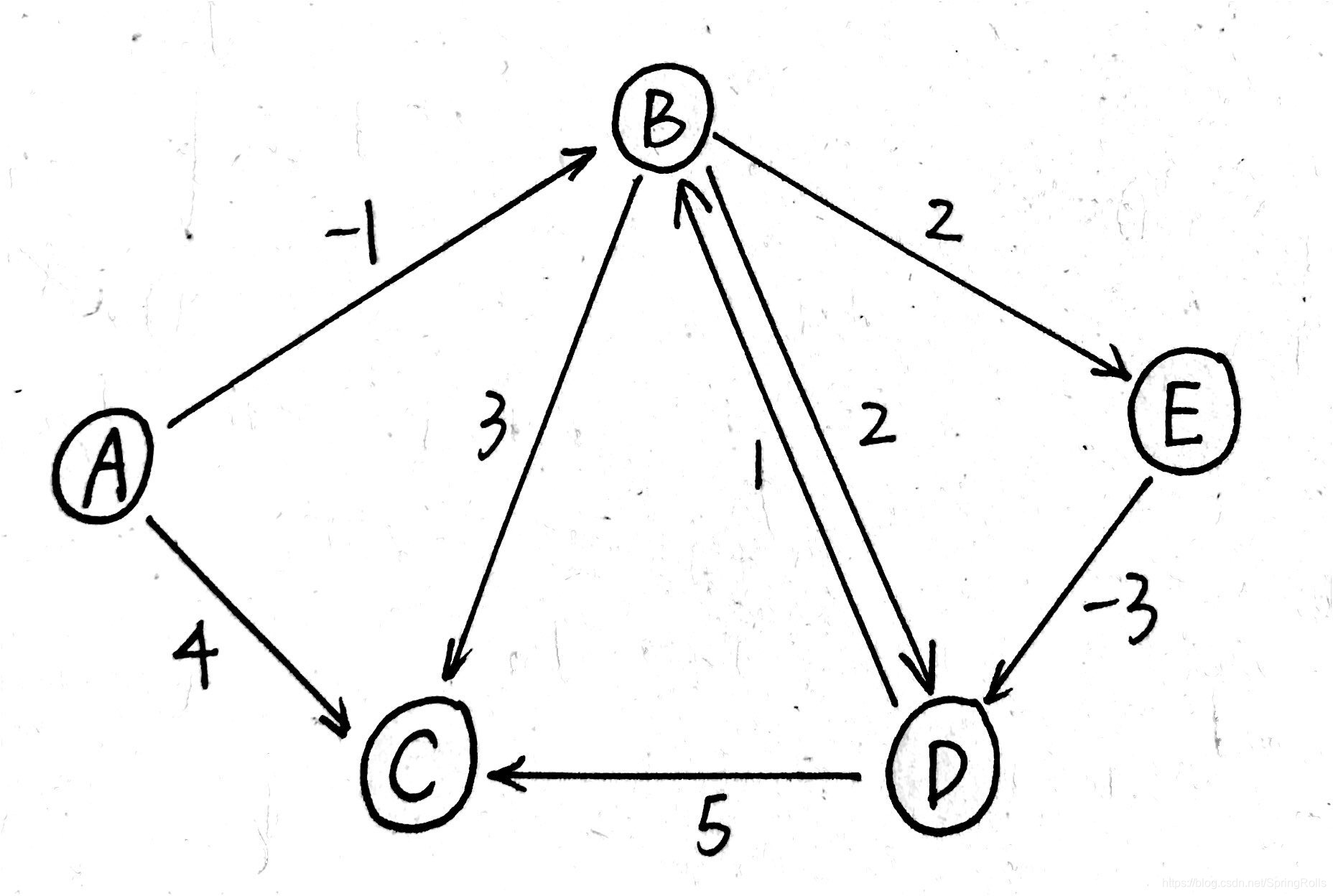
Bellman-Ford 算法是求解单源最短路径问题的经典算法,它能够处理包含负权边的图,并且可以检测出图中是否存在从源节点可达的负权回路。
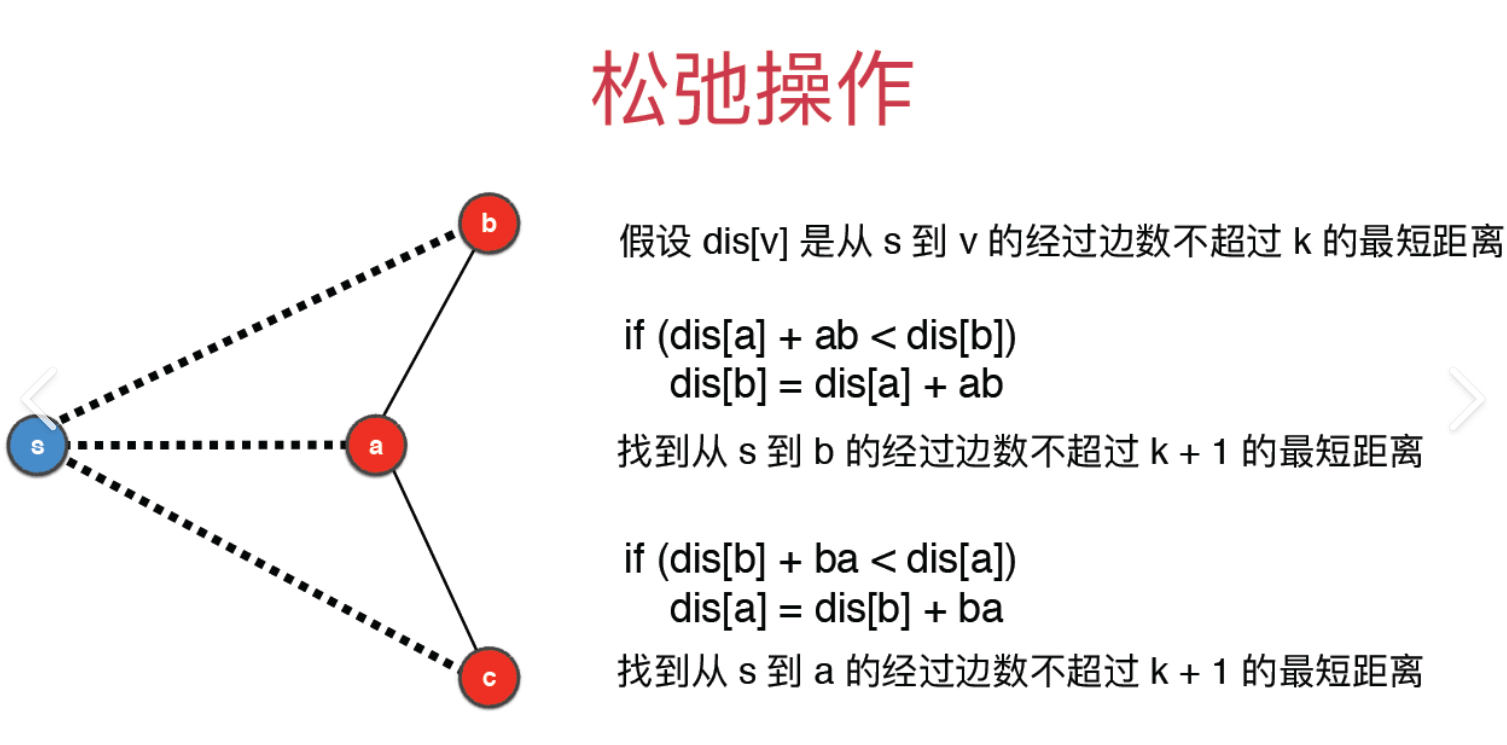
算法思想
代码实现
#include <iostream>
#include <vector>
#include <climits>
using namespace std;
// 边的结构体
struct Edge {
int u; // 起点
int v; // 终点
int weight; // 权重
Edge(int u_, int v_, int weight_) : u(u_), v(v_), weight(weight_) {}
};
/**
* Bellman-Ford算法实现
* @param edges 边的集合
* @param V 节点数量
* @param s 源节点
* @param distance 存储最短距离的数组
* @return 是否存在负权回路
*/
bool bellmanFord(const vector<Edge>& edges, int V, int s, vector<int>& distance) {
// 1. 初始化距离
distance.assign(V, INT_MAX);
distance[s] = 0;
// 2. 进行V-1次松弛操作
for (int i = 1; i <= V – 1; ++i) {
bool updated = false;
for (const Edge& e : edges) {
if (distance[e.u] != INT_MAX && distance[e.v] > distance[e.u] + e.weight) {
distance[e.v] = distance[e.u] + e.weight;
updated = true;
}
}
// 如果没有更新,可以提前退出
if (!updated) break;
}
// 3. 检测负权回路
for (const Edge& e : edges) {
if (distance[e.u] != INT_MAX && distance[e.v] > distance[e.u] + e.weight) {
return true; // 存在负权回路
}
}
return false; // 不存在负权回路
}
int main() {
// 示例图: 包含5个节点(0-4)
int V = 5;
vector<Edge> edges;
// 添加边
edges.emplace_back(0, 1, -1);
edges.emplace_back(0, 2, 4);
edges.emplace_back(1, 2, 3);
edges.emplace_back(1, 3, 2);
edges.emplace_back(1, 4, 2);
edges.emplace_back(3, 1, 1);
edges.emplace_back(3, 2, 5);
edges.emplace_back(4, 3, -3);
int source = 0;
vector<int> distance;
bool hasNegativeCycle = bellmanFord(edges, V, source, distance);
if (hasNegativeCycle) {
cout << "图中存在负权回路" << endl;
} else {
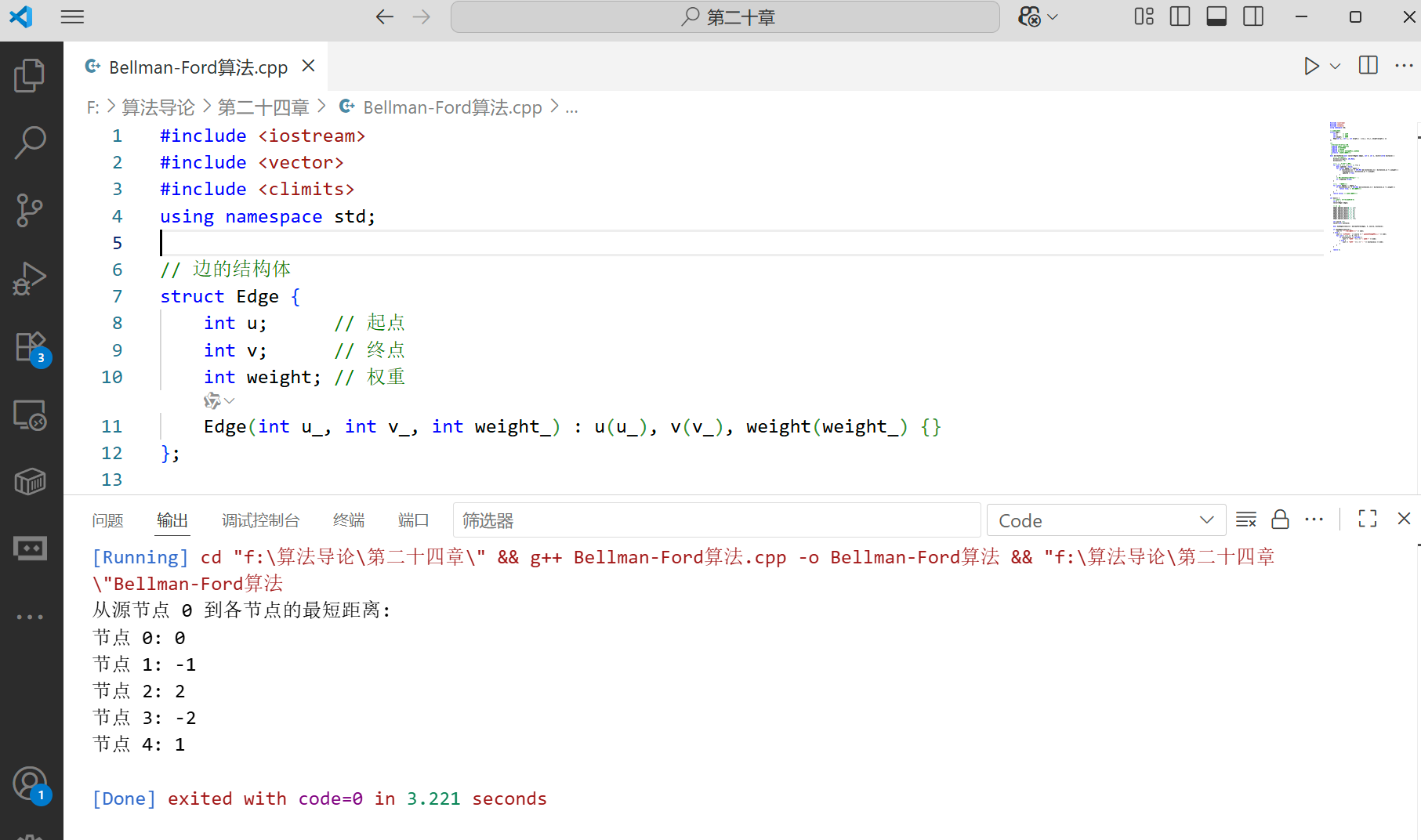
cout << "从源节点 " << source << " 到各节点的最短距离:" << endl;
for (int i = 0; i < V; ++i) {
if (distance[i] == INT_MAX) {
cout << "节点 " << i << ": 不可达" << endl;
} else {
cout << "节点 " << i << ": " << distance[i] << endl;
}
}
}
return 0;
}
综合案例及应用
下面是一个物流路径规划的案例,展示如何使用 Bellman-Ford 算法处理可能包含负权边(如折扣路线)的场景:
#include <iostream>
#include <vector>
#include <climits>
#include <string>
using namespace std;
struct Edge {
int from;
int to;
int cost; // 可以是负数,表示折扣
Edge(int f, int t, int c) : from(f), to(t), cost(c) {}
};
bool bellmanFord(const vector<Edge>& edges, int V, int s, vector<int>& distance, vector<int>& parent) {
distance.assign(V, INT_MAX);
parent.assign(V, -1);
distance[s] = 0;
for (int i = 1; i <= V – 1; ++i) {
for (const Edge& e : edges) {
if (distance[e.from] != INT_MAX && distance[e.to] > distance[e.from] + e.cost) {
distance[e.to] = distance[e.from] + e.cost;
parent[e.to] = e.from;
}
}
}
for (const Edge& e : edges) {
if (distance[e.from] != INT_MAX && distance[e.to] > distance[e.from] + e.cost) {
return true;
}
}
return false;
}
// 打印从源节点到目标节点的路径
void printPath(int target, const vector<int>& parent) {
if (parent[target] == -1) {
cout << target;
return;
}
printPath(parent[target], parent);
cout << " -> " << target;
}
int main() {
// 物流网络: 5个仓库节点(0-4)
int V = 5;
vector<Edge> edges;
// 添加运输路线及成本(负数表示折扣)
edges.emplace_back(0, 1, 10); // 仓库0到1,成本10
edges.emplace_back(0, 2, 30); // 仓库0到2,成本30
edges.emplace_back(0, 3, 100); // 仓库0到3,成本100
edges.emplace_back(1, 2, 5); // 仓库1到2,成本5
edges.emplace_back(2, 3, 20); // 仓库2到3,成本20
edges.emplace_back(3, 4, 10); // 仓库3到4,成本10
edges.emplace_back(2, 4, 60); // 仓库2到4,成本60
edges.emplace_back(1, 4, -50); // 仓库1到4,折扣路线,成本-50(实际是收益)
int source = 0;
vector<int> distance, parent;
bool hasNegativeCycle = bellmanFord(edges, V, source, distance, parent);
if (hasNegativeCycle) {
cout << "物流网络中存在异常折扣循环,可能导致成本无限降低!" << endl;
} else {
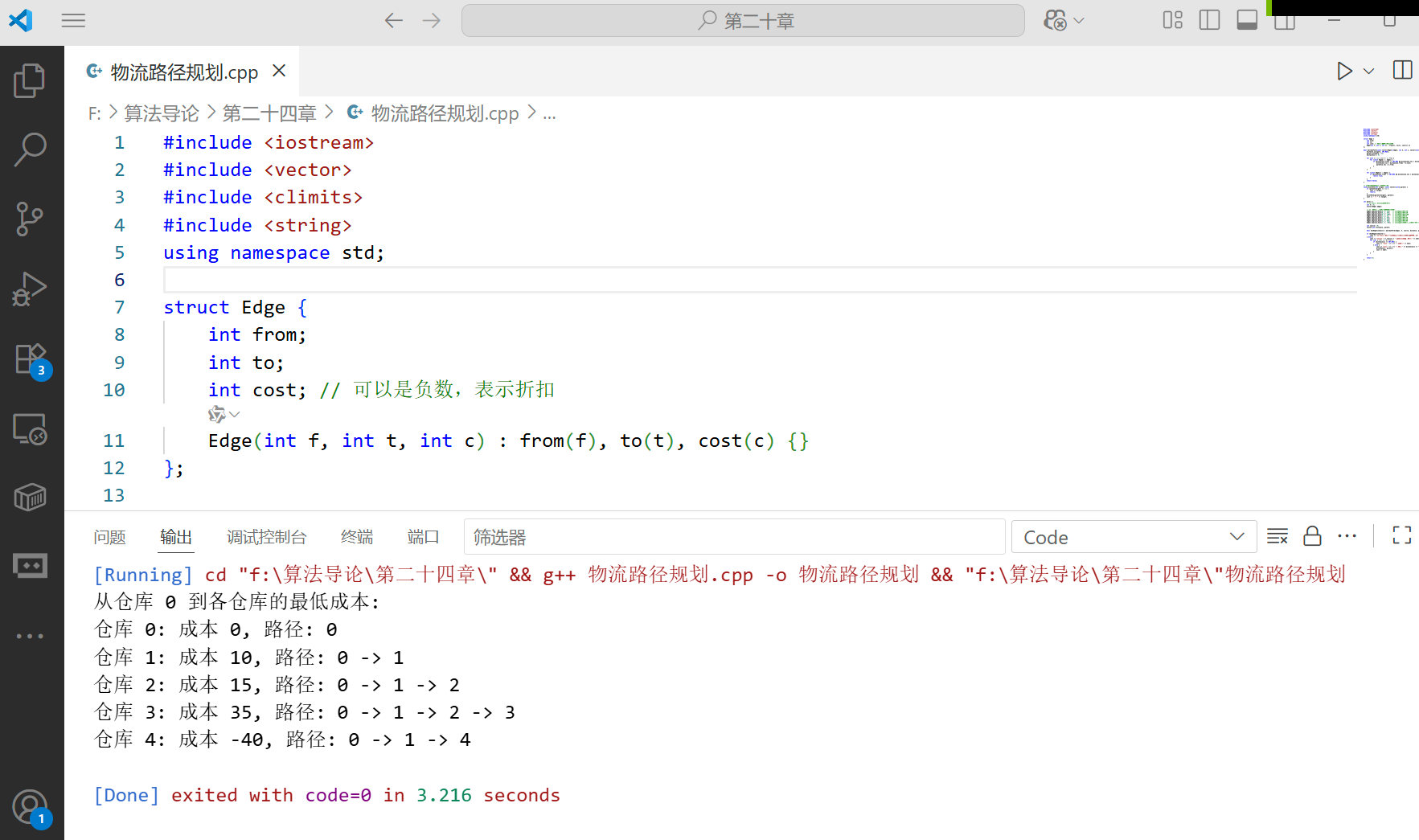
cout << "从仓库 " << source << " 到各仓库的最低成本:" << endl;
for (int i = 0; i < V; ++i) {
if (distance[i] == INT_MAX) {
cout << "仓库 " << i << ": 不可达" << endl;
} else {
cout << "仓库 " << i << ": 成本 " << distance[i] << ", 路径: ";
printPath(i, parent);
cout << endl;
}
}
}
return 0;
}
24.2 有向无环图中的单源最短路径问题
有向无环图(DAG)的单源最短路径问题可以通过拓扑排序结合松弛操作高效解决,时间复杂度为 O (V+E),优于 Bellman-Ford 算法。
算法思想
由于 DAG 中没有环,且我们按照拓扑顺序处理节点,每个节点只会被处理一次,因此算法效率很高。该算法可以处理负权边,但不能处理有环的图。
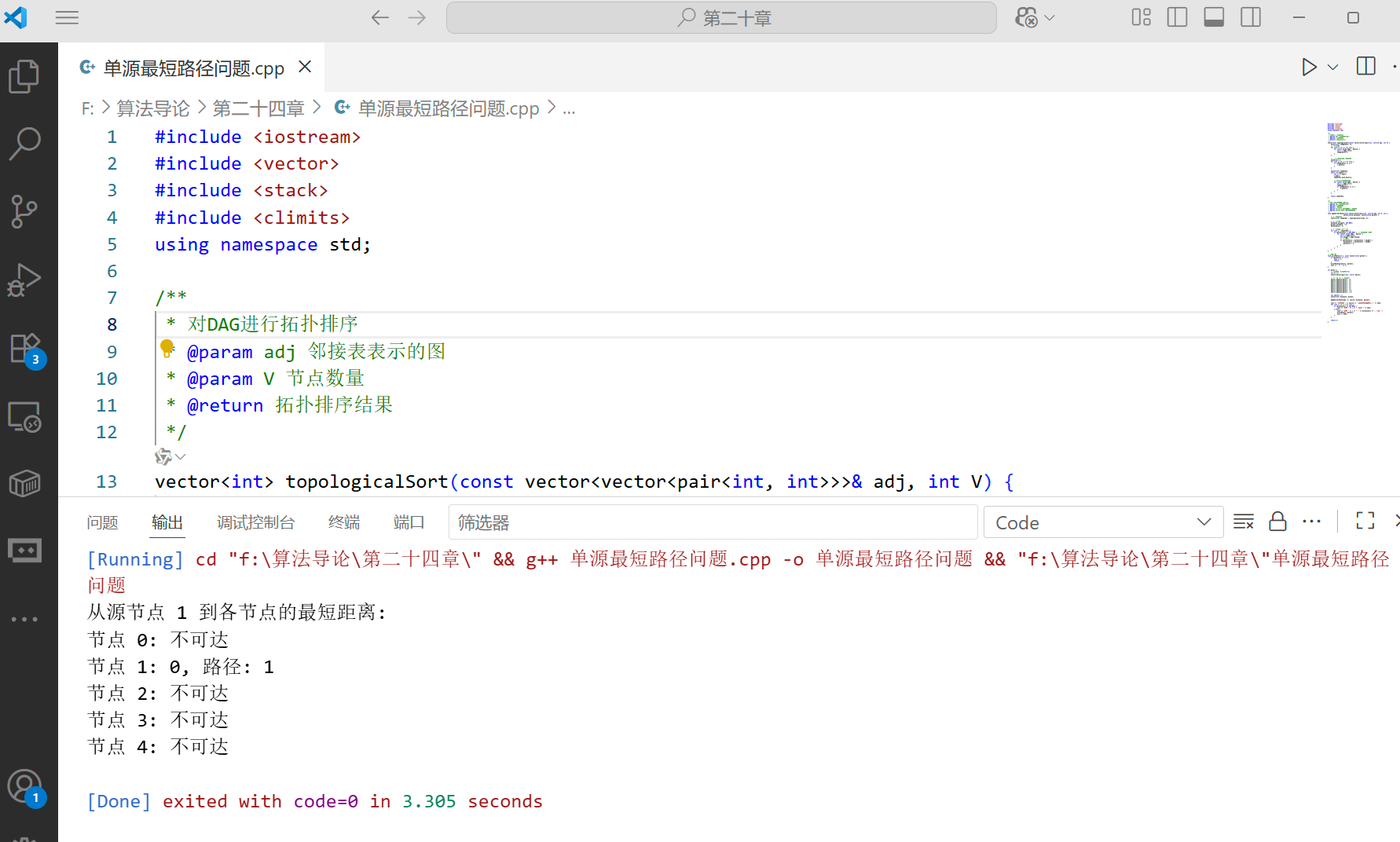
代码实现
#include <iostream>
#include <vector>
#include <stack>
#include <climits>
using namespace std;
/**
* 对DAG进行拓扑排序
* @param adj 邻接表表示的图
* @param V 节点数量
* @return 拓扑排序结果
*/
vector<int> topologicalSort(const vector<vector<pair<int, int>>>& adj, int V) {
vector<int> inDegree(V, 0);
// 计算入度
for (int u = 0; u < V; ++u) {
for (const auto& edge : adj[u]) {
int v = edge.first;
inDegree[v]++;
}
}
// 使用栈存储入度为0的节点
stack<int> s;
for (int u = 0; u < V; ++u) {
if (inDegree[u] == 0) {
s.push(u);
}
}
vector<int> topoOrder;
while (!s.empty()) {
int u = s.top();
s.pop();
topoOrder.push_back(u);
// 减少相邻节点的入度
for (const auto& edge : adj[u]) {
int v = edge.first;
inDegree[v]–;
if (inDegree[v] == 0) {
s.push(v);
}
}
}
return topoOrder;
}
/**
* DAG中的单源最短路径算法
* @param adj 邻接表表示的图
* @param V 节点数量
* @param s 源节点
* @param distance 存储最短距离的数组
* @param parent 存储前驱节点的数组
*/
void dagShortestPath(const vector<vector<pair<int, int>>>& adj, int V, int s,
vector<int>& distance, vector<int>& parent) {
// 1. 拓扑排序
vector<int> topoOrder = topologicalSort(adj, V);
// 2. 初始化
distance.assign(V, INT_MAX);
parent.assign(V, -1);
distance[s] = 0;
// 3. 按拓扑顺序松弛边
for (int u : topoOrder) {
if (distance[u] != INT_MAX) { // 仅处理可达节点
for (const auto& edge : adj[u]) {
int v = edge.first;
int weight = edge.second;
// 松弛操作
if (distance[v] > distance[u] + weight) {
distance[v] = distance[u] + weight;
parent[v] = u;
}
}
}
}
}
// 打印路径
void printPath(int v, const vector<int>& parent) {
if (parent[v] == -1) {
cout << v;
return;
}
printPath(parent[v], parent);
cout << " -> " << v;
}
int main() {
// 示例DAG: 5个节点(0-4)
int V = 5;
vector<vector<pair<int, int>>> adj(V);
// 添加边 (u, v, weight)
adj[0].emplace_back(1, 5);
adj[0].emplace_back(2, 3);
adj[1].emplace_back(2, 2);
adj[1].emplace_back(3, 6);
adj[2].emplace_back(3, 7);
adj[2].emplace_back(4, 4);
adj[2].emplace_back(1, 1);
adj[3].emplace_back(4, -1);
adj[4].emplace_back(3, -2);
int source = 1;
vector<int> distance, parent;
dagShortestPath(adj, V, source, distance, parent);
cout << "从源节点 " << source << " 到各节点的最短距离:" << endl;
for (int i = 0; i < V; ++i) {
if (distance[i] == INT_MAX) {
cout << "节点 " << i << ": 不可达" << endl;
} else {
cout << "节点 " << i << ": " << distance[i] << ", 路径: ";
printPath(i, parent);
cout << endl;
}
}
return 0;
}
综合案例及应用
下面是一个项目调度的案例,展示如何使用 DAG 最短路径算法解决关键路径问题:
#include <iostream>
#include <vector>
#include <stack>
#include <climits>
#include <algorithm>
using namespace std;
// 对DAG进行拓扑排序
vector<int> topologicalSort(const vector<vector<pair<int, int>>>& adj, int V) {
vector<int> inDegree(V, 0);
for (int u = 0; u < V; ++u) {
for (const auto& edge : adj[u]) {
int v = edge.first;
inDegree[v]++;
}
}
stack<int> s;
for (int u = 0; u < V; ++u) {
if (inDegree[u] == 0) {
s.push(u);
}
}
vector<int> topoOrder;
while (!s.empty()) {
int u = s.top();
s.pop();
topoOrder.push_back(u);
for (const auto& edge : adj[u]) {
int v = edge.first;
inDegree[v]–;
if (inDegree[v] == 0) {
s.push(v);
}
}
}
return topoOrder;
}
// 计算最长路径(关键路径)
void criticalPathAnalysis(const vector<vector<pair<int, int>>>& adj, int V,
vector<int>& earliest, vector<int>& latest, vector<int>& parent) {
vector<int> topoOrder = topologicalSort(adj, V);
// 计算最早开始时间(最长路径)
earliest.assign(V, 0);
parent.assign(V, -1);
for (int u : topoOrder) {
for (const auto& edge : adj[u]) {
int v = edge.first;
int weight = edge.second;
if (earliest[v] < earliest[u] + weight) {
earliest[v] = earliest[u] + weight;
parent[v] = u;
}
}
}
// 计算最晚开始时间
latest.assign(V, earliest.back()); // 最后一个节点的最晚时间等于最早时间
// 反转拓扑排序
reverse(topoOrder.begin(), topoOrder.end());
for (int u : topoOrder) {
for (const auto& edge : adj[u]) {
int v = edge.first;
int weight = edge.second;
if (latest[u] > latest[v] – weight) {
latest[u] = latest[v] – weight;
}
}
}
}
// 打印关键路径
void printCriticalPath(int v, const vector<int>& parent) {
if (parent[v] == -1) {
cout << v;
return;
}
printCriticalPath(parent[v], parent);
cout << " -> " << v;
}
int main() {
// 项目任务节点: 0(开始), 1-6(任务), 7(结束)
int V = 8;
vector<vector<pair<int, int>>> adj(V);
// 添加任务依赖和持续时间 (u, v, 持续时间)
adj[0].emplace_back(1, 3); // 开始 -> 任务1, 3天
adj[0].emplace_back(2, 2); // 开始 -> 任务2, 2天
adj[1].emplace_back(3, 4); // 任务1 -> 任务3, 4天
adj[1].emplace_back(4, 3); // 任务1 -> 任务4, 3天
adj[2].emplace_back(4, 2); // 任务2 -> 任务4, 2天
adj[3].emplace_back(5, 1); // 任务3 -> 任务5, 1天
adj[4].emplace_back(5, 2); // 任务4 -> 任务5, 2天
adj[4].emplace_back(6, 3); // 任务4 -> 任务6, 3天
adj[5].emplace_back(7, 3); // 任务5 -> 结束, 3天
adj[6].emplace_back(7, 2); // 任务6 -> 结束, 2天
vector<int> earliest, latest, parent;
criticalPathAnalysis(adj, V, earliest, latest, parent);
cout << "项目计划分析结果:" << endl;
cout << "项目最短完成时间: " << earliest.back() << "天" << endl;
cout << endl;
cout << "各任务时间分析:" << endl;
cout << "任务ID\\t最早开始\\t最晚开始\\t浮动时间" << endl;
for (int i = 1; i < V – 1; ++i) { // 跳过开始(0)和结束(V-1)节点
int slack = latest[i] – earliest[i];
cout << i << "\\t" << earliest[i] << "\\t\\t" << latest[i] << "\\t\\t" << slack << endl;
}
cout << endl << "关键路径(无浮动时间的任务序列): ";
printCriticalPath(V – 1, parent);
cout << endl;
return 0;
}
24.3 Dijkstra 算法
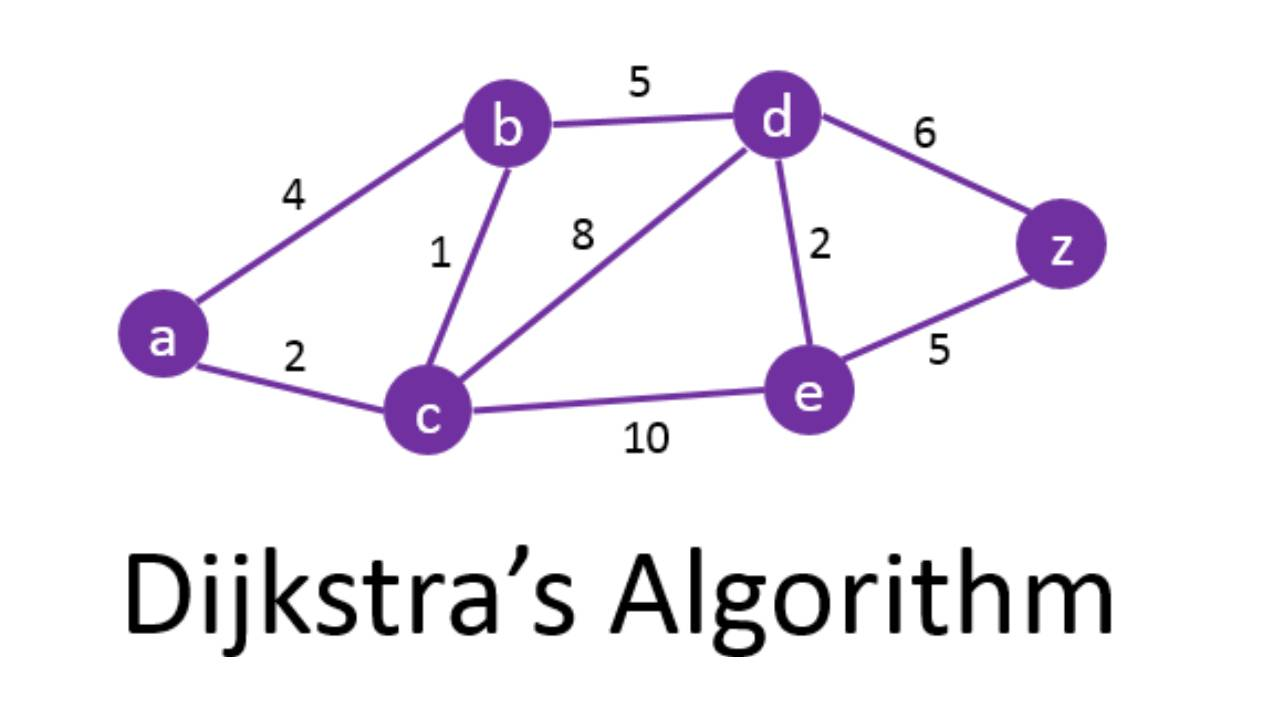
Dijkstra 算法是一种贪心算法,用于求解非负权图的单源最短路径问题。它的效率高于 Bellman-Ford 算法,尤其在使用优先队列优化后,性能表现优异。
算法思想
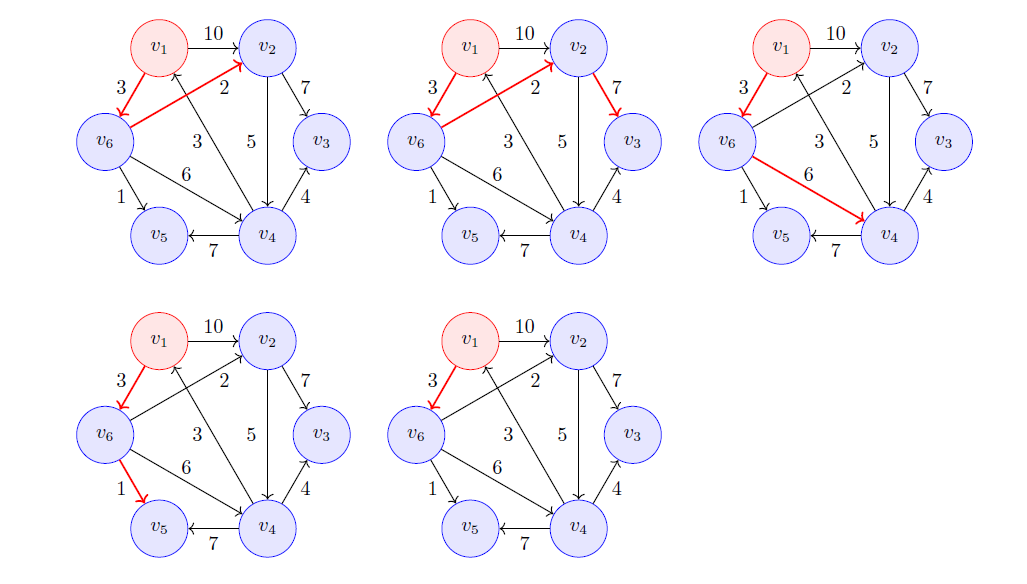
由于图中所有边的权重都是非负数,一旦某个节点被标记为已处理,我们就找到了从源节点到该节点的最短路径,无需再次考虑。
代码实现
#include <iostream>
#include <vector>
#include <queue>
#include <climits>
#include <utility>
using namespace std;
/**
* Dijkstra算法实现(使用优先队列优化)
* @param adj 邻接表表示的图
* @param V 节点数量
* @param s 源节点
* @param distance 存储最短距离的数组
* @param parent 存储前驱节点的数组
*/
void dijkstra(const vector<vector<pair<int, int>>>& adj, int V, int s,
vector<int>& distance, vector<int>& parent) {
// 初始化
distance.assign(V, INT_MAX);
parent.assign(V, -1);
distance[s] = 0;
// 优先队列: (距离, 节点), 使用最小堆
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
pq.push({0, s});
// 记录已处理的节点
vector<bool> processed(V, false);
while (!pq.empty()) {
// 提取距离最小的节点
int u = pq.top().second;
pq.pop();
// 如果已处理,跳过
if (processed[u]) continue;
processed[u] = true;
// 松弛所有出边
for (const auto& edge : adj[u]) {
int v = edge.first;
int weight = edge.second;
// 松弛操作
if (distance[v] > distance[u] + weight) {
distance[v] = distance[u] + weight;
parent[v] = u;
pq.push({distance[v], v});
}
}
}
}
// 打印路径
void printPath(int v, const vector<int>& parent) {
if (parent[v] == -1) {
cout << v;
return;
}
printPath(parent[v], parent);
cout << " -> " << v;
}
int main() {
// 示例图: 6个节点(0-5)
int V = 6;
vector<vector<pair<int, int>>> adj(V);
// 添加边 (u, v, weight)
adj[0].emplace_back(1, 7);
adj[0].emplace_back(2, 9);
adj[0].emplace_back(5, 14);
adj[1].emplace_back(0, 7);
adj[1].emplace_back(2, 10);
adj[1].emplace_back(3, 15);
adj[2].emplace_back(0, 9);
adj[2].emplace_back(1, 10);
adj[2].emplace_back(3, 11);
adj[2].emplace_back(5, 2);
adj[3].emplace_back(1, 15);
adj[3].emplace_back(2, 11);
adj[3].emplace_back(4, 6);
adj[4].emplace_back(3, 6);
adj[4].emplace_back(5, 9);
adj[5].emplace_back(0, 14);
adj[5].emplace_back(2, 2);
adj[5].emplace_back(4, 9);
int source = 0;
vector<int> distance, parent;
dijkstra(adj, V, source, distance, parent);
cout << "从源节点 " << source << " 到各节点的最短距离:" << endl;
for (int i = 0; i < V; ++i) {
if (distance[i] == INT_MAX) {
cout << "节点 " << i << ": 不可达" << endl;
} else {
cout << "节点 " << i << ": " << distance[i] << ", 路径: ";
printPath(i, parent);
cout << endl;
}
}
return 0;
}
综合案例及应用
下面是一个城市交通导航系统的案例,展示如何使用 Dijkstra 算法规划最短路径:
#include <iostream>
#include <vector>
#include <queue>
#include <climits>
#include <utility>
#include <string>
using namespace std;
// 城市节点类
class CityGraph {
private:
vector<vector<pair<int, int>>> adj; // 邻接表: (城市ID, 距离)
vector<string> cityNames; // 城市名称
public:
// 构造函数
CityGraph(int n) : adj(n) {}
// 添加城市名称
void addCityName(int id, const string& name) {
if (id >= cityNames.size()) {
cityNames.resize(id + 1);
}
cityNames[id] = name;
}
// 添加道路
void addRoad(int from, int to, int distance) {
adj[from].emplace_back(to, distance);
adj[to].emplace_back(from, distance); // 假设道路是双向的
}
// 查找最短路径
void findShortestPath(int start, int end, vector<int>& distance, vector<int>& parent) {
int V = adj.size();
distance.assign(V, INT_MAX);
parent.assign(V, -1);
distance[start] = 0;
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
pq.push({0, start});
vector<bool> processed(V, false);
while (!pq.empty()) {
int u = pq.top().second;
pq.pop();
if (u == end) break; // 提前结束,找到目标城市
if (processed[u]) continue;
processed[u] = true;
for (const auto& edge : adj[u]) {
int v = edge.first;
int dist = edge.second;
if (distance[v] > distance[u] + dist) {
distance[v] = distance[u] + dist;
parent[v] = u;
pq.push({distance[v], v});
}
}
}
}
// 打印路径
void printPath(int v, const vector<int>& parent) {
if (parent[v] == -1) {
cout << cityNames[v];
return;
}
printPath(parent[v], parent);
cout << " -> " << cityNames[v];
}
// 获取城市名称
string getCityName(int id) const {
if (id >= 0 && id < cityNames.size()) {
return cityNames[id];
}
return "未知城市";
}
};
int main() {
// 创建城市图(8个城市)
CityGraph graph(8);
// 添加城市名称
graph.addCityName(0, "北京");
graph.addCityName(1, "天津");
graph.addCityName(2, "石家庄");
graph.addCityName(3, "太原");
graph.addCityName(4, "济南");
graph.addCityName(5, "郑州");
graph.addCityName(6, "西安");
graph.addCityName(7, "武汉");
// 添加城市间道路(距离单位: 公里)
graph.addRoad(0, 1, 137); // 北京-天津
graph.addRoad(0, 2, 283); // 北京-石家庄
graph.addRoad(0, 4, 497); // 北京-济南
graph.addRoad(1, 4, 357); // 天津-济南
graph.addRoad(2, 3, 231); // 石家庄-太原
graph.addRoad(2, 5, 412); // 石家庄-郑州
graph.addRoad(3, 6, 511); // 太原-西安
graph.addRoad(4, 5, 374); // 济南-郑州
graph.addRoad(5, 6, 480); // 郑州-西安
graph.addRoad(5, 7, 536); // 郑州-武汉
graph.addRoad(6, 7, 691); // 西安-武汉
int start = 0; // 北京
int end = 7; // 武汉
vector<int> distance, parent;
graph.findShortestPath(start, end, distance, parent);
cout << "城市导航结果:" << endl;
cout << "从 " << graph.getCityName(start) << " 到 " << graph.getCityName(end)
<< " 的最短距离为: " << distance[end] << " 公里" << endl;
cout << "推荐路线: ";
graph.printPath(end, parent);
cout << endl;
return 0;
}
24.4 差分约束和最短路径
差分约束系统是一类特殊的线性规划问题,它可以转化为单源最短路径问题来求解。通过将每个约束条件转化为图中的一条边,我们可以利用最短路径算法找到满足所有约束的解。
算法思想
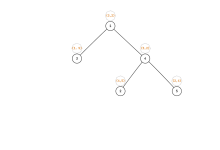
差分约束系统建模示意图
约束条件:
x1 – x0 ≤ 3
x2 – x0 ≤ 5
x3 – x1 ≤ 2
x2 – x1 ≤ 2
x3 – x2 ≤ -1
转化为图:
0 -> 1 (权重3)
0 -> 2 (权重5)
1 -> 3 (权重2)
1 -> 2 (权重2)
2 -> 3 (权重-1)
代码实现
#include <iostream>
#include <vector>
#include <climits>
using namespace std;
struct Edge {
int u, v, weight;
Edge(int u_, int v_, int w_) : u(u_), v(v_), weight(w_) {}
};
/**
* 求解差分约束系统
* @param edges 约束条件转化的边
* @param n 变量数量
* @param x 存储解的数组
* @return 是否有解
*/
bool solveDifferenceConstraints(const vector<Edge>& edges, int n, vector<int>& x) {
// 添加超级源节点0,连接到所有其他节点
vector<Edge> newEdges = edges;
for (int i = 1; i <= n; ++i) {
newEdges.emplace_back(0, i, 0);
}
// 使用Bellman-Ford算法求解
x.assign(n + 1, INT_MAX); // x[0]到x[n]
x[0] = 0;
// 松弛n次
for (int i = 0; i < n; ++i) {
for (const Edge& e : newEdges) {
if (x[e.u] != INT_MAX && x[e.v] > x[e.u] + e.weight) {
x[e.v] = x[e.u] + e.weight;
}
}
}
// 检测负权回路
for (const Edge& e : newEdges) {
if (x[e.u] != INT_MAX && x[e.v] > x[e.u] + e.weight) {
return false; // 存在负权回路,无解
}
}
return true; // 有解
}
int main() {
// 示例: 求解差分约束系统
// 变量: x1, x2, x3
// 约束:
// x1 – x2 <= 1
// x1 – x3 <= 3
// x2 – x3 <= 2
// x3 – x2 <= -1
// x2 – x1 <= -2
int n = 3; // 变量数量
vector<Edge> edges;
// 添加约束对应的边
edges.emplace_back(2, 1, 1); // x1 – x2 <= 1
edges.emplace_back(3, 1, 3); // x1 – x3 <= 3
edges.emplace_back(3, 2, 2); // x2 – x3 <= 2
edges.emplace_back(2, 3, -1); // x3 – x2 <= -1
edges.emplace_back(1, 2, -2); // x2 – x1 <= -2
vector<int> x;
bool hasSolution = solveDifferenceConstraints(edges, n, x);
if (hasSolution) {
cout << "差分约束系统的一个解为:" << endl;
for (int i = 1; i <= n; ++i) {
cout << "x" << i << " = " << x[i] << endl;
}
} else {
cout << "差分约束系统无解" << endl;
}
return 0;
}
综合案例及应用
下面是一个课程安排的案例,展示如何使用差分约束系统解决实际问题:
#include <iostream>
#include <vector>
#include <climits>
#include <string>
using namespace std;
struct Edge {
int u, v, weight;
Edge(int u_, int v_, int w_) : u(u_), v(v_), weight(w_) {}
};
bool solveCourseScheduling(const vector<Edge>& edges, int n, vector<int>& schedule) {
vector<Edge> newEdges = edges;
// 添加超级源节点0
for (int i = 1; i <= n; ++i) {
newEdges.emplace_back(0, i, 0);
}
schedule.assign(n + 1, INT_MAX);
schedule[0] = 0;
// 松弛操作
for (int i = 0; i < n; ++i) {
for (const Edge& e : newEdges) {
if (schedule[e.u] != INT_MAX && schedule[e.v] > schedule[e.u] + e.weight) {
schedule[e.v] = schedule[e.u] + e.weight;
}
}
}
// 检测负权回路
for (const Edge& e : newEdges) {
if (schedule[e.u] != INT_MAX && schedule[e.v] > schedule[e.u] + e.weight) {
return false;
}
}
return true;
}
int main() {
// 课程安排问题
// 课程: 1(算法), 2(数据结构), 3(程序设计), 4(计算机网络), 5(操作系统)
// 约束条件:
// 1. 数据结构必须在算法之后至少1周: x1 + 1 <= x2 → x2 – x1 >= 1 → x1 – x2 <= -1
// 2. 算法必须在程序设计之后: x3 <= x1 → x1 – x3 >= 0 → x3 – x1 <= 0
// 3. 计算机网络必须在数据结构之后至少2周: x2 + 2 <= x4 → x4 – x2 >= 2 → x2 – x4 <= -2
// 4. 操作系统必须在计算机网络之后: x4 <= x5 → x5 – x4 >= 0 → x4 – x5 <= 0
// 5. 操作系统必须在数据结构之后至少3周: x2 + 3 <= x5 → x5 – x2 >= 3 → x2 – x5 <= -3
// 6. 所有课程必须在10周内完成: xi <= 10 → xi – x0 <= 10 (x0=0)
int n = 5; // 5门课程
vector<Edge> edges;
vector<string> courseNames = {"", "算法", "数据结构", "程序设计", "计算机网络", "操作系统"};
// 添加约束对应的边
edges.emplace_back(2, 1, -1); // 约束1
edges.emplace_back(1, 3, 0); // 约束2
edges.emplace_back(4, 2, -2); // 约束3
edges.emplace_back(5, 4, 0); // 约束4
edges.emplace_back(5, 2, -3); // 约束5
// 所有课程必须在10周内完成
for (int i = 1; i <= n; ++i) {
edges.emplace_back(i, 0, 10); // xi – x0 <= 10
}
vector<int> schedule;
bool possible = solveCourseScheduling(edges, n, schedule);
if (possible) {
cout << "课程安排方案:" << endl;
for (int i = 1; i <= n; ++i) {
cout << courseNames[i] << " 安排在第 " << schedule[i] << " 周" << endl;
}
cout << "所有课程将在第 " << schedule[5] << " 周前完成" << endl;
} else {
cout << "无法安排这些课程,存在冲突的先修关系" << endl;
}
return 0;
}
思考题
比较不同算法:对于一个有 1000 个节点和 10000 条边的图,分别讨论在什么情况下选择 Bellman-Ford、DAG 最短路径算法或 Dijkstra 算法更合适。
负权边处理:如果图中存在负权边但不存在负权回路,Dijkstra 算法是否仍然适用?为什么?设计一个反例来说明你的结论。
算法优化:如何优化 Dijkstra 算法使其在稀疏图上的性能更好?除了优先队列,还有其他可能的优化方法吗?
差分约束扩展:如何将不等式 (x_j – x_i \\geq w) 转化为适合差分约束系统的形式?这对应图中的什么边?
最短路径树:证明最短路径树是唯一的当且仅当对于每个节点 v,从源节点 s 到 v 的最短路径是唯一的。
本章注记
单源最短路径问题是图论中的基础问题,本章介绍的算法各有其适用场景:

-
Bellman-Ford 算法:适用于存在负权边的图,能够检测负权回路,但时间复杂度较高(O (VE))。在实际应用中,其队列优化版本(SPFA 算法)更为常用。
-
DAG 最短路径算法:是处理有向无环图的高效算法(O (V+E)),可以处理负权边,特别适合任务调度、依赖分析等场景。
-
Dijkstra 算法:是处理非负权图的高效算法,使用优先队列优化后时间复杂度为 O (ElogV),广泛应用于导航系统、网络路由等领域。
-
差分约束系统:展示了图论与线性规划的深刻联系,提供了一种求解特定类型约束问题的有效方法。

最短路径算法的研究仍在继续,新的优化方法和变体不断涌现,以适应不同的应用场景和性能需求。例如,针对大规模图的分布式最短路径算法、考虑时效性的动态最短路径算法等,都是当前研究的热点方向。

理解这些算法的原理和性质,不仅有助于我们在实际问题中选择合适的方法,也为学习更复杂的图算法奠定了基础。
 网硕互联帮助中心
网硕互联帮助中心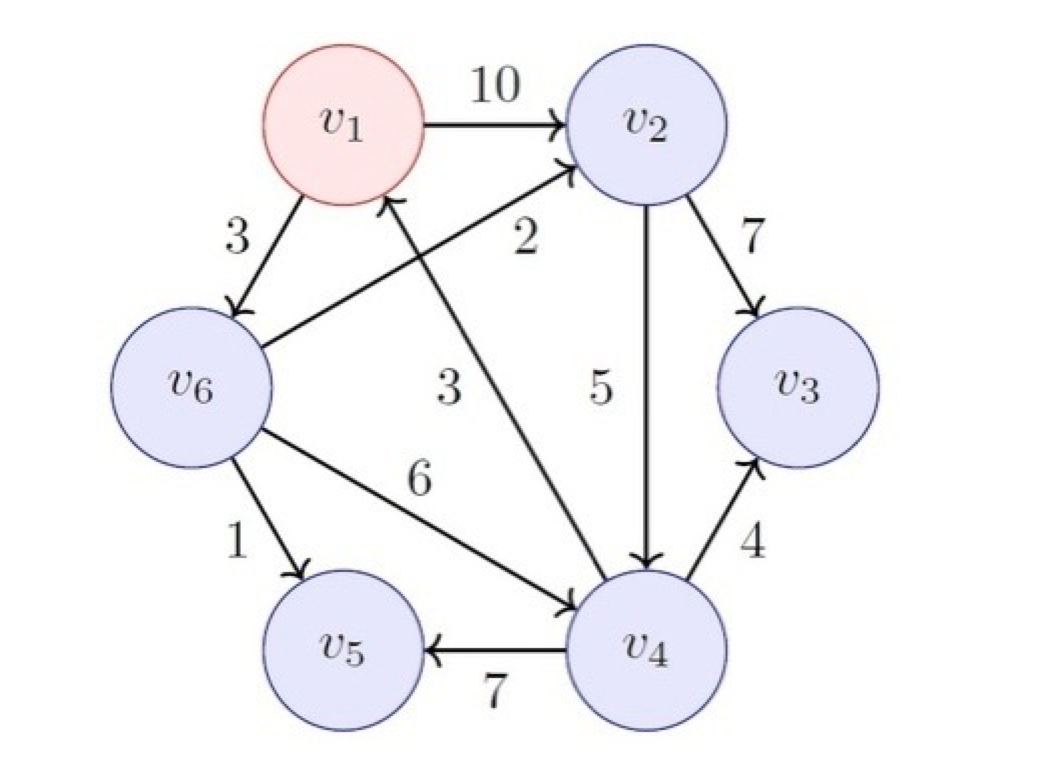



评论前必须登录!
注册