一种通用的问题解决方法 —— 分治算法（D&C算法）

        分治算法是一种通过将大规模问题分解为相互独立、结构相同的子问题进行求解的数学方法，其核心思想为“分而治之”。该方法通过递归求解子问题并合并结果，最终获得原问题的解。

        只能解决一种问题的算法毕竟用处有限，而分治算法（D&C）提供了解决问题的思路，是一个可供你选择使用的工具，让你在面对新问题时，不再束手无策。

举一个很经典的例子，现在假设你是一个农场主，你有一块1680m*640m的土地。

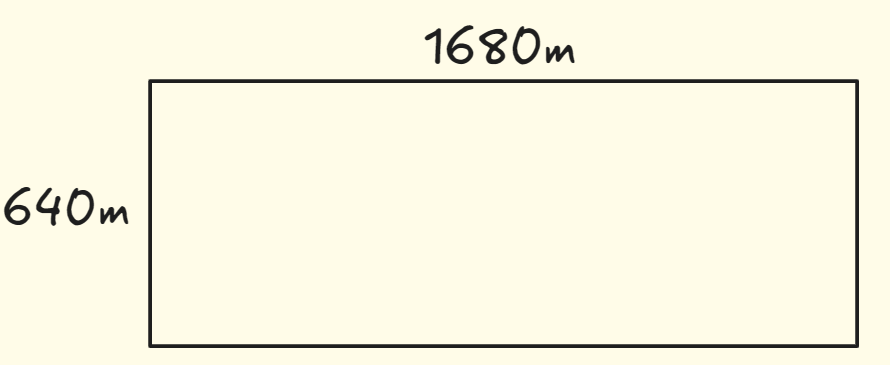
你要将这块土地均匀的分成方块，并要确保分出的方块尽可能大。下面都是错误示范。

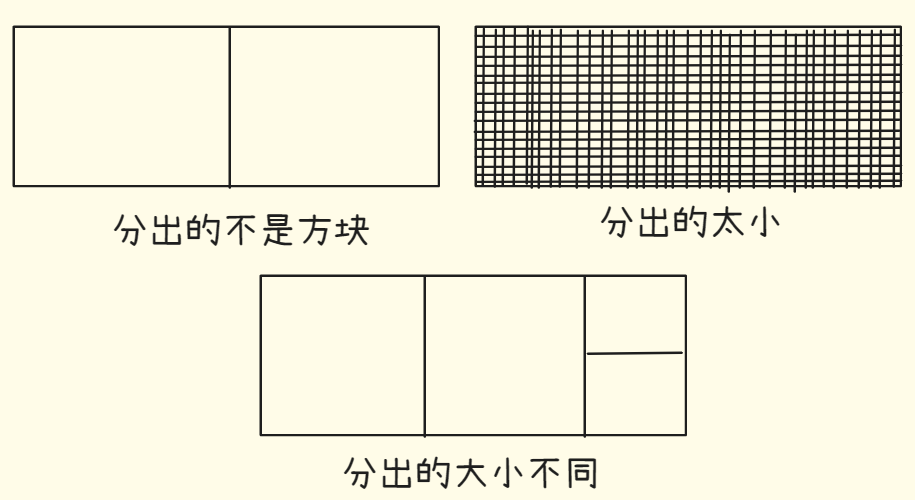
        如何将一块地均匀的分成方块，并确保分出的方块是最大的呢？使用分治算法，分治算法是递归的，所以解决问题的过程需要两个步骤：

        1. 找出基线条件，这种条件必须尽可能的简单。

        2. 能不断将问题分解或者说缩小规模，直到符合基线条件。

我们现在就来使用分治算法找出问题的解决方案。

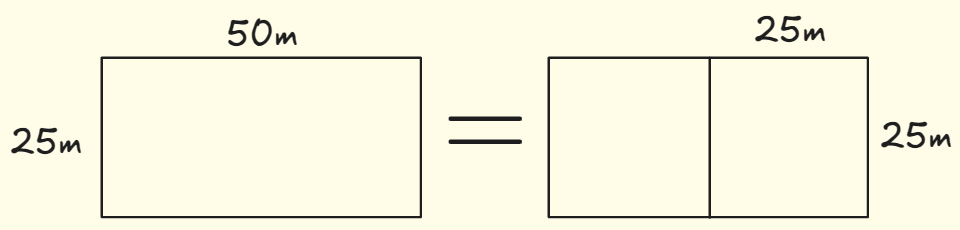
        首先，找出基线条件。就是找出最容易处理的情况，一条边的长度是另一条边的整数倍。如果一边长25m，另一边长50m，那么可使用的最大方块为25m*25m，此时你可以将这块地分成两个这样的方块。

        再找出递归条件，这才是分治算法的用武之地。根据定义，每次递归调用都必须缩小问题的规模。该怎么缩小上面问题的规模呢，我们首先可以可以找出这块地可容纳的最大方块。

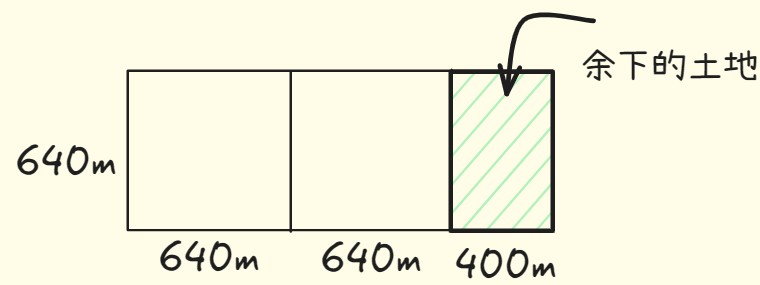
        你可以从这块地中划出两个640m*640m的方块，同时余下一小块地。那么可不可以对余下的那一小块使用相同的算法呢？现在要划分的土地更小。适用于这小块土地的最大方块，也是适用于整块土地的最大方块（不明白的可以网页搜索欧几里得算法）。你现在成功将均匀划分1680*640m的土地问题，简化缩小成了均匀划分640*400m土地的问题！

        再次使用同样算法，对剩余土地画出400*400m的方块，这将会剩下更小的土地。重复这个过程，直到余下的土地满足基线条件。

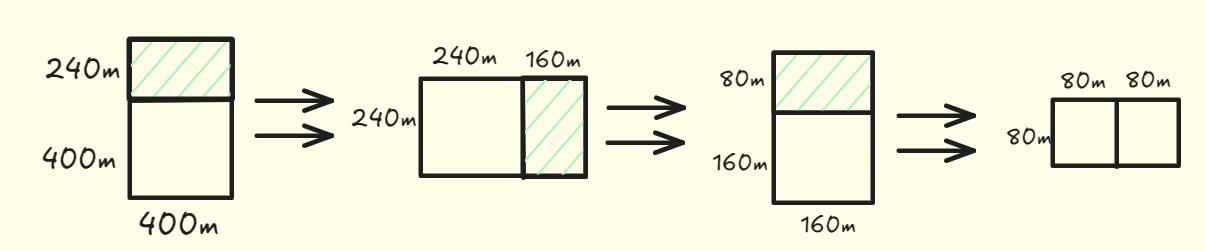
最后的土地分成两个方块后不会再余下任何土地。因此，对于最初的那片土地，适用的最大方块为80m*80m。

最后，分治算法并非可用于解决问题的算法，而是一种解决问题的思路。最常见的二分查找与快速排序就是利用了分治思想。工作原理也很简单，先找出基线条件，再思考如何缩小问题的规模向基线条件靠拢，最终解决问题。