LeetCode刷题记录----108.将有序数组转换为二叉搜索树（easy)

2025/8/7

题目（easy)：

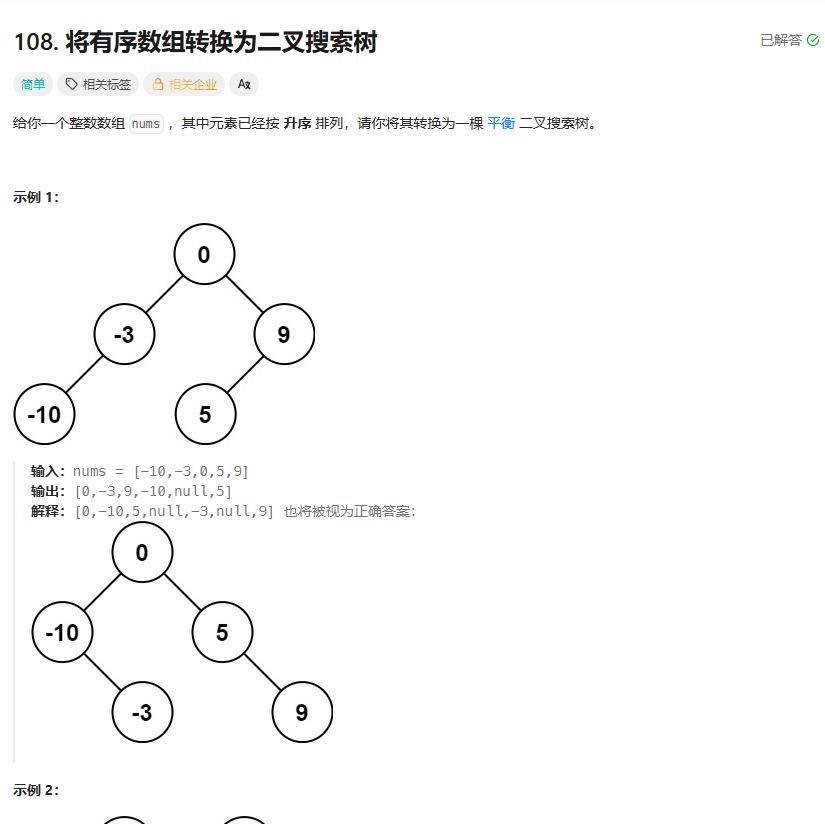
我的思路：

首先观察可以发现，建立好的二叉树它的根节点应该是这个数组的中间位置的元素值。而它的左右子树又是从中间把这个数组劈成两半之后，左右数组对应的中间位置的元素值。

大概是这么个意思（*可能稍微看起来抽象，其实也没那么抽象*）

大概步骤就是：

①从数组中间位置建立当前树的根节点（mid)，并把数组用索引值分为左右两半

②在左半数组中建立当前树的左子树（范围:[left, mid-1]）【注意要缩小区间哦，mid用过了已经】

③在右半数组中建立当前树的右子树（范围:[mid+1, right]）【注意要缩小区间哦，mid用过了已经】

④步骤三四中的左右子树由于也相当于已经知道数组，要建立平衡树，所以递归进行操作

具体代码如下：

# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]:
#二分查找
#数组中间位置作为根节点
#左右子树的根节点以它们对应的数组的中间位置作为根节点 — 递归的味道

#返回一个已经作为二叉平衡树的子树
def dfs(left:int, right:int) -> Optional[TreeNode]:
if left > right:
return None
mid = (left + right)//2
#每次缩小区间
newRoot = TreeNode(nums[mid], dfs(left, mid-1), dfs(mid+1, right))

return newRoot

#先建立头节点
left, right = 0, len(nums)-1
mid = (left + right)//2
#然后头节点的左右节点连接左右子树
head = TreeNode(nums[mid], dfs(left, mid-1), dfs(mid+1, right))

return head

时间复杂度：O（log2n）

空间复杂度：O（n)

优化思路：

其实你这个递归函数都可以根据传入的左右半个区间建立根节点的左右子树二叉搜索平衡树了，那本身完整的区间来建立二叉平衡树的对不对呀，所以完全没有必要在外面再特殊去创建根节点的，直接全部在这个递归函数中完成即可

具体代码如下：

# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]:
#二分查找
#数组中间位置作为根节点
#左右子树的根节点以它们对应的数组的中间位置作为根节点 — 递归的味道

#返回一个已经作为二叉平衡树的子树
def dfs(left:int, right:int) -> Optional[TreeNode]:
if left > right:
return None
mid = (left + right)//2
#每次缩小区间
newRoot = TreeNode(nums[mid], dfs(left, mid-1), dfs(mid+1, right))

return newRoot

#直接全部在递归函数里完成就好了
return dfs(0, len(nums)-1)

时间复杂度：O（log2n）

空间复杂度：O（n)

看了题解后发现这个数组原来是一个二叉树的中序遍历的输出结果数组。不过由这个数组没办法往回推得唯一的二叉树，也就是说其实它对应的不止有一种平衡二叉树。

而我们如果对根节点的取值做一点小小的改变的话，它也是会变成不同的平衡搜索二叉树的。我们目前根节点选的值的索引都是mid = (left + right) // 2，也就是一直选中间偏左的位置元素作为根节点的值。

那当然，我们也可以有

mid = (left + right + 1) // 2        【一直选中间偏右位置的元素作为根节点的值】

mid = (left + right + randint(0,1))//2        【随机选中间偏左或偏右的元素作为根节点的值】

只有这里不一样，其他代码都一样，所以就不特意复制粘贴过来了。

总结：

①还是老毛病，不要边想边做，思考要慢，解题才能快。不然其实是变相的偷懒

②对于进行递归操作，我们要首先明确想好我们希望输入什么，并从递归函数中得到什么。比如这里的递归我们需要得到建立好的平衡树的根节点，而要得到这个根节点需要的值我们就需要知道这个数组的区间范围，才能去取得中间的值，所以我们就知道输入是要建立平衡二叉搜索树的数组的区间。

③对于二分搜索，一定要记得每次搜索完中间的值之后，再去搜索左右两半区间的时候要把之前的中间值排除出去，不然一直会有重复的隐患的。这很不好

④每个树都有唯一确定的中序遍历输出顺序，但是同一个中序遍历输出顺序可以对应多个树