【微实验】妈妈我的MATLAB会识别声音的基频了！

 前情提要：

【超详细】科普：别再只会用自相关！YIN 和 PYIN 如何破解音频隐藏密码？-CSDN博客

今天用MATLAB实现YIN算法——

 它是一种经典的基频（F0）提取算法，通过计算信号的自相关函数及其累积均值归一化，来定位基频周期，适用于语音、乐器等信号的基频检测，具有较好的抗噪声性能。先来看YIN，这里，笔者在Cubase中导出了管子吹奏单音的音频文件。

废话不说，代码如下：

clear; clc; close all;
[audio, Fs] = audioread('管子.wav'); % 替换为你的音频文件
audio = audio(:,1); % 取单声道
t_total = (0:length(audio)-1)/Fs; % 总时间轴

% 选取一段语音帧（避免静音，取中间有效部分）
frame_len = 2048; % 帧长（建议取采样率的1/10~1/5，如16kHz对应2048）
start_idx = round(0.3*length(audio)); % 起始索引
x = audio(start_idx:start_idx+frame_len-1); % 截取一帧信号
t_frame = (0:frame_len-1)/Fs; % 该帧时间轴

% 可视化1：原始音频帧波形
figure('Name','步骤1：原始音频帧');
plot(t_frame, x, 'LineWidth',1.2);
xlabel('时间 (s)'); ylabel('振幅');
title('待分析的音频帧波形'); grid on;

% 步骤2：计算差分函数d(tao)
max_lag = floor(frame_len/2); % 最大滞后tao（不超过帧长一半）
d = zeros(1, max_lag); % 差分函数结果

for tao = 1:max_lag
% 差分函数：d(tao) = sum_{n=0}^{N-tao-1} (x(n) – x(n+tao))^2
d(tao) = sum( (x(1:end-tao) – x(1+tao:end)).^2 );
end

% 可视化2：差分函数曲线
tao_axis = 1:max_lag; % 滞后tao轴
figure('Name','步骤2：差分函数d(tao)');
plot(tao_axis, d, 'b', 'LineWidth',1.2);
xlabel('滞后tao (采样点)'); ylabel('d(tao)');
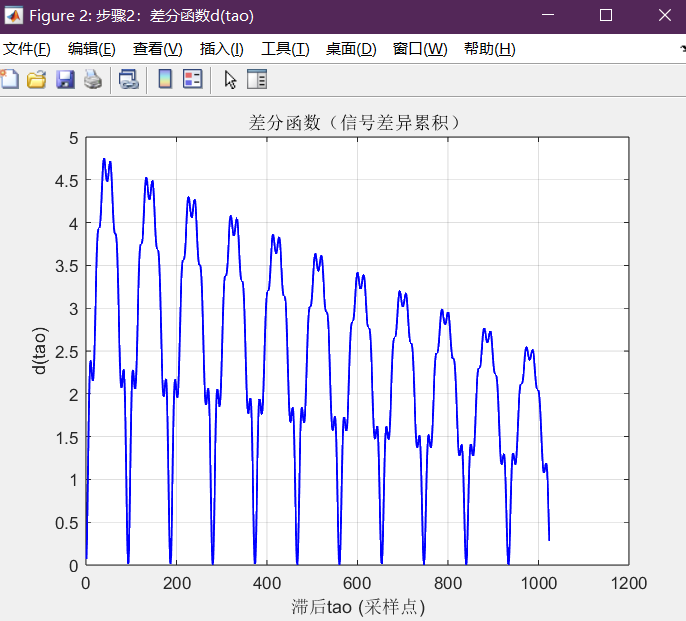
title('差分函数（信号差异累积）'); grid on;

% 步骤3：计算累积平均归一化差分函数（CMNDF）
cmndf = zeros(1, max_lag);
cmndf(1) = 1; % tao=0处定义为1（避免除以0）

for tao = 2:max_lag
% 归一化：cmndf(tao) = d(tao) / ( (1/tao) * sum_{j=1}^tao d(j) )
cmndf(tao) = d(tao) / ( (1/tao) * sum(d(1:tao)) );
end

% 可视化3：CMNDF曲线
figure('Name','步骤3：累积平均归一化差分函数（CMNDF）');
plot(tao_axis, cmndf, 'r', 'LineWidth',1.2);
xlabel('滞后tao (采样点)'); ylabel('CMNDF(tao)');
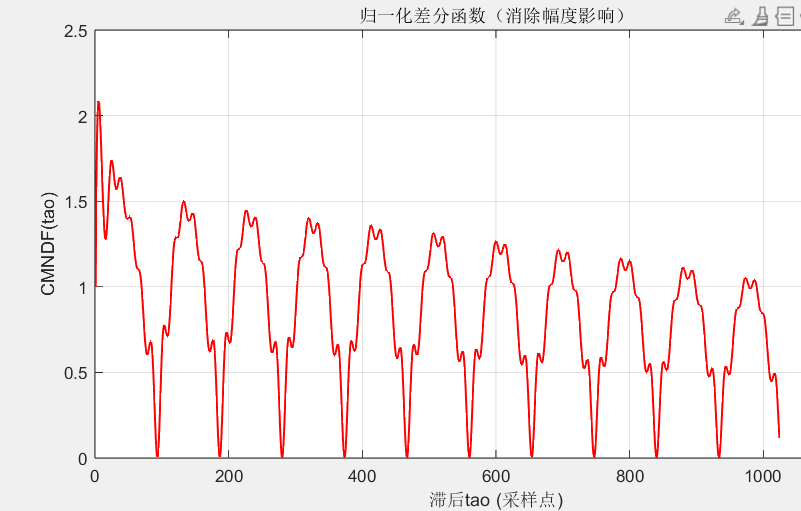
title('归一化差分函数（消除幅度影响）'); grid on;

% 步骤4：阈值检测与基频周期定位
threshold = 0.1; % 阈值（通常取0.1~0.2，可根据信号调整）
valid_tao = find(cmndf < threshold); % 找到所有小于阈值的tao

if isempty(valid_tao)
% 若无有效tao，取最小CMNDF对应的tao
[~, min_idx] = min(cmndf);
f0_period = min_idx;
else
% 取第一个小于阈值的tao作为基频周期
f0_period = valid_tao(1);
end

% 可视化4：标记基频周期在CMNDF上的位置
figure('Name','步骤4：基频周期检测结果');
plot(tao_axis, cmndf, 'r', 'LineWidth',1.2);
hold on;
plot(f0_period, cmndf(f0_period), 'ko', 'MarkerSize',8, 'MarkerFaceColor','g');
line([0 max_lag], [threshold threshold], 'Color','k', 'Linestyle','–');
text(max_lag*0.7, threshold+0.05, ['阈值 = ', num2str(threshold)], 'Color','k');
xlabel('滞后tao (采样点)'); ylabel('CMNDF(tao)');
title(['基频周期定位：tao = ', num2str(f0_period), ' 采样点']);
grid on; hold off;

% 步骤5：计算基频并可视化结果
f0 = Fs / f0_period; % 基频 = 采样率 / 周期（Hz）

% 可视化5：原始信号与基频标注
figure('Name','最终结果：基频值');
plot(t_frame, x, 'LineWidth',1.2);
xlabel('时间 (s)'); ylabel('振幅');
title(['基频检测结果：', num2str(round(f0,1)), ' Hz']);
text(t_frame(end)*0.7, max(x)*0.8, ['F0 = ', num2str(round(f0,1)), ' Hz'], …
'BackgroundColor','y', 'FontWeight','bold');
grid on;

% 输出结果
disp(['检测到的基频：', num2str(round(f0,1)), ' Hz']);
disp(['对应的周期：', num2str(f0_period), ' 采样点（', num2str(f0_period/Fs*1000,2), ' ms）']);

代码效果展示：

这是原始波形——

管子吹奏音色的波形

差分函数这里，对应着“做减法”，因为这一段音频的基频是一致的，因此差分函数每个峰和谷的形状非常类似，只是高低不同。

归一化，消除幅度的影响，同事让零点处不再是谷值

设定阈值0.1，提取第一个谷值。

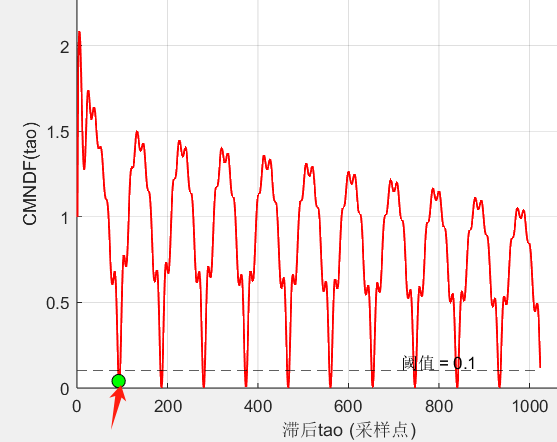
得到检测结果：