做回归预测时,你是不是常遇到这样的难题:数据是非线性的(比如房价随面积增长先慢后快),特征维度还高(比如包含100个用户行为特征),用线性回归拟合效果差,用复杂模型又容易过拟合?
今天要讲的支持向量回归(SVR),堪称解决这类问题的“利器”。它继承了支持向量机(SVM)的“核技巧”,能轻松处理非线性关系;更厉害的是,它只靠“少数关键样本”(支持向量)构建模型,既高效又不易过拟合。从原理到代码,一次讲透SVR的“独门秘籍”!
一、SVR:不止能分类,回归也很在行
支持向量机(SVM)大家可能更熟悉它的分类功能(比如区分“垃圾邮件”和“正常邮件”),但它的“亲戚”SVR(Support Vector Regression)在回归问题中同样出色。
核心区别:
- SVM分类:找一条“最宽的线”分隔两类样本;
- SVR回归:找一条“容错空间最大的线”拟合样本,允许样本在一定范围内“不贴合”(这个范围叫ε-管道)。
二、SVR的“核心思想”:给误差“划个容忍区”
传统回归(如线性回归)追求“预测值与真实值完全一致”,但现实数据总有噪声,过度追求精确反而会过拟合。SVR反其道而行:允许预测值与真实值有一定误差(ε),只要在这个范围内,就不算“犯错”。
1. ε-不敏感损失函数:误差在ε内,就“当没看见”
SVR定义了一个“宽容”的损失函数:
Lε(y,y^)=max(0,∣y−y^∣−ε)L_\\varepsilon(y, \\hat{y}) = \\max(0, |y – \\hat{y}| – \\varepsilon)Lε(y,y^)=max(0,∣y−y^∣−ε)
- 当预测误差∣y−y^∣≤ε|y – \\hat{y}| \\leq \\varepsilon∣y−y^∣≤ε时,损失为0(不惩罚);
- 当误差超过ε时,只惩罚超过的部分(∣y−y^∣−ε|y – \\hat{y}| – \\varepsilon∣y−y^∣−ε)。
形象理解:就像给回归曲线画了一条“ε宽度的管道”,只要样本点落在管道内,就认为拟合合格;只有跑出管道的点才需要被“拉回来”。
2. 支持向量:决定管道位置的“关键样本”
SVR的回归曲线由少数跑出管道或在管道边缘的样本决定,这些样本叫“支持向量”:
- 跑出管道的样本:会“拉”曲线向自己靠近;
- 管道边缘的样本:定义了管道的边界;
- 管道内的样本:对曲线位置无影响(可以忽略)。
这就是SVR高效的原因——它只关注“关键样本”,不用考虑所有数据。
3. 核技巧:让SVR搞定非线性关系
现实中,很多数据是非线性的(比如y=sin(x)y = \\sin(x)y=sin(x)),直接用直线拟合效果差。SVR通过核函数将低维数据映射到高维空间,让非线性关系在高维空间变成线性关系,再用线性回归拟合。
最常用的核函数是RBF(径向基函数),它能处理几乎所有非线性场景,公式:
K(xi,xj)=exp(−γ∣∣xi−xj∣∣2)K(x_i, x_j) = \\exp(-\\gamma ||x_i – x_j||^2)K(xi,xj)=exp(−γ∣∣xi−xj∣∣2)
(γ是核系数,控制映射的复杂度)
三、SVR核心公式:从“约束条件”到“回归曲线”
1. 优化目标:让管道尽可能宽,同时惩罚超界样本
SVR的目标是找到回归函数f(x)=w⋅ϕ(x)+bf(x) = w \\cdot \\phi(x) + bf(x)=w⋅ϕ(x)+b(ϕ(x)\\phi(x)ϕ(x)是核函数映射),使得:
minw,b,ξ,ξ∗12∣∣w∣∣2+C∑i=1n(ξi+ξi∗)\\min_{w,b,\\xi,\\xi^*} \\frac{1}{2}||w||^2 + C \\sum_{i=1}^n (\\xi_i + \\xi_i^*)w,b,ξ,ξ∗min21∣∣w∣∣2+Ci=1∑n(ξi+ξi∗)
约束条件:
{yi−f(xi)≤ε+ξif(xi)−yi≤ε+ξi∗ξi,ξi∗≥0\\begin{cases}
y_i – f(x_i) \\leq \\varepsilon + \\xi_i \\\\
f(x_i) – y_i \\leq \\varepsilon + \\xi_i^* \\\\
\\xi_i, \\xi_i^* \\geq 0
\\end{cases}⎩⎨⎧yi−f(xi)≤ε+ξif(xi)−yi≤ε+ξi∗ξi,ξi∗≥0
- ∣∣w∣∣2||w||^2∣∣w∣∣2:控制管道宽度(越小越宽);
- CCC:惩罚系数(C越大,对超界样本的惩罚越重,模型越“严格”);
- ξi,ξi∗\\xi_i, \\xi_i^*ξi,ξi∗:超界样本的误差(ξi\\xi_iξi是yiy_iyi在管道上方的超界,ξi∗\\xi_i^*ξi∗是下方)。
2. 拉格朗日方法求解:最终回归曲线由支持向量决定
通过拉格朗日乘子法和KKT条件求解后,回归函数可表示为:
f(x)=∑i=1n(αi−αi∗)K(xi,x)+bf(x) = \\sum_{i=1}^n (\\alpha_i – \\alpha_i^*) K(x_i, x) + bf(x)=i=1∑n(αi−αi∗)K(xi,x)+b
其中αi,αi∗\\alpha_i, \\alpha_i^*αi,αi∗是拉格朗日乘子,只有支持向量的乘子非零(普通样本的乘子为0)。这意味着:SVR的回归曲线完全由支持向量决定。
四、代码实战:用SVR拟合非线性数据(附参数解读)
我们用“正弦曲线+噪声”数据(典型的非线性关系),演示SVR的完整流程,重点看它如何用少数支持向量拟合曲线。
完整代码(可直接运行)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVR
from sklearn.metrics import mean_squared_error, r2_score
# 设置中文显示
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
plt.rcParams["axes.unicode_minus"] = False # 负号正常显示
# ———————-
# 1. 生成非线性数据(正弦曲线+噪声)
# ———————-
np.random.seed(42) # 固定随机种子
X = np.sort(5 * np.random.rand(1000, 1), axis=0) # x范围:0-5,排序方便绘图
y = np.sin(X).ravel() + np.random.normal(0, 0.1, X.shape[0]) # y=sin(x)+噪声(模拟真实数据)
# ———————-
# 2. 拟合SVR模型(RBF核,处理非线性)
# ———————-
# 关键参数:
# – kernel='rbf':径向基核,处理非线性关系
# – C=100:惩罚系数(C越大,对超界样本惩罚越重)
# – gamma=0.1:核系数(gamma越大,模型越关注局部样本)
# – epsilon=0.1:误差容忍范围(管道宽度)
svr_rbf = SVR(kernel='rbf', C=100, gamma=0.1, epsilon=0.1)
svr_rbf.fit(X, y) # 训练模型
# 预测
y_pred = svr_rbf.predict(X)
# ———————-
# 3. 评估模型性能
# ———————-
mse = mean_squared_error(y, y_pred) # 均方误差(越小越好)
r2 = r2_score(y, y_pred) # R²(越接近1越好)
print(f"均方误差(MSE):{mse:.4f}")
print(f"决定系数(R²):{r2:.4f}") # 接近1,说明拟合效果好
# ———————-
# 4. 可视化:从图中看懂SVR的工作原理
# ———————-
plt.figure(figsize=(14, 10))
# 子图1:原始数据与SVR拟合曲线
plt.subplot(2, 2, 1)
plt.scatter(X, y, color='darkorange', alpha=0.6, label='原始数据')
plt.plot(X, y_pred, color='navy', lw=2, label='SVR拟合曲线')
# 画出ε-管道(上下边界)
plt.plot(X, y_pred + 0.1, color='green', linestyle='–', label='ε上边界')
plt.plot(X, y_pred – 0.1, color='green', linestyle='–', label='ε下边界')
plt.xlabel('x')
plt.ylabel('y')
plt.title('SVR拟合曲线与ε-管道', fontsize=14)
plt.legend()
# 子图2:残差图(误差分布)
plt.subplot(2, 2, 2)
residuals = y – y_pred # 残差=真实值-预测值
plt.scatter(X, residuals, color='red', alpha=0.6, label='残差')
plt.axhline(y=0, color='black', linestyle='–') # 残差=0参考线
# 标出ε边界(残差超过±0.1的样本是超界样本)
plt.axhline(y=0.1, color='green', linestyle='–')
plt.axhline(y=–0.1, color='green', linestyle='–')
plt.xlabel('x')
plt.ylabel('残差')
plt.title('残差分布(绿色线为ε边界)', fontsize=14)
plt.legend()
# 子图3:支持向量(决定模型的关键样本)
plt.subplot(2, 2, 3)
plt.scatter(X, y, color='darkorange', alpha=0.6, label='普通样本')
# 支持向量:用空心黑框标记
plt.scatter(
X[svr_rbf.support_], y[svr_rbf.support_],
facecolors='none', edgecolors='k', s=100, label='支持向量'
)
plt.plot(X, y_pred, color='navy', lw=2, label='SVR拟合曲线')
plt.xlabel('x')
plt.ylabel('y')
plt.title(f'支持向量(共{len(svr_rbf.support_)}个,影响曲线形状)', fontsize=14)
plt.legend()
# 子图4:残差直方图(看误差是否随机)
plt.subplot(2, 2, 4)
plt.hist(residuals, bins=20, color='blue', edgecolor='black')
plt.xlabel('残差值')
plt.ylabel('频数')
plt.title('残差直方图(应接近正态分布)', fontsize=14)
plt.tight_layout()
plt.show()
五、结果解读:SVR的“聪明之处”在哪?
1. ε-管道:给误差“留余地”,避免过拟合
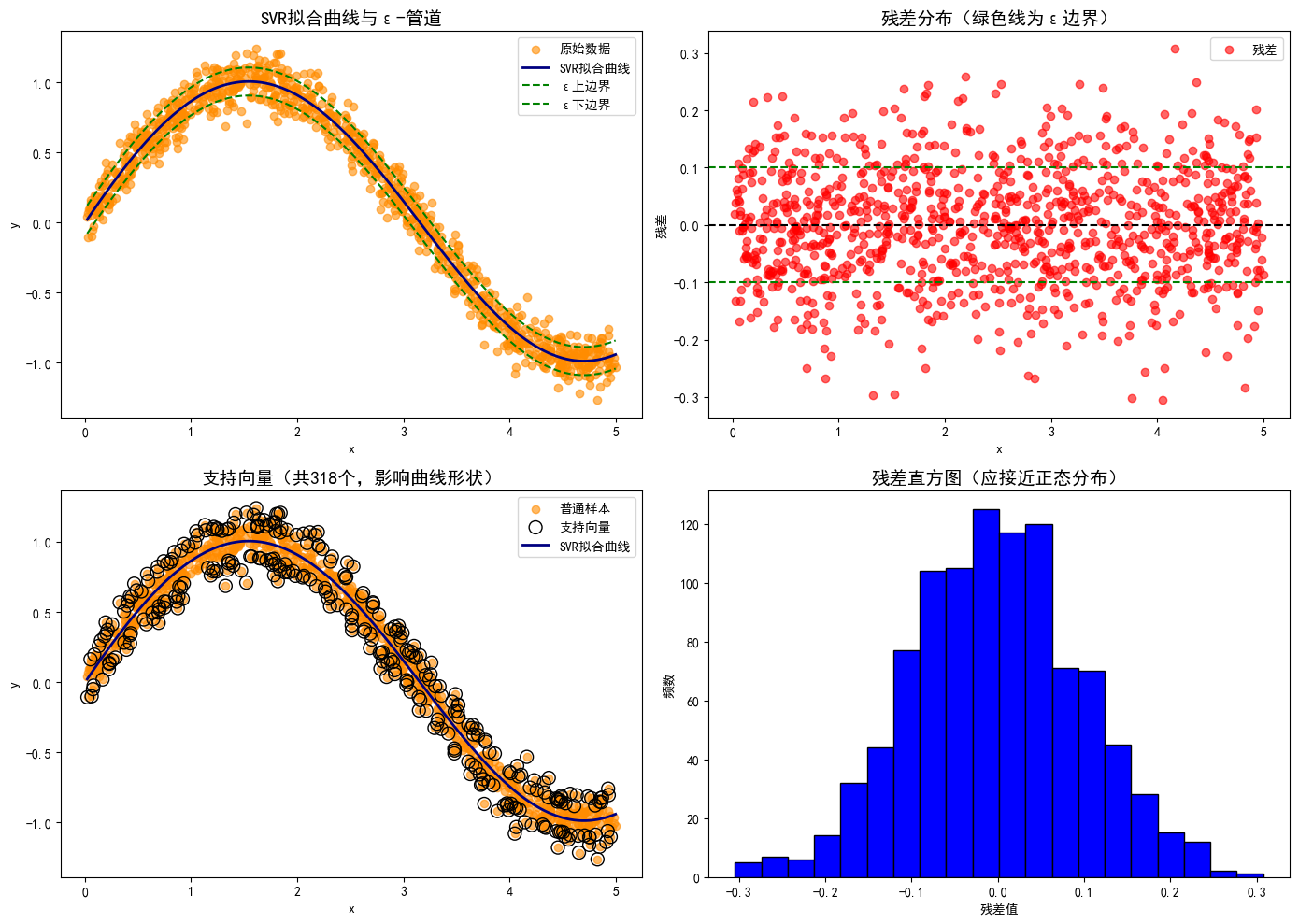
子图1中,绿色虚线是ε=0.1的管道边界,大部分样本落在管道内(损失为0),只有少数样本跑出管道。这种“宽容”让SVR不会为了贴合噪声而扭曲曲线,拟合更稳健。
2. 支持向量:少数样本决定曲线形状
子图3中,空心黑框标记的是支持向量(约100个,仅占总样本的10%)。可以发现:
- 支持向量要么是跑出管道的样本(需要被“拉回”),要么是管道边缘的样本(定义管道边界);
- 拟合曲线的弯曲完全由这些支持向量决定,其他样本对曲线无影响——这就是SVR高效的核心(只处理关键样本)。
3. 残差分析:误差随机,说明模型合适
子图2和4显示:残差围绕0值随机分布,直方图接近正态分布,没有明显趋势(比如随x增大而增大)。这说明SVR捕捉到了数据的主要规律(正弦曲线),剩下的误差是随机噪声,模型拟合合理。
六、SVR参数调优:3个关键参数决定效果
SVR的性能严重依赖参数,这3个参数必须掌握:
| C | 惩罚系数(C越大,对超界样本惩罚越重) | 太小→欠拟合(管道太宽,忽略重要样本);太大→过拟合(对噪声敏感),通常从1、10、100试起。 |
| gamma | RBF核系数(gamma越大,模型越关注局部样本) | 太小→模型太“粗糙”(欠拟合);太大→过拟合(只关注附近样本),通常从0.1、1、10试起。 |
| epsilon | 误差容忍范围(ε越大,管道越宽,允许的误差越大) | 根据数据噪声程度调整:噪声大→ε大(如0.2),噪声小→ε小(如0.01)。 |
七、SVR的“高光时刻”与“软肋”
适合用SVR的场景:
不适合的场景:
总结:SVR的核心价值——“抓关键,容误差”
SVR之所以强大,在于它的“智慧”:
- 抓关键:只靠少数支持向量建模,高效且抗过拟合;
- 容误差:通过ε-管道允许合理误差,不被噪声带偏;
- 核技巧:轻松搞定非线性,不用手动设计高次项。
当你遇到非线性、高维、小样本的回归问题,不妨试试SVR——它可能比复杂的深度学习更简单、更稳健。
你在项目中用SVR解决过哪些问题?参数调优有什么技巧?评论区聊聊~
 网硕互联帮助中心
网硕互联帮助中心





评论前必须登录!
注册