普通+可撤销+扩展域并查集详解【数据结构】

简介

不要问我为什么没有带权并查集

并查集是一种极其常用的数据结构（英文名DSU）。它的主要工作范围是处理结点的合并以及查询操作，当然并查集也可以用于支持Kruskal最小生成树的运行以及实现各种阴间功能。

并查集有一种极其阴暗甚至变态的理解方式，本文将围绕次理解展开。

（万恶之源）普通并查集

基础操作

这是最基础的并查集。我们可以假设有5个结点。我们也可以把它们想象成人，这里我们把一个人的爹看成它的父节点。

现在给你一种操作，即合并两个结点所在的联通块。用人话说，我们把这两个人的家族融合成一个。我们该如何进行这样的操作呢？很简单，我们让一家的祖先当另一家的儿子，这样两家就会变成新的家族（请勿模仿）。我们找祖先只需维护每个人的爹，一直往上查就行。

我们假设我们合并第一个人和第三个人的家族。

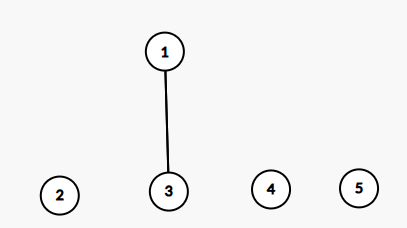
再次合并1的家族以及5的家族。

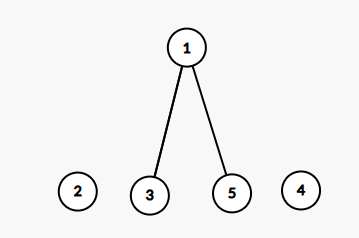
5个人问一问父亲就知道谁和谁是一家的，但如果我们有几千几万个人呢？那不是年都过完了才知道给谁送红包吗？这也很简单，我们找到比对的两个人看一眼他们的祖先相不相同就行了。

比如我们想知道2和3是不是一家的，我们知道2是孤家寡人，3的祖先是1，他们祖先不一样，所以不是一家的。

如果你闲的发慌，想知道有几个家族，这也很好办，毕竟每次合并如果祖先不同家族数量必定减1，而起初所有人都是孤家寡人，我们简单维护就行。

逐渐离谱（启发式合并）

我们发现查祖宗成为确认和合并最大的阻碍，我们观察上图的家族树，似乎人多的家族查起来会慢不少。如果有一个人少的家族，比如2，与1的家族合并，我们如果随机挑选父亲有可能会使3和5的查询过程更加艰难，而如果2认1做爹就不会有这种问题。

这就是启发式合并的原理，谁家人多谁做爹。

彻底阴间（路径压缩）

人们发现，即使是这样查祖宗的效率依旧不高，我们需要更高效一些，于是最阴间的操作出现了。当一个人询问父亲他的父亲，以及他父亲的父亲是谁时，我们可以将他们的父亲顺便改成祖宗。

比如图中的1还有一个祖先6，这时3想知道他祖先是谁，于是往上询问。历经千辛万苦他得到了祖宗的信息，可如果不记录下来下次还得再来一次。3觉得自己遭不住了，干脆直接让祖宗当自己的爹，这样中间的一长串人就省下来了。

                ​​​​​​​        ​​​​​​​        

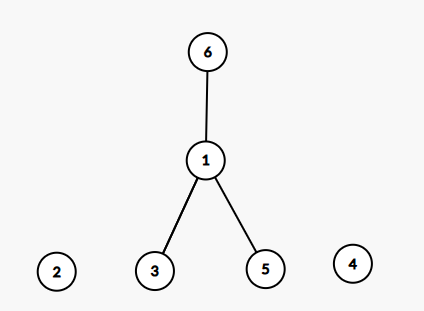
当然还有另一种优化按秩合并（谁辈数多谁家祖先当爹），但是出题入变态到卡启发式合并是不太可能的。

（假如人们可以后悔）可撤销并查集

可撤销并查集比起普通并查集只多了一个操作，即撤销上一个操作。这就好比吕布一开始拜丁原为义父，但又收到挑拨（省略一个人头），撤销了这个操作，转而拜董卓为义父（省略一个烤全猪）。那么此时我们应该如何维护并查集呢？

这其实很简单。我们维护一个栈，记录每次要合并家族的两个人的祖宗（人多的在前，人少的在后），在需要时我们将其弹出。在此之前，使用可撤销并查集需要注意：千万不能使用路径压缩！！！为什么？因为路径压缩会直接改变原本父亲序列的样子，导致我们还原时会出现偏差。

如何还原？我们获取栈顶的两个元素，我们把后面的元素，也就是认贼作父的那家的祖宗的父亲数组改回自己，并把人多那家的人数减去自己家的人数，这样人们就可以效仿吕布了。

（家族之间的战争）扩展域并查集

扩展域并查集大概是运用最广的并查集模板了。大家应该都听说过那道臭名昭著经典的题目——食物链。我们不讨论这种复杂的情况，我们考虑一种简化版本。已知这个社会中有两种关系，一种是交战，一种是结盟。原本这很好维护，但通过生活常识我们知道交战方的交战方就是自己的盟友（敌人的敌人就是朋友）。如此以来我们要维护的就多了。

当我们找到两个交战的家族时，我们可以把并查集开成两倍空间，另一倍空间存储这个家族的敌人。当又出现敌对家族时，我们可以把第二倍空间的那个家族与这个家族合并。例如2的家族正在和1的家族交战，那么对于2来说，他的家族的敌对家族就是1的家族，此时如果4的家族也来进攻2，我们就可以合并1的家族和4的家族，合并方式随意。

这样我们就可以精准的求出两个人之间是敌是友，有效避免了友伤拉满。

代码以及例题

可能有一些模版是没有例题的，比如可撤销并查集，因为它主要用于线段树分治，我也不会写。

基础并查集

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e5+10;
int n,m,f[N],op,x,y,siz[N];
int fa(int x){
if(f[x]==x) return x;
else return f[x]=fa(f[x]);
}
int read(){
char c;int x=0,f=1;
while(c<'0'||c>'9'){c=getchar();if(c=='-') f=-1;}
while(c>='0'&&c<='9') x=x*10+c-'0',c=getchar();
return x*f;
}
signed main(){
n=read(),m=read();
for(int i=1;i<=n;i++) f[i]=i, siz[i]=1;
while(m–){
op=read(),x=read(),y=read();
if(op==1){
if(siz[fa(x)]<siz[fa(y)]) swap(x,y);
f[fa(y)]=fa(x),siz[x]+=siz[y];
}else{
if(fa(x)==fa(y)) printf("Y\\n");
else printf("N\\n");
}
}
return 0;
}

可撤销并查集（没有例题）

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+10;
int n,f[N],siz[N],q,op,x,y;
stack<pair<int,int> >stk;
int fa(int x){
if(f[x]==x) return x;
else return fa(f[x]);
}
signed main(){
cin>>n>>q;
for(int i=1;i<=n;i++) f[i]=i, siz[i]=1;
while(q–){
cin>>op;
if(op==1){
cin>>x>>y;
if(siz[fa(x)]<siz[fa(y)]) swap(x,y);
int X=fa(x),Y=fa(y);
stk.push({X,Y});
f[Y]=X, siz[X]+=siz[Y];
}else if(op==3){
x=stk.top().first, y=stk.top().second;
f[y]=y, siz[x]-=siz[y];
}else{
cin>>x>>y;
int X=fa(x),Y=fa(y);
if(X==Y) cout<<"Yes"<<'\\n';
else cout<<"No"<<'\\n';
}
}
return 0;
}

扩展域并查集

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e3+10;
int n,m,x,y,f[N],num[N],e[N],sl;
char op;
int fa(int x){
if(f[x]==x) return x;
else return f[x]=fa(f[x]);
}
signed main(){
cin>>n>>m;
for(int i=1;i<=n;i++) f[i]=i;
while(m–){
cin>>op>>x>>y;
if(op=='E'){
if(!e[x]) e[x]=y;
else{
int a=fa(e[x]),b=fa(y);
if(num[a]<num[b]) swap(a,b);
f[b]=a,num[a]+=num[b];
}
if(!e[y]) e[y]=x;
else{
int a=fa(e[y]),b=fa(x);
if(num[a]<num[b]) swap(a,b);
f[b]=a,num[a]+=num[b];
}
}else{
int a=fa(x),b=fa(y);
if(num[a]<num[b]) swap(a,b);
f[b]=a,num[a]+=num[b];
}
}
for(int i=1;i<=n;i++) if(f[i]==i) sl++;
cout<<sl;
return 0;
}//代码比较混乱，这里的e就是第二倍空间，这种写法也是可以的，但如果有很多条件就很费劲了

如果两人之间的关系不是相互的呢？那么我们就要使用强连通分量——tarjan了。