递增的三元子序列+进阶+实现

题目：

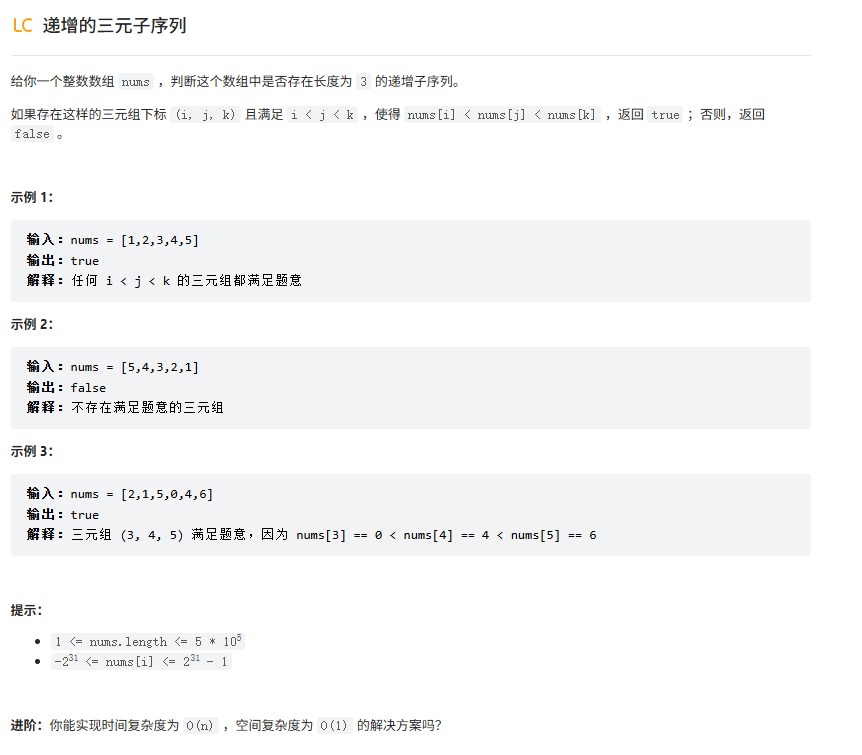
常规思考：

实现：

class Solution {
public:
bool increasingTriplet(vector<int>& nums) {
vector<int> min_left(nums.size(),INT_MAX);
vector<int> max_right(nums.size(),INT_MIN);

bool ret=false;

min_left[0]=nums[0];
for (int i=1;i<nums.size();i++)
{
min_left[i]=min(min_left[i–1],nums[i]);
}
max_right[nums.size()–1]=nums.back();
for (int i=nums.size()–2;i>–1;—i)
{
max_right[i]=max(max_right[i+1],nums[i]);
}

for (int i=0;i<nums.size();++i)
{
if (nums[i]>min_left[i]&&nums[i]<max_right[i])
{
ret=true;
break;
}
}

return ret;
}
};

进阶思考：

实现：

class Solution {
public:
bool increasingTriplet(vector<int>& nums) {
if (nums.size()<3) return false;
int l=nums[0];
int m=INT_MAX;

bool ret=false;
for (int i=1;i<nums.size();i++)
{
if(nums[i]>m)
{
ret=true;
break;
}
else if (nums[i]>l)
{
m=nums[i];
}
else
{
l=nums[i];
}
}

return ret;
}
};