1、简介
在过去的几年里,无数基于群体智能的元启发式算法被引入并广泛应用。尽管这些算法借鉴了生物行为,但它们相似的启发式范式和模块化设计导致了复杂优化问题中的不平衡探索和利用。将数学属性与随机搜索过程相结合的元启发式算法可以帮助突破传统的进化范式,增强个体优化。为了追求这一目标,本研究引入了一种基于数学的创新元启发式算法,称为亚当梯度下降优化器(AGDO),旨在解决持续优化和工程挑战。AGDO受到Adam优化器的启发,使用三个规则探索了整个搜索过程:渐进式梯度动量积分、动态梯度交互系统和系统优化算子。渐进式梯度动量积分和动态梯度交互系统很好地平衡了探索和开发,而系统优化算子则细化了开发方面。AGDO的性能,结合几个知名和新引入的元启发式,在CEC2017基准上跨各个维度和六个实际工程挑战进行了评估。Wilcoxon秩和检验证实了其功效。
2、提出的AGDO算法
本部分深入探讨了亚当优化算法背后的基本理论和原理。此外,深入阐述了亚当梯度下降优化器(AGDO)的灵感,详细介绍了其优化过程和关键机制。
2.1 动机
随机梯度优化在许多科学和工程学科中具有重要的实用价值。这些领域的许多问题可以简化为优化参数目标函数,目标是最大化或最小化特定标量值79。当目标函数可以与其参数相区别时,梯度下降成为一种有效的优化技术,因为计算所有参数的一阶偏导数在计算上类似于评估函数本身80。然而,在现实中,目标函数往往是随机的,具有不确定性和波动性。2014年,一阶方法Adam被提出来处理高维参数空间中的随机目标优化问题。Adam技术是一种高效的随机优化方法,只需要一阶梯度和最少的内存使用。Adam,“自适应矩估计”的缩写,通过评估梯度的第一和第二矩来计算每个参数的唯一学习率。Adam方法结合了两种流行方法的优势:AdaGrad和RMSProp。AdaGrad在稀疏梯度82上表现良好,而RMSProp在在线和非平滑设置83。平滑目标,处理稀疏梯度的能力,以及一种步进退火形式的自然执行。这些特性使Adam方法成为许多学习机器和深度学习应用中强大的优化工具。
2.2 梯度下降法(GDM)
梯度下降算法是一种用于定位目标函数局部最小值的主要优化技术,它被广泛用于机器学习和深度学习。梯度下降方法背后的核心思想是利用目标函数的梯度数据来指导位置的更新。特别是,梯度指示目标函数在给定点的最陡增长路径,而向梯度的反向移动导致目标函数的最快下降。我们在梯度的反向重复调整以定位函数的局部最小值。
为了更好地理解梯度下降法(GDM),我们需要定义需要最小化的目标函数f(x)f(x)f(x)。这里x=[x1,x2,…,xn]x = [x_1, x_2, \\ldots, x_n]x=[x1,x2,…,xn]表示一个n维向量,目标是找到能使f(x)f(x)f(x)值最小的xxx。目标函数的斜率表示为一个向量(见图2)。图中的θ\\thetaθ(即xxx)表示函数对每个变量的变化率:
∇J(x)=[∂f(x)∂x1,∂f(x)∂x2,⋯ ,∂f(x)∂xn](1)\\nabla J(x) =
\\begin{bmatrix}
\\frac{\\partial f(x)}{\\partial x_1}, & \\frac{\\partial f(x)}{\\partial x_2}, & \\cdots, & \\frac{\\partial f(x)}{\\partial x_n}
\\end{bmatrix} \\tag{1}∇J(x)=[∂x1∂f(x),∂x2∂f(x),⋯,∂xn∂f(x)](1)
其中∇J(x)\\nabla J(x)∇J(x)表示当前位置损失函数J(x)J(x)J(x)的梯度。
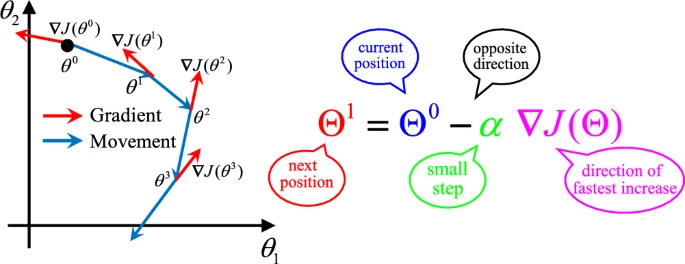
图1 GDM更新方向及其原理
在机器学习领域,常用的损失函数是均方误差(MSE),它量化了预测值与实际结果之间的差异。MSE是一个凸函数,可以使用梯度下降法(GDM)来最小化这个损失函数以找到最优位置。MSE关于位置xxx的梯度为:
∇J(x)=2m∑i=1m(h(x,x(i))−yi)⋅∇xh(x,x(i))(2)\\nabla J(x)=\\frac{2}{m}\\sum\\nolimits_{i=1}^{m}\\left(h\\left(x,x^{(i)}\\right)-y_{i}\\right)\\cdot\\nabla_{x}h\\left(x,x^{(i)}\\right)\\tag{2}∇J(x)=m2∑i=1m(h(x,x(i))−yi)⋅∇xh(x,x(i))(2)
这里mmm表示样本数量,yiy_{i}yi表示第iii个样本的实际值,函数的预测值y^j\\hat{y}_{j}y^j即y^i=h(x,x(i))\\hat{y}_{i}=h\\left(x,x^{(i)}\\right)y^i=h(x,x(i))。此外,x(i)x^{(i)}x(i)是对应于第iii个样本的位置向量。
为了确定从当前点移动的距离,将步长α\\alphaα乘以损失函数的梯度:
下降距离=α⋅∂∂xiJ(x1,x2,…,xn)(3){\\rm 下降距离}=\\alpha\\cdot\\frac{\\partial}{\\partial x_{i}}J(x_{1},x_{2},\\ldots,x_{n})\\tag{3}下降距离=α⋅∂xi∂J(x1,x2,…,xn)(3)
梯度下降的基本思想是沿着目标函数梯度的相反方向移动来更新位置。假设xtx_{t}xt是第ttt次迭代的位置向量,在每次迭代步骤中,根据梯度的负方向更新位置,梯度下降法的最终更新公式为:
Xt+1=xt−α⋅∇J(x)(4)X_{t+1}=x_{t}-\\alpha\\cdot\\nabla J(x)\\tag{4}Xt+1=xt−α⋅∇J(x)(4)
实际上,梯度下降法(GDM)面临着几个问题,包括鞍点问题,在某些情况下会阻碍找到全局最优解。鞍点出现在目标函数梯度等于零但该点不是局部最小值或最大值的位置。鞍点在某些方向上表现为最小值,在其他方向上表现为最大值或平坦区域(图3)。鞍点的存在导致GDM停滞不前,因为在鞍点处梯度为零,导致位置更新停止。此外,在鞍点附近,梯度的变化非常小,导致更新步长极小,使得GDM的收敛速度显著减慢。
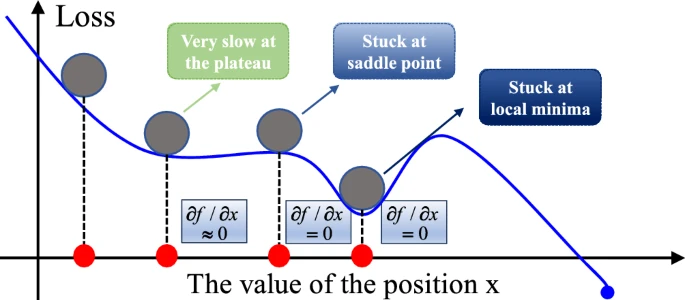
图2 鞍点功能演示
在GDM就像我们徒步旅行时采取的步骤大小,我们可以使用α\\alphaα控制好我们每一步走的距离,确保我们不会走太大的一步,其实就是不要走得太快而早早疲劳(陷入局部最优)而错过最低点;同时,我们还需要确保我们不要走得太慢(收敛速度太慢),导致太阳已经下山,还没有走到山底。
3 Adam梯度下降优化器(AGDO)
提出的AGDO算法通过以下方式实现更高效的全局搜索和优化:应用GDM进行位置信息搜索和方向引导,采用渐进梯度动量整合策略进行探索,并通过动态梯度交互系统和系统优化算子优化开发过程。
3.1 初始化
优化问题的背景是处理无约束单目标优化任务,旨在识别整个定义域R\\mathbb{R}R内使目标函数最大或最小的变量组合。问题定义如下:
minx:RN×Dmf(x)(5)\\min_{x:\\mathbb{R}^{N\\times Dm}} f(x)\\tag{5}x:RN×Dmminf(x)(5)
其中f(x)f(x)f(x)是要最小化的适应度函数,x=[xij]∈RN×Dimx=[x_{ij}]\\in\\mathbb{R}^{N\\times Dim}x=[xij]∈RN×Dim是待优化的变量矩阵,xijx_{ij}xij表示优化向量(即第jjj维中第iii个个体向量),DimDimDim表示待优化问题的维度。每个xijx_{ij}xij的取值受以下条件约束:
LBj≤xij≤UBj ∀i=1,2 , N, ∀j=1,2,…,Dim(6)LB_{j}\\leq x_{ij}\\leq UB_{j}\\ \\forall i=1,2\\ ,\\ N,\\ \\forall j=1, 2,\\ldots,Dim\\tag{6}LBj≤xij≤UBj ∀i=1,2 , N, ∀j=1,2,…,Dim(6)
LBj=[LB1,LB2,…,LBDim] ,UBj=[UB1,UB2,…,UBDim]LB_{j}=[LB_{1},LB_{2},\\ldots,LB_{Dim}]\\ ,UB_{j}=[UB_{1},UB_{2},\\ldots,UB_{Dim}]LBj=[LB1,LB2,…,LBDim] ,UBj=[UB1,UB2,…,UBDim]
式(6)中,LBjLB_{j}LBj是优化变量第jjj维的下界向量,UBjUB_{j}UBj是相应的上界向量。与其他元启发式算法类似,AGDO从在候选解边界内生成初始随机种群开始,以探索最优解。考虑到问题的群体性质,种群规模为NNN,每个种群个体由模糊优化变量或向量组成。因此,使用式(7)生成随机种群:
xij=rand(N,Dim)×(UBj−LBj)+LBj(7)x_{ij}=rand(N,Dim)\\times(UB_{j}-LB_{j})+LB_{j}\\tag{7}xij=rand(N,Dim)×(UBj−LBj)+LBj(7)
其中xijx_{ij}xij表示种群中第iii个个体在第jjj维的位置数据,rand(N,Dim)rand(N,Dim)rand(N,Dim)是一个N×DimN\\times DimN×Dim的矩阵,填充有0到1之间的随机值。式(8)提供了综合优化挑战的矩阵模型,能够说明种群在不同维度上的结构,清晰描述优化过程中种群的多样性和个体的空间分布。
Xn=[x1,1×1,2⋯x1,Dimx2,1×2,2⋯x2,Dim⋮⋮⋱⋮xN,1xN,2⋯xN,Dim]N×Dim(8)X_{n}=\\begin{bmatrix}x_{1,1}&x_{1,2}&\\cdots&x_{1,Dim}\\\\ x_{2,1}&x_{2,2}&\\cdots&x_{2,Dim}\\\\ \\vdots&\\vdots&\\ddots&\\vdots\\\\ x_{N,1}&x_{N,2}&\\cdots&x_{N,Dim}\\end{bmatrix}_{N\\times Dim}\\tag{8}Xn=x1,1x2,1⋮xN,1x1,2x2,2⋮xN,2⋯⋯⋱⋯x1,Dimx2,Dim⋮xN,DimN×Dim(8)
开始时,AGDO将适应度得分最高的个体识别为最优个体,作为梯度下降方向的近似指导。具体来说,对于最小化问题,优势个体的位置是当前找到的全局最优解的近似值。通过选择适应度值最小的个体作为初始优势位置,算法能够在早期快速逼近最优解。初始优势位置XsuperiorX_{\\text{superior}}Xsuperior的公式如下:
fbest=min(f(Xi))(9)f_{best}=\\min\\left(f\\left(X_{i}\\right)\\right)\\tag{9}fbest=min(f(Xi))(9)
Xsuperior=X(argmin(f(Xi)))(10)X_{\\text{superior}}=X\\left(\\arg\\min\\left(f\\left(X_{i}\\right)\\right)\\right)\\tag{10}Xsuperior=X(argmin(f(Xi)))(10)
其中argmin运算符用于找到具有最小适应度值的个体的索引。
3.2 渐进梯度动量整合
渐进梯度动量整合是一种专为探索阶段设计的技术,其灵感主要来自Adam优化器中使用的梯度动量(一阶矩估计)。该阶段基于动量调整的动态特性,采用渐进式动量策略,从而形成创新的位置更新框架。该框架主要通过系统调整位置系数来发现潜在更优解,以提高算法的全局搜索效率。与固定动量策略不同,渐进梯度动量整合通过逐步调整位置系数来适应优化过程的变化。这种自适应系统通过综合考虑当前搜索状态和历史位置数据,实现实时位置调整。经渐进梯度动量整合后的新位置如式(11)所示:
X1,sumt+1={ω∗Xkt+αt∗Xktk=1Xkt+sin(2π∗dim∗t)∗X1,sumt+11<k<2/dim(11)X_{1,\\text{sum}}^{t+1}=\\begin{cases}
\\omega*X_{k}^{t}+\\alpha_{t}*X_{k}^{t} & k=1 \\\\
X_{k}^{t}+\\sin(2\\pi*\\dim*t)*X_{1,\\text{sum}}^{t+1} & 1<k<2/\\dim
\\end{cases}\\tag{11}X1,sumt+1={ω∗Xkt+αt∗XktXkt+sin(2π∗dim∗t)∗X1,sumt+1k=11<k<2/dim(11)
其中XktX_{k}^{t}Xkt表示第ttt次迭代时搜索代理的位置,ttt表示连续梯度动量整合的次数,该参数根据优化问题的维度不断变化以适应不同场景下的问题复杂度。
情况1:在预探索阶段,过于频繁的动量调整可能导致不必要的计算开销和优化过程中的振荡。通过将次数kkk设为1,并按照式(11)前半部分更新位置,渐进梯度动量整合方法能在减少计算资源浪费的同时保持较快的收敛速度。这种调整机制使算法在处理简单问题时更加高效。式(11)中的ω\\omegaω和αt\\alpha_{t}αt分别如式(12)和(13)所示:
ω=rand()∗(1ttotalβinov−2ttotaltinov+12)(12)\\omega=rand()*\\left(\\frac{1}{t_{\\text{total}}}\\beta_{\\text{inov}}-\\frac{2}{t_{\\text{total}}}t_{\\text{inov}}+\\frac{1}{2}\\right)\\tag{12}ω=rand()∗(ttotal1βinov−ttotal2tinov+21)(12)
αt=cos(1−rand()∗2π)(13)\\alpha_{t}=\\cos(1-rand()*2\\pi)\\tag{13}αt=cos(1−rand()∗2π)(13)
图4展示了ω\\omegaω随迭代次数增加的动态变化过程。初始时在[−0.5,0.5][-0.5,0.5][−0.5,0.5]范围内随机调整,随着迭代进行,其值开始缓慢减小。这种逐步减小的设计旨在让算法逐渐缩小搜索区域,集中到更优区域进行彻底检查。非线性下降过程保证了搜索范围的逐步收敛,同时保留一定探索能力以避免陷入局部最优。αt\\alpha_{t}αt的计算方式通过引入随机角度并将其映射到[−1,1][-1,1][−1,1]范围,为位置更新增加了随机性元素,有助于在搜索空间中引入更多变化和探索。在算法初始阶段,增强的随机性有利于进行全面探索。
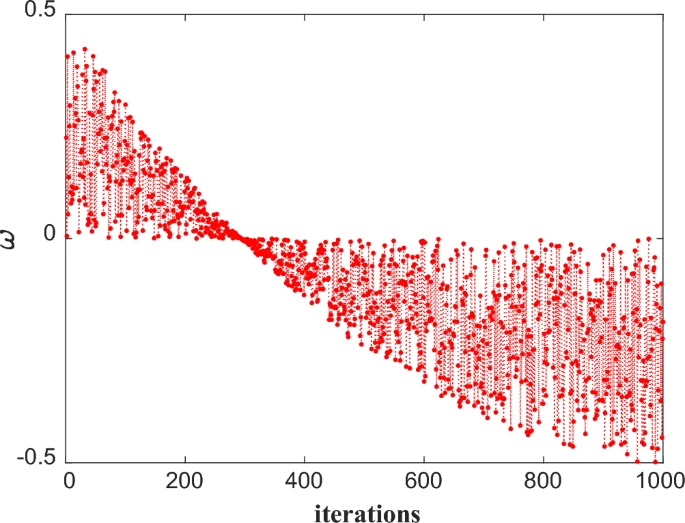
图4 动态w调整趋势
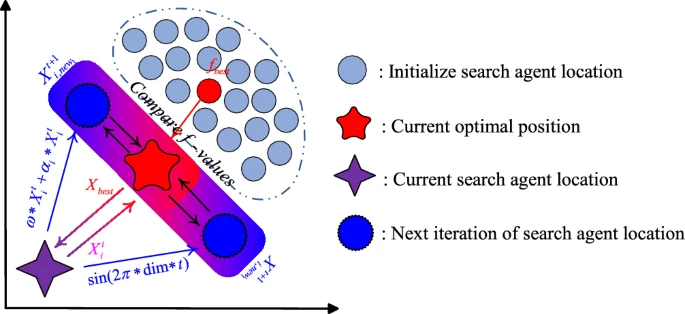
图5 渐进式梯度动量积分更新过程
3.3 动态梯度交互系统
受Adam优化器中二阶矩估计的启发,动态梯度交互系统在AGDO的开发阶段起着关键作用。通过采用类似的二阶矩估计技术,确保优化过程中高效开发和稳定收敛。初始位置的选择也是该系统的关键步骤,不仅利用原始初始化生成的种群位置,还通过"randperm"函数随机生成另外N个初始位置,保证初始位置在解空间中均匀且唯一分布,为优化过程提供多样化的起点。在第t次迭代中,使用随机生成的初始位置索引持续为系统提供全新初始位置,选择前两个索引(Xidx1X_{idx1}Xidx1和Xidx2X_{idx2}Xidx2)确保从不同起始位置开始优化,从而增强解空间的探索能力,具体选择如式(14)所示:
Xidx1=Xrp(1)t(14)X_{idx1} = X_{rp(1)}^{t} \\tag{14}Xidx1=Xrp(1)t(14)
Xidx2=Xrp(2)tX_{idx2} = X_{rp(2)}^{t}Xidx2=Xrp(2)t
其中rp(1)rp(1)rp(1)和rp(2)rp(2)rp(2)是"randperm"随机生成的前两个整数。
在动态梯度交互系统中,搜索方向的确定对AGDO性能至关重要。方向指针在此方面发挥重要作用,用于确定下一个搜索方向,其公式如下:
ϵ=f(Xidx2)−f(Xidx1)∣f(Xidx2)−f(Xidx1)∣(15)\\epsilon = \\frac{f(X_{idx2})-f(X_{idx1})}{|f(X_{idx2})-f(X_{idx1})|} \\tag{15}ϵ=∣f(Xidx2)−f(Xidx1)∣f(Xidx2)−f(Xidx1)(15)
其中ϵ\\epsilonϵ是系统方向指针,f(Xidx2)f(X_{idx2})f(Xidx2)是初始位置的系统重新生成适应度值,f(Xidx1)f(X_{idx1})f(Xidx1)是初始化生成的适应度值。方向指针通过归一化将适应度值差异转换为1或-1,保证方向选择不受适应度值大小影响,从而实现更稳定和统一的更新步长。系统通过计算每对位置的适应度差异,基于归一化方向指示器实时调整搜索方向,使优化算法能准确选择更优方向移动,有效引导搜索过程逐步接近全局最优解。这种机制使动态梯度交互系统在复杂解空间中保持高效开发和稳定收敛。系统将位置更新分为开发前和开发后两个阶段,能更好适应过程的不同需求。
情况1:在开发前阶段,系统主要任务是广泛探索解空间,目标是通过多样化搜索策略发现潜在高质量解并避免陷入局部最优。为此系统采用复杂更新方法引导搜索方向,具体见式(16):
Xi,new1t=Xit+ϵ∗α∗(G−Xidx1t)−α∗(Xidx2t−Xit)(16)X_{i,new1}^{t} = X_{i}^{t} + \\epsilon * \\alpha * (G – X_{idx1}^{t}) – \\alpha * (X_{idx2}^{t} – X_{i}^{t}) \\tag{16}Xi,new1t=Xit+ϵ∗α∗(G−Xidx1t)−α∗(Xidx2t−Xit)(16)
其中α\\alphaα是由动态缩放因子(1−ηt)(1-\\eta_t)(1−ηt)确定的随机扰动向量,范围在[0,(1−ηt)][0,(1-\\eta_t)][0,(1−ηt)]内,α\\alphaα通过式(17)变化。GGG通过矩估计寻找最优位置,估计原理如式(17)所示:
α=(1−ηt)∗rand(1,Dim)(17)\\alpha = (1-\\eta_t) * rand(1,Dim) \\tag{17}α=(1−ηt)∗rand(1,Dim)(17)
在位置更新方法的初始阶段,系统整合多种位置数据广泛探索解空间,有助于早期快速识别有希望区域,特别是当解空间大部分未被探索时。通过使当前位置动态适应多个方向,算法能避免因过早收敛而错过其他可能高质量解。α\\alphaα的引入在当前位置和多个参考位置间取得平衡,确保系统在开发过程中能找到合理折衷,避免过度依赖特定位置,从而提高优化的全面性和效率。
情况2:进入开发后阶段后,系统目标转向精细调整以保证解质量和稳定收敛。该阶段策略聚焦于快速引导当前解接近最优解,优化搜索过程变得更高效和集中,具体更新公式如式(18)所示:
Xi,new2t=Xit+α∗(G−Xidx1t)(18)X_{i,new2}^{t} = X_{i}^{t} + \\alpha * (G – X_{idx1}^{t}) \\tag{18}Xi,new2t=Xit+α∗(G−Xidx1t)(18)
系统利用索引位置直接调整到最优解方向,这种直接高效的修改显著加速算法收敛,特别是当解空间接近全局最优时。由于更新方法相对简单,降低了计算需求,使算法能在最终优化阶段有效微调,从而保证更精确的收敛。
在动态梯度交互系统中,位置GGG是关键参考点,在优化过程中起核心作用,由矩估计方法确定,主要用于引导和调整搜索过程,具体定义如式(19):
G=Xi,bestt−η∗mtvt+ϵ(19)G = X_{i,best}^{t} – \\frac{\\eta * m_{t}}{\\sqrt{v_{t}} + \\epsilon} \\tag{19}G=Xi,bestt−vt+ϵη∗mt(19)
其中Xi,besttX_{i,best}^{t}Xi,bestt表示第t步最优解的当前位置,η\\etaη设为0.001的学习率,vtv_{t}vt是迭代期间二阶矩的偏差校正估计,ϵ\\epsilonϵ是极小常数(1e-8)避免除以零,mtm_{t}mt是梯度的偏差校正估计。vtv_{t}vt和mtm_{t}mt的表达式如下:
vt=vt1−β2t(20)v_{t} = \\frac{v_{t}}{1-\\beta_2^t} \\tag{20}vt=1−β2tvt(20)
mt=mt1−β1tm_{t} = \\frac{m_{t}}{1-\\beta_1^t}mt=1−β1tmt
式(20)中,mtm_{t}mt和vtv_{t}vt分别表示梯度一阶和二阶矩估计,β1\\beta_1β1和β2\\beta_2β2表示这些矩估计的指数衰减率,通常取值0.9和0.999。它们的更新方程如下:
vt=β2∗vt−1+(1−β2)∗gt2(21)v_{t} = \\beta_2 * v_{t-1} + (1-\\beta_2)*g_{t}^2 \\tag{21}vt=β2∗vt−1+(1−β2)∗gt2(21)
mt=β1∗mt−1+(1−β1)∗gtm_{t} = \\beta_1 * m_{t-1} + (1-\\beta_1)*g_{t}mt=β1∗mt−1+(1−β1)∗gt
其中gtg_{t}gt是第t次迭代计算的位置梯度信息,由式(22)确定:
gt=Xi,bestt−C∗P(22)g_{t} = X_{i,best}^{t} – C * P \\tag{22}gt=Xi,bestt−C∗P(22)
Xi,besttX_{i,best}^{t}Xi,bestt是当前最优解位置,即在第t次迭代中找到的最优解。CCC和PPP的数学公式如下:
P=Xi,meant−Xi,new1t(23)P = X_{i,mean}^{t} – X_{i,new1}^{t} \\tag{23}P=Xi,meant−Xi,new1t(23)
C=1−rand()C = 1 – rand()C=1−rand()
其中Xi,meantX_{i,mean}^{t}Xi,meant是当前位置的均值信息,与渐进梯度动量整合中的更新位置信息结合,为梯度信息提供参考方向。CCC是区间[0,1]内的随机调整因子,确保梯度调整步骤的随机性和多样性。
动态梯度交互系统位置更新的最终公式如式(24)所示:
Xi,newt={Xi,new1trand()>ηXi,new2t否则(24)X_{i,new}^{t} = \\begin{cases}
X_{i,new1}^{t} & rand() > \\eta \\\\
X_{i,new2}^{t} & \\text{否则}
\\end{cases} \\tag{24}Xi,newt={Xi,new1tXi,new2trand()>η否则(24)
信赖域策略确实是动态梯度交互系统中的重要考量,主要用于通过确保每次迭代的位置更新不会过大来控制优化步调,避免可能的不稳定和低效搜索。系统通过接受或拒绝更新位置来调整信赖域,确保高效探索解空间而不会过度偏离,从而提高优化系统的有效性和鲁棒性。
信赖域策略包含两部分:位置更新判断和最优位置更新。首先考虑位置更新的条件:
Xit+1={Xi,newt如果 f(Xi,newt)<f(Xit)Xit否则(25)X_{i}^{t+1} = \\begin{cases}
X_{i,new}^{t} & \\text{如果 } f(X_{i,new}^{t}) < f(X_{i}^{t}) \\\\
X_{i}^{t} & \\text{否则}
\\end{cases} \\tag{25}Xit+1={Xi,newtXit如果 f(Xi,newt)<f(Xit)否则(25)
这意味着当新位置的适应度函数值优于当前位置XitX_{i}^{t}Xit时接受新位置。接下来考虑最优位置的更新:
Xbestt+1={Xit+1如果 f(Xit+1)<f(Xbestt)Xbestt否则(26)X_{best}^{t+1} = \\begin{cases}
X_{i}^{t+1} & \\text{如果 } f(X_{i}^{t+1}) < f(X_{best}^{t}) \\\\
X_{best}^{t} & \\text{否则}
\\end{cases} \\tag{26}Xbestt+1={Xit+1Xbestt如果 f(Xit+1)<f(Xbestt)否则(26)
这样,信赖域策略确保动态梯度交互系统在开发过程中能探索新的更优解,同时保持解的稳定性并避免过度偏离。动态梯度交互系统的更新过程如图6所示。
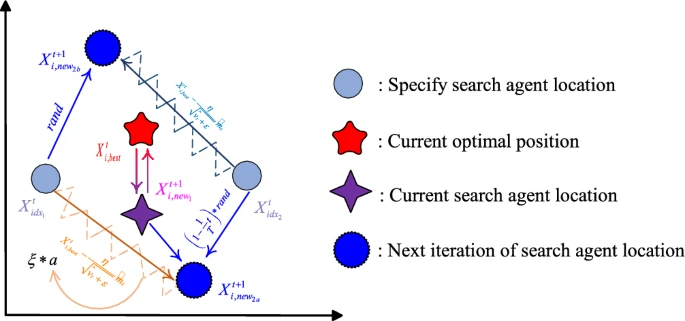
图6 动态梯度交互系统更新过程
3.4 系统优化算子
在动态梯度交互系统的开发阶段,虽然系统已展现出优异的优化搜索能力,但在解空间的整体开发上仍可能存在不足。为解决这些问题,系统优化算子阶段强调全局优化方法和引导策略,通过引入关键飞行策略共同增强解空间探索能力,使系统能进行更广泛的搜索并提升整体性能。其运算公式如式(27)所示:
Xk1,k2,…1,km=Xm1,m2+k1exp(ϕ)+δ∗(Xm1,m2−Xi∗+θ)(27)X_{k_1,k_2,\\ldots}^{1,k_m} = X_{m_1,m_2} + k_1 \\exp(\\phi) + \\delta * (X_{m_1,m_2} – X_i^* + \\theta) \\tag{27}Xk1,k2,…1,km=Xm1,m2+k1exp(ϕ)+δ∗(Xm1,m2−Xi∗+θ)(27)
δf rand S=[1+e(Δ2)2]−1(28)\\delta f \\text{ rand } S = \\left[ 1 + e^{\\left( \\frac{\\Delta}{2} \\right)^2} \\right]^{-1} \\tag{28}δf rand S=[1+e(2Δ)2]−1(28)
其中Xm1,m2X_{m_1,m_2}Xm1,m2表示倾斜迭代中的最优操作位置,k1exp(ϕ)k_1 \\exp(\\phi)k1exp(ϕ)表示Levy飞行函数,通过式(29)计算:
k1exp(ϕ)=0.01×1∣x∣×Tn(29)k_1 \\exp(\\phi) = 0.01 \\times \\frac{1}{|x|} \\times \\frac{T}{\\sqrt{n}} \\tag{29}k1exp(ϕ)=0.01×∣x∣1×nT(29)
式(28)中σ\\sigmaσ是0到2的随机变量(本文取σ=15\\sigma = 15σ=15),r1r_1r1和r2r_2r2是0到1的任意数。rrr的计算公式为:
r=Γ(1+σ)×sin(πθ2)Γ(1+σ2)×σ×π2211/4(30)r = \\frac{\\Gamma \\left( 1 + \\sigma \\right) \\times \\sin\\left(\\frac{\\pi\\theta}{2}\\right)}{\\Gamma \\left(\\frac{1+\\sigma}{2}\\right) \\times \\sigma \\times \\frac{\\pi^{2}}{2}} \\quad 1^{1/4} \\tag{30}r=Γ(21+σ)×σ×2π2Γ(1+σ)×sin(2πθ)11/4(30)
系统优化算子中δ\\deltaδ和θ\\thetaθ的数学表达式分别如式(31)和(32)所示:
δ=rand(1+1τrandttest−2τtestttest+1)(31)\\delta = \\text{rand} \\left( 1 + \\frac{1}{\\tau_{\\text{rand}}} t_{\\text{test}} – \\frac{2}{\\tau_{\\text{test}}} t_{\\text{test}} + 1 \\right) \\tag{31}δ=rand(1+τrand1ttest−τtest2ttest+1)(31)
θ=2ttestτtest(32)\\theta = \\frac{2t_{\\text{test}}}{\\tau_{\\text{test}}} \\tag{32}θ=τtest2ttest(32)
其中θ\\thetaθ是[0, 2]范围内的线性递增函数。
图2展示了不同迭代次数下的行为变化。根据图示,δ\\deltaδ在[0,1]区间内经历接近0的非线性下降过程,其中包含随机扰动。这种关键波动机制使算子能更专注于广泛搜索策略,从而探索更大的解空间;而在新方案中,下降过程允许逐步过渡到局部区域,同时保持解空间探索。动态变化与随机扰动的结合帮助算子优化动态梯度交互系统的探索过程,避免过早陷入局部最优,并确保全局搜索后的精确收敛。
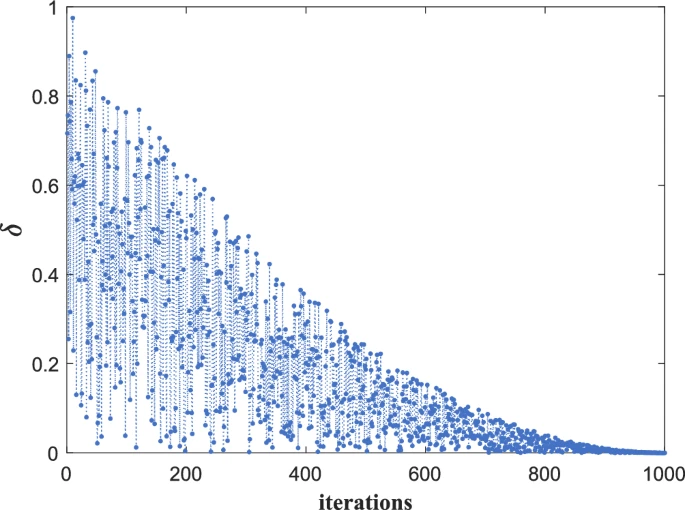
图2 δ\\deltaδ变化趋势
系统优化算子旨在显著提升解空间开发和优化效率。通过引入Levy飞行,弥补了开发阶段的探索不足。通过动态调整搜索策略并灵活切换全局与局部搜索,该阶段确保优化过程在相对优化解空间时能逐步精确收敛至最优解。算子增强了系统的全局搜索功能并优化局部调整,大幅提升整体搜索效率和精度,保证解空间的全面覆盖和最优解的有效识别。
3.5 AGDO算法执行流程
本部分深入探讨AGDO的探索与开发阶段。首先,算法精心生成多组集合以启动优化过程。随后通过渐进梯度动量整合技术逐步修正定位难点,识别高质量解,从而完成探索阶段。在动态梯度交互框架内,采用新颖的起始位置保证优化从独特点开始,提升算法全局搜索效率。此外引入起始区域方法确保解的稳定性,防止动态梯度交互系统出现显著偏差。最终,系统增强算子(术语AGDO的开发阶段)通过整合Levy飞行,提升算法在局部搜索中的精度和多样性。算法详细伪代码见算法3.1,流程图见图3。这些细节不仅说明AGDO算法的设计原理,更突出其在探索与开发阶段的独特实现和优化技术。
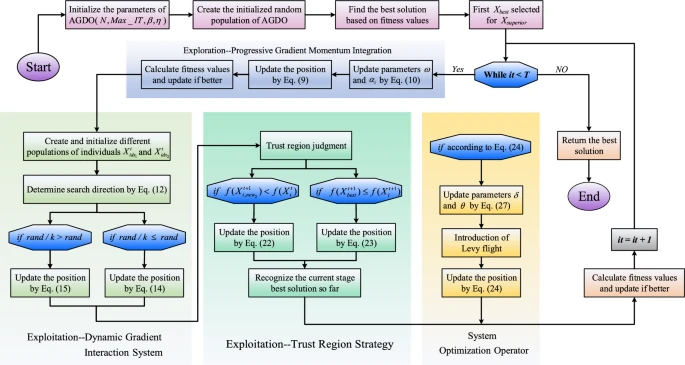
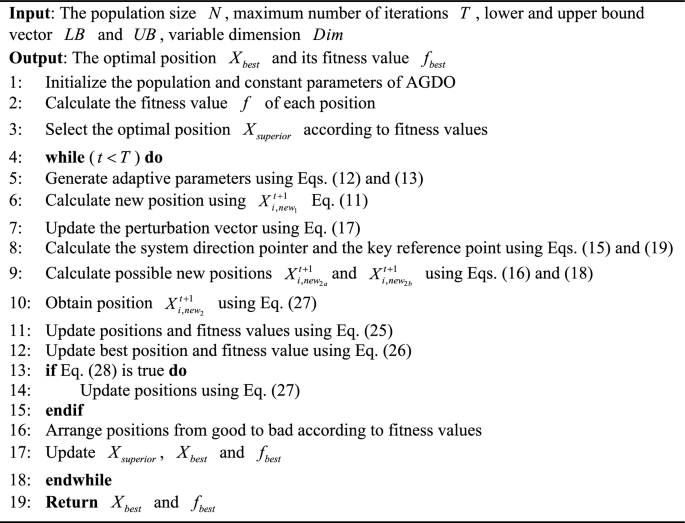
4 完整代码
function [fbest, pbest, cg] = AGDO(N,T, lb, ub, dim,fobj)
VarSize = [1 dim];% Dimension of the problem
beta1 = 0.9; % Exponential decay rates of biased first original moment estimates
beta2 = 0.999; % Exponential decay rates of biased second original moment estimates
epsilon = 1e-8;% Tiny constant for avoiding division by zero
m = zeros(N, dim);% Initial estimate of the deviation of the gradient
v = zeros(N, dim);% Initial estimate of the deviation of the second-order moments
lr = 0.001; % Learning rate
alpha = cos((1–rand(N,1))*2*pi); % Eq.(13)
fit = zeros(N, 1);% Fitness of each individual
bestpos = zeros(1, dim);% Best position
fbest = inf;%Best score (initially infinite)
po = initialization(N, dim, ub, lb);% Initialize population
%% Record the initial optimal solution and fitness
for i = 1:N
fit(i) = fobj(po(i, :));
if fit(i) <= fbest
bestpos = po(i, :);
fbest = fit(i);
end
end
cg = zeros(1, T);% Store convergence information
%% Main optimization loop
for t = 1:T
w = rand()*((1/T^2)*t^2–2/T*t+1/2); % Eq.(12)
a = (1 – t/T) * rand(VarSize); % Eq.(17)
xi = rand()*((1/T^2)*t^2–2/T*t+1); % Eq.(31)
for i = 1:N
for k = 1:dim/2
% Eq.(11)
if k == 1
npo_line = w .* po(i, :) + alpha(i) .* po(i, :);
else
npo_line = po(i, :) + (sin(2*pi*dim*t) ) .* npo_line;
end
A1 = randperm(N);
A1(A1 == i) = [];
% Eq.(14)
a1 = A1(1);
a2 = A1(2);
% Eq.(15)
zeta = ((fit(a1) – fit(i)) / abs(fit(a1) – fit(i)));
po_mean = mean(po);
P = (po_mean – npo_line);% Eq.(23) (first-order)
f = gtdt(bestpos, P, lr, t, beta1, beta2, epsilon, m, v);
npo_1a = npo_line + zeta *a.*(f – po(a1, :)) – a.*(npo_line – po(a2, :));% Eq.(16)
npo_1b = po(a1, :) + a .* (f – po(a2, :));% Eq.(18)
for j = 1:dim
if rand/k > rand
npo_line(1, j) = npo_1b(1, j);
else
npo_line(1, j) = npo_1a(1, j);
end
end
npo_line = max(npo_line, lb);
npo_line = min(npo_line, ub);
newfit = fobj(npo_line);
if newfit < fit(i)
po(i, :) = npo_line;
fit(i) = newfit;
if fit(i) <= fbest
bestpos = po(i, :);
fbest = fit(i);
end
end
a = rand(VarSize);% Eq.(17)
end
end
if rand <= 1/(1+exp(–(18*(t/T)–12)))
Step_length=levy(N, dim, 1.2);
Elite=repmat(bestpos, N, 1);
for i=1:N
for j=1:dim
npo_2(i,j)=Elite(i,j)+Step_length(i,j)*xi*(Elite(i,j)–po(i,j)*(2*t/T)); % Eq.(27)
end
end
po = npo_2;
po = max(po, lb);
po = min(po, ub);
end
%% Evaluation
for i=1:N
newfit(1, i)=fobj(po(i, :));
end
[fbestN, sorted_indexes] = sort(newfit);
po = po(sorted_indexes(1:N), :);
if fbestN(1)<fbest
bestpos = po(1,:);
fbest=fbestN(1);
end
%% Record convergence curve
cg(t) = fbest;
pbest = bestpos;
end
end
% Initialization function
function X = initialization(N, Dim, UB, LB)
B_no = size(UB, 2); % number of boundaries
if B_no == 1
X = rand(N, Dim) .* (UB – LB) + LB;
end
% If each variable has a different lb and ub
if B_no > 1
X = zeros(N, Dim);
for i = 1:Dim
Ub_i = UB(i);
Lb_i = LB(i);
X(:, i) = rand(N, 1) .* (Ub_i – Lb_i) + Lb_i;
end
end
end
% Enhanced Gradient Descent with Adam and Momentum
function f = gtdt(X, P, lr, t, beta1, beta2, epsilon, m, v)
C = 1 – rand;
grad = X – C .* P;
%Eq.(21)
m = beta1 * m + (1 – beta1) * grad;% Updating biased first moment estimates
v = beta2 * v + (1 – beta2) * (grad .^ 2);% Updating biased second original moment estimates
%Eq.(20)
m_hat = m / (1 – beta1 ^ t);% Calculation of bias-corrected first moment estimates
v_hat = v / (1 – beta2 ^ t);% Calculate bias-corrected second original moment estimates
%Eq.(19)
f = X – lr * m_hat ./ (sqrt(v_hat) + epsilon);
end
function [z] = levy(n,m,beta)
% beta is set to 1.5 in this paper
num = gamma(1+beta)*sin(pi*beta/2);
den = gamma((1+beta)/2)*beta*2^((beta–1)/2);
sigma_u = (num/den)^(1/beta); % Eq.(30)
u = random('Normal',0,sigma_u,n,m);
v = random('Normal',0,1,n,m);
z =u./(abs(v).^(1/beta)); % Eq.(29)
end
Xia, Y., Ji, Y. Application of a novel metaheuristic algorithm inspired by Adam gradient descent in distributed permutation flow shop scheduling problem and continuous engineering problems. Sci Rep 15, 21692 (2025). https://doi.org/10.1038/s41598-025-01678-9
 网硕互联帮助中心
网硕互联帮助中心



评论前必须登录!
注册