java学习之数据结构：四、树（代码补充）

这部分主要是用代码实现有序二叉树、树遍历、删除节点

目录

1.构建有序二叉树

1.1原理

 1.2插入实现

2.广度优先遍历–队列实现

3.深度优先遍历–递归实现

3.1先序遍历

3.2中序遍历

3.3后序遍历

4.删除

4.1删除叶子节点

4.2删除有一棵子树的节点

4.3删除有两棵子树的节点

5.整体代码

1.构建有序二叉树

1.1原理

左边节点值小于父节点，右边节点值大于父节点，看下图

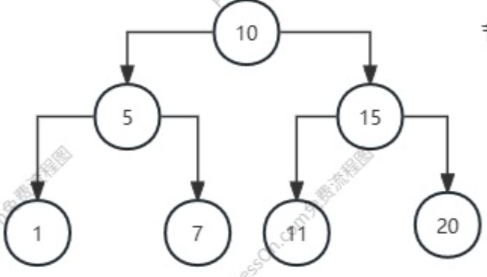
 1.2插入实现

当传入value值时，判断root节点是否为空：空的话建立新节点做root；不空，建立一个中间节点index，然后循环按照插入原理判断插到哪，代码如下：

public void insert(int value){
Node node = new Node(value);
if(root==null){
root = node;
return;
}
Node index = root;
while(true) {
if(index.value>value) {
//要插入的节点值小
if(index.left==null) {
//插入
index.left=node;
return;
}
index=index.left;
}else{
//要插入的节点值大
if(index.right==null){
index.right=node;
return;
}
index=index.right;
}
}

2.广度优先遍历–队列实现

广度优先遍历就是层次遍历，使用队列实现。当队列中进入一个新节点，输出后就找这个节点的左右孩子入队。

代码如下：

public void levelOrder() {
Queue<Node> queue = new LinkedList<Node>();
if(root!=null) {
queue.add(root);
}
Node index;
while (!queue.isEmpty()){
index = queue.poll();
System.out.print(index.value+Messages.getString("BinaryTree.0")); //$NON-NLS-1$
if(index.left!=null){
queue.add(index.left);
}
if(index.right!=null) {
queue.add(index.right);
}
}
System.out.println();
}

3.深度优先遍历–递归实现

3.1先序遍历

就是根-左-右的顺序，使用递归实现，代码如下：

/*
* 先序遍历
*/
public void beforeOrder(Node node){
if(node==null) {
return;
}
System.out.print(node.value+Messages.getString("BinaryTree.1"));
beforeOrder(node.left);
beforeOrder(node.right);
}

3.2中序遍历

使用左-根-右顺序

/*
* 中序遍历
*/
public void inOrder(Node node){
if(node==null){
return;
}
inOrder(node.left);
System.out.print(node.value+Messages.getString("BinaryTree.2")); //$NON-NLS-1$
inOrder(node.right);
}

3.3后序遍历

使用左-右-根顺序，代码如下：

/*
* 后序遍历
*/
public void afterOrder(Node node) {
if(node==null) {
return;
}
afterOrder(node.left);
afterOrder(node.right);
System.out.print(node.value+Messages.getString("BinaryTree.3"));
}

4.删除

删除比较复杂，要分三种情况：

4.1删除叶子节点

需要额外写一个函数来寻找父节点，代码如下：

/**
* 找目标值的父节点
*/
public Node searchParent(int value) {
if(root==null) {
return null;
}
Node index = root;
while (index!=null) {
if((index.left!=null&&index.left.value==value)||(index.right!=null&&index.right.value==value)) {
return index;
}else if (index.value>value) {
index=index.left;
}else {
index = index.right;
}

}
return null;
}

这部分代码如下：

if(target.left==null&&target.right==null) {
//叶子节点
//没有父节点
if(parent==null) {
root=null;
return;
}
//有父节点
if(parent.left!=null&&parent.left.value==value) {
parent.left=null;
}else {
parent.right=null;
}

}

4.2删除有一棵子树的节点

代码如下：

//有一棵子树的节点
//没有父节点
if(parent==null) {
//目标节点有左子树还是右子树
if(target.left!=null) {
root = root.left;
}else {
root=root.right;
}
return;
}
//有父节点
//判断目标节点是父节点的左孩子还是右孩子
if(parent.left!=null&&parent.left.value==value) {
//左孩子
//目标节点有左子树还是右子树
if(target.left!=null) {
parent.left = target.left;
}else {
parent.left = target.right;
}

}else {
//右孩子
//目标节点有左子树还是右子树
if(target.left!=null) {
parent.right = target.left;
}else {
parent.right = target.right;
}
}

4.3删除有两棵子树的节点

需要额外写一个判断最小值的函数：

/**
* 找树当中的最小值
*/
public int min(Node node) {
Node index = node;
while(index.left!=null) {
index=index.left;
}
return index.value;
}

代码如下：

if(target.left!=null&&target.right!=null) {
//有两棵子树的节点
int minVal = min(target.right);
delete(minVal);
target.value = minVal;

}

5.整体代码

代码如下：

package com.qcby.树;

import java.util.LinkedList;
import java.util.Queue;

public class BinaryTree {
Node root;
/**
* 插入
*/
public void insert(int value){
Node node = new Node(value);
if(root==null){
root = node;
return;
}
Node index = root;
while(true) {
if(index.value>value) {
//要插入的节点值小
if(index.left==null) {
//插入
index.left=node;
return;
}
index=index.left;
}else{
//要插入的节点值大
if(index.right==null){
index.right=node;
return;
}
index=index.right;
}
}
}
/*
* 广度优先遍历
*/
public void levelOrder() {
Queue<Node> queue = new LinkedList<Node>();
if(root!=null) {
queue.add(root);
}
Node index;
while (!queue.isEmpty()){
index = queue.poll();
System.out.print(index.value+Messages.getString("BinaryTree.0")); //$NON-NLS-1$
if(index.left!=null){
queue.add(index.left);
}
if(index.right!=null) {
queue.add(index.right);
}
}
System.out.println();
}
/*
* 先序遍历
*/
public void beforeOrder(Node node){
if(node==null) {
return;
}
System.out.print(node.value+Messages.getString("BinaryTree.1")); //$NON-NLS-1$
beforeOrder(node.left);
beforeOrder(node.right);
}
/*
* 中序遍历
*/
public void inOrder(Node node){
if(node==null){
return;
}
inOrder(node.left);
System.out.print(node.value+Messages.getString("BinaryTree.2")); //$NON-NLS-1$
inOrder(node.right);
}
/*
* 后序遍历
*/
public void afterOrder(Node node) {
if(node==null) {
return;
}
afterOrder(node.left);
afterOrder(node.right);
System.out.print(node.value+Messages.getString("BinaryTree.3")); //$NON-NLS-1$
}
/*
* 查找
*/
public Node search(int value) {
if(root==null) {
return null;
}
Node index = root;
while (index!=null) {
if(index.value==value){
return index;
}else if(index.value>value) {
index = index.left;
}else {
index=index.right;
}
}
return null;
}
/**
* 找目标值的父节点
*/
public Node searchParent(int value) {
if(root==null) {
return null;
}
Node index = root;
while (index!=null) {
if((index.left!=null&&index.left.value==value)||(index.right!=null&&index.right.value==value)) {
return index;
}else if (index.value>value) {
index=index.left;
}else {
index = index.right;
}

}
return null;
}

/**
* 找树当中的最小值
*/
public int min(Node node) {
Node index = node;
while(index.left!=null) {
index=index.left;
}
return index.value;
}

/**
* 删除
*/
public void delete(int value){
if(root==null) {
System.out.println(Messages.getString("BinaryTree.4"));
return;
}
//找目标节点
Node target = search(value);
if(target==null) {
System.out.println(Messages.getString("BinaryTree.5"));
return;
}
//找目标节点的父节点
Node parent = searchParent(value);

//三种情况，分情况讨论
if(target.left==null&&target.right==null) {
//叶子节点
//没有父节点
if(parent==null) {
root=null;
return;
}
//有父节点
if(parent.left!=null&&parent.left.value==value) {
parent.left=null;
}else {
parent.right=null;
}

}else if(target.left!=null&&target.right!=null) {
//有两棵子树的节点
int minVal = min(target.right);
delete(minVal);
target.value = minVal;

}else {
//有一棵子树的节点
//没有父节点
if(parent==null) {
//目标节点有左子树还是右子树
if(target.left!=null) {
root = root.left;
}else {
root=root.right;
}
return;
}
//有父节点
//判断目标节点是父节点的左孩子还是右孩子
if(parent.left!=null&&parent.left.value==value) {
//左孩子
//目标节点有左子树还是右子树
if(target.left!=null) {
parent.left = target.left;
}else {
parent.left = target.right;
}

}else {
//右孩子
//目标节点有左子树还是右子树
if(target.left!=null) {
parent.right = target.left;
}else {
parent.right = target.right;
}
}
}
}
@Override
public String toString() {
return "BinaryTree [root=" + root + "]";
}

}