C# 检查某个点是否存在于圆扇区内(Check whether a point exists in circle sector or not)

我们有一个以原点 (0, 0) 为中心的圆。作为输入，我们给出了圆扇区的起始角度和圆扇区的大小（以百分比表示）。 

例子： 

输入：半径 = 8          起始角 = 0          百分比 = 12           x = 3 y = 4           输出：点 (3, 4) 位于圆          扇区内

输入：半径 = 12         起始角 = 45         百分比 = 25            x = 3 y = 4          输出：点 (3, 4) 不位于          圆扇区内

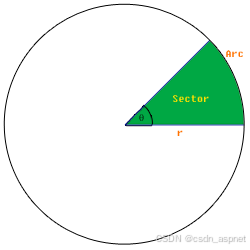
在此图像中，起始角度为 0 度，半径为 r，假设彩色区域百分比为 12%，则我们计算结束角度为360/百分比 + 起始角度。

为了确定点 (x, y) 是否存在于圆扇区（以原点为中心）内，我们需要找到该点的极坐标，然后执行以下步骤：

    1、使用这个将 x, y 转换为极坐标角度 = atan(y/x); 半径 = sqrt(x * x + y * y);

    2、那么角度必须介于 StartingAngle(起始角) 和 EndingAngle(终止角) 之间，并且半径必须介于 0 和您的半径之间。

示例代码：

// C# program to check if a point lies // inside a circle sector. using System.IO; using System;   class GFG {           static void checkPoint(int radius, int x, int y,                     float percent, float startAngle)     {                   // calculate endAngle         float endAngle = 360 / percent + startAngle;               // Calculate polar co-ordinates         float polarradius =                      (float)Math.Sqrt(x * x + y * y);                               float Angle = (float)Math.Atan(y / x);               // Check whether polarradius is less then          // radius of circle or not and Angle is          // between startAngle and endAngle or not         if (Angle >= startAngle && Angle <= endAngle                             && polarradius < radius)             Console.Write("Point ({0}, {1}) exist in "                          + "the circle sector", x, y);         else             Console.Write("Point ({0}, {1}) does not "                 + "exist in the circle sector", x, y);     }           // Driver code     public static void Main()     {         int radius = 8, x = 3, y = 4;         float percent = 12, startAngle = 0;         checkPoint(radius, x, y, percent, startAngle);     } }   // This code is contributed by Smitha Dinesh Semwal 

输出 ： 

点（3，4）位于圆扇区内

时间复杂度：  O(1)

辅助空间： O(1)

如果您喜欢此文章，请收藏、点赞、评论，谢谢，祝您快乐每一天。