目录
编辑
最短路径
Dijkstra算法(单源)
算法思想
算法步骤
代码实现
代码测试
缺点
Bellman-Ford算法(单源)
算法思想
算法步骤
代码实现
代码测试
Floyd-Warshall算法(多源)
算法思想
算法步骤
代码实现
代码测试
最短路径
最短路径问题:从在带权图的某一顶点出发,找出一条通往另一顶点的最短路径,最短也就是沿路径各边的权值总和达到最小。
Dijkstra算法(单源)
Dijkstra算法由荷兰计算机科学家Edsger W. Dijkstra在1956年提出,适用于含有非负权重的有向图或无向图。
算法思想
Dijkstra算法的基本思想是贪心算法。它维护一个距离数组,该数组记录了从源点到图中每个顶点的最短距离估计值。算法重复从未处理的顶点中选择具有最小距离估计值的顶点,并更新其邻居顶点的距离估计值,直到所有顶点都被处理。
算法步骤
1.初始化: 创建一个一维距离数组dist[],用于存储从源点到图中每个顶点的最短路径的估计距离。将所有顶点的距离初始化为无穷大(除了源点,其距离初始化为0)。 创建一个一维布尔数组visited[],用于记录顶点是否已被处理(即是否已经找到了从源点到该顶点的最短路径)。初始时,所有顶点都未被处理。 2.循环处理:
从未被标记处理的点连出去的所有边中选出距离最短的边,然后将该边的源节点u标记为处理过。 遍历顶点u的所有邻居顶点v,对于每个邻居顶点v,如果通过顶点u到达顶点v的距离(即dist[u] + matrix(u, v))小于当前记录的dist[v],则更新dist[v]为这个更小的值。 3.结束: 当所有顶点都被处理后,算法结束。此时,dist[]数组中存储的就是从源点到图中每个顶点的最短路径的长度。
为了记录下最短路径的整条路径是怎样的,使用一个一维数组pPath[]来标记每个点在最短路径中前一个节点是什么,这样就能够知道最短路径的整条路径是怎样的了(并查集思想)。
时间复杂度为O(n^2)。
图解:
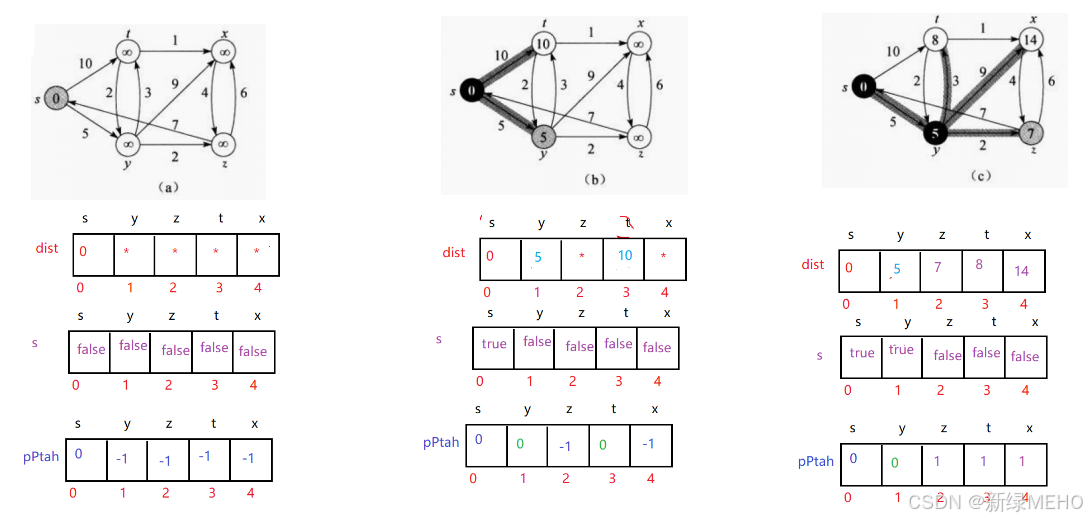
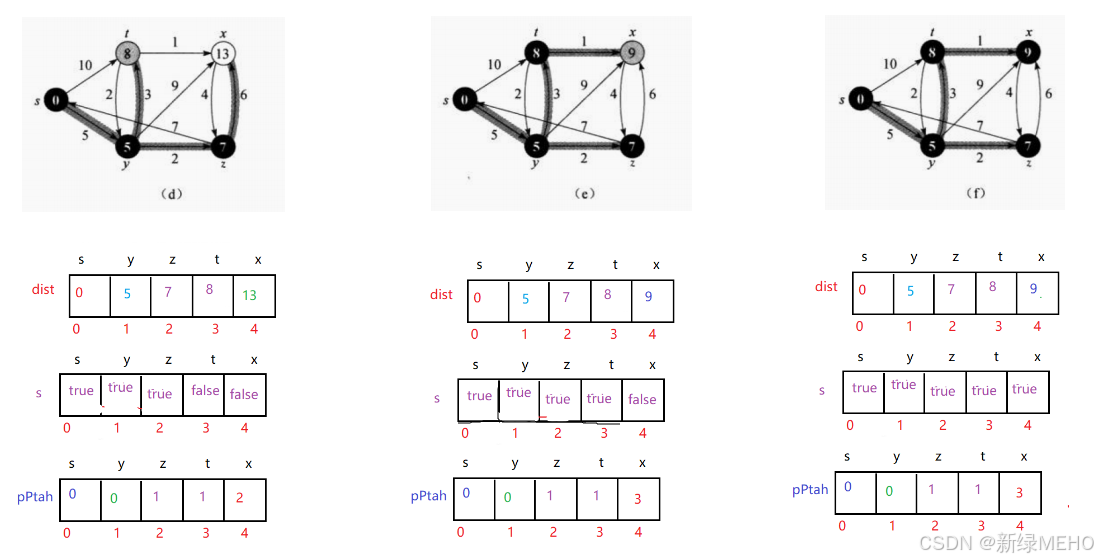
代码实现
Constant.java
public class Constant {
public static final int MAX = Integer.MAX_VALUE;
}
Dijkstra.java
public void dijkstra(char vSrc,int[] dist,int[] pPath) {
int srcIndex = getIndexOfV(vSrc);
//距离数据初始化
Arrays.fill(dist,Constant.MAX);
dist[srcIndex] = 0;
//路径数组初始化
Arrays.fill(pPath,-1);
pPath[srcIndex] = srcIndex;
//当前顶点是否被访问过
int n = arrayV.length;
boolean[] visted = new boolean[n];
//n个顶点,要更新n次,每次都要从0下标开始,找到一个最小值
for (int k = 0; k < n; k++) {
int min = Constant.MAX;
int u = srcIndex;
for (int i = 0; i < n; i++) {
if(visted[i] == false && dist[i] < min) {
min = dist[i];
u = i;//更新u下标
}
}
visted[u] = true;//u:s
//松弛u连接出去的所有的顶点 v
for (int v = 0; v < n; v++) {
if(visted[v] == false && matrix[u][v] != Constant.MAX
&& dist[u] + matrix[u][v] < dist[v]) {
dist[v] = dist[u] + matrix[u][v];
pPath[v] = u;//更新当前的路径
}
}
}
}
代码测试
public void printShortPath(char vSrc,int[] dist,int[] pPath) {
int srcIndex = getIndexOfV(vSrc);
int n = arrayV.length;
for (int i = 0; i < n; i++) {
//i下标正好是起点 则不进行路径的打印
if(i != srcIndex) {
ArrayList<Integer> path = new ArrayList<>();
int pathI = i;
while (pathI != srcIndex) {
path.add(pathI);
pathI = pPath[pathI];
}
path.add(srcIndex);
Collections.reverse(path);
for (int pos : path) {
System.out.print(arrayV[pos]+" -> ");
}
System.out.println(dist[i]);
}
}
}
public static void testGraphDijkstra() {
String str = "syztx";
char[] array = str.toCharArray();
GraphByMatrix g = new GraphByMatrix(str.length(),true);
g.initArrayV(array);
g.addEdge('s', 't', 10);
g.addEdge('s', 'y', 5);
g.addEdge('y', 't', 3);
g.addEdge('y', 'x', 9);
g.addEdge('y', 'z', 2);
g.addEdge('z', 's', 7);
g.addEdge('z', 'x', 6);
g.addEdge('t', 'y', 2);
g.addEdge('t', 'x', 1);
g.addEdge('x', 'z', 4);
int[] dist = new int[array.length];
int[] parentPath = new int[array.length];
g.dijkstra('s', dist, parentPath);
g.printShortPath('s', dist, parentPath);
}
运行结果:

缺点
无法解决边权为负的最短路径。
例如:
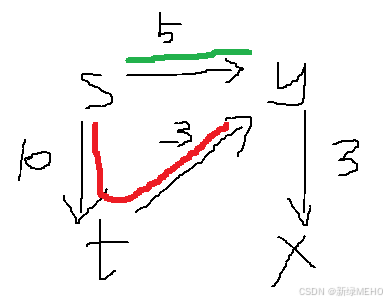
对于上面的情况,我们知道,Dijkstra算法一定会选择“绿色”的那条路,但是“红色”的那条路是最短的,这就是Dijkstra算法无法解决的边权为负的情况,为了解决这个问题,可以使用下面的Bellman-Ford算法。
Bellman-Ford算法(单源)
Bellman-Ford算法由理查德·贝尔曼和莱斯特·福特共同创立。该算法特别适用于图中存在负权边的情况,这是其相对于其他算法(如Dijkstra算法)的主要优势。
算法思想
Bellman-Ford算法通过多次迭代来逐步逼近最短路径的真实值。在每次迭代中,算法会尝试通过所有边来更新起点到其他所有点的最短距离。如果图中不存在负权回路,那么经过有限次迭代后,算法将收敛到正确的最短路径解。
算法步骤
1.初始化距离数组dist[],将起点到自身的距离设为0,起点到其他所有点的距离设为无穷大。 2.执行n次迭代(n为图中顶点的数量),每次迭代都对所有边执行松弛操作。 3.在第n+1次迭代中,再次对所有边执行松弛操作,但这次是为了检测图中是否存在负权回路。如果还能更新某些点的距离,则说明图中存在负权回路。
为了记录下最短路径的整条路径是怎样的,使用一个一维数组pPath[]来标记每个点在最短路径中前一个节点是什么,这样就能够知道最短路径的整条路径是怎样的了(并查集思想)。
时间复杂度较高,为O(n^3),不适合处理大规模图。
图解:
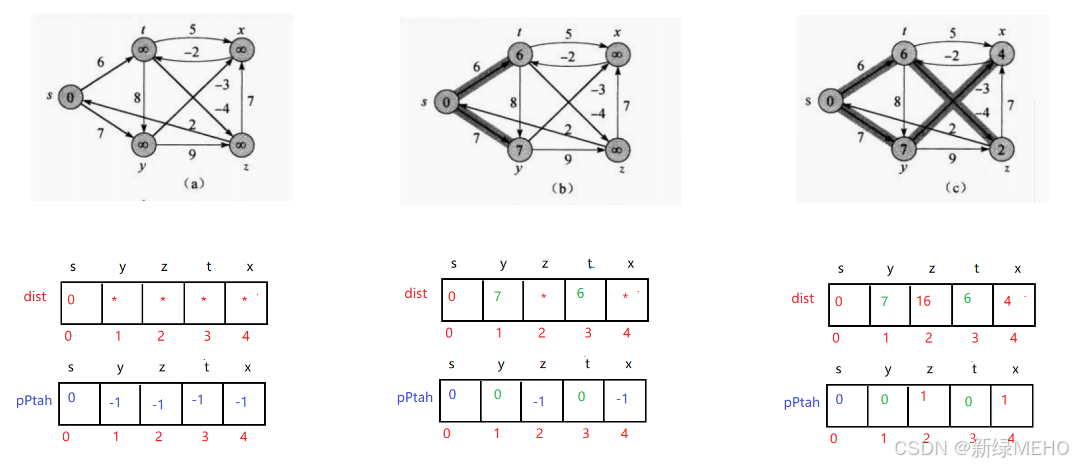
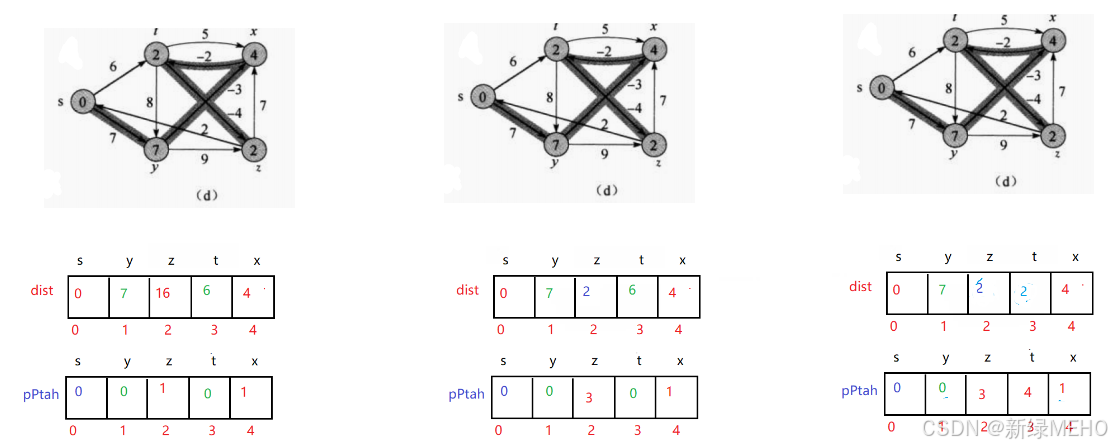
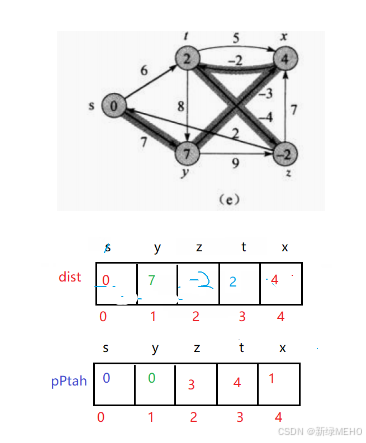
代码实现
public boolean bellmanFord(char vSrc,int[] dist,int[] pPath) {
int srcIndex = getIndexOfV(vSrc);
//距离数据初始化
Arrays.fill(dist,Constant.MAX);
dist[srcIndex] = 0;
//路径数组初始化
Arrays.fill(pPath,-1);
pPath[srcIndex] = 0;
int n = arrayV.length;
for (int k = 0; k < n; k++) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if(matrix[i][j] != Constant.MAX &&
dist[i] + matrix[i][j] < dist[j]) {
dist[j] = dist[i] + matrix[i][j];
pPath[j] = i;
}
}
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if(matrix[i][j] != Constant.MAX &&
dist[i] + matrix[i][j] < dist[j]) {
return false;
}
}
}
return true;
}
代码测试
不带负权回路的情况
public static void testGraphBellmanFord() {
String str = "syztx";
char[] array = str.toCharArray();
GraphByMatrix g = new GraphByMatrix(str.length(),true);
g.initArrayV(array);
g.addEdge('s', 't', 6);
g.addEdge('s', 'y', 7);
g.addEdge('y', 'z', 9);
g.addEdge('y', 'x', -3);
g.addEdge('z', 's', 2);
g.addEdge('z', 'x', 7);
g.addEdge('t', 'x', 5);
g.addEdge('t', 'y', 8);
g.addEdge('t', 'z', -4);
g.addEdge('x', 't', -2);
int[] dist = new int[array.length];
int[] parentPath = new int[array.length];
boolean flg = g.bellmanFord('s', dist, parentPath);
if(flg) {
g.printShortPath('s', dist, parentPath);
}else {
System.out.println("存在负权回路");
}
}
运行结果:
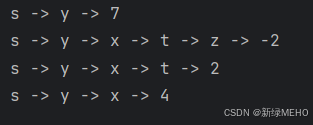
带负权回路的情况
public static void testGraphBellmanFord() {
String str = "syztx";
char[] array = str.toCharArray();
GraphByMatrix g = new GraphByMatrix(str.length(),true);
g.initArrayV(array);
//负权回路实例
g.addEdge('s', 't', 6);
g.addEdge('s', 'y', 7);
g.addEdge('y', 'z', 9);
g.addEdge('y', 'x', -3);
g.addEdge('y', 's', 1);
g.addEdge('z', 's', 2);
g.addEdge('z', 'x', 7);
g.addEdge('t', 'x', 5);
g.addEdge('t', 'y', -8);
g.addEdge('t', 'z', -4);
g.addEdge('x', 't', -2);
int[] dist = new int[array.length];
int[] parentPath = new int[array.length];
boolean flg = g.bellmanFord('s', dist, parentPath);
if(flg) {
g.printShortPath('s', dist, parentPath);
}else {
System.out.println("存在负权回路");
}
}
运行结果:
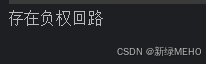
Floyd-Warshall算法(多源)
算法思想
Floyd-Warshall算法采用动态规划的思想,通过三重循环遍历图中的每个顶点,并尝试将其作为中间点来更新任意两个顶点之间的最短路径。算法的核心在于不断比较和更新路径长度,直到找到所有顶点对之间的最短路径。
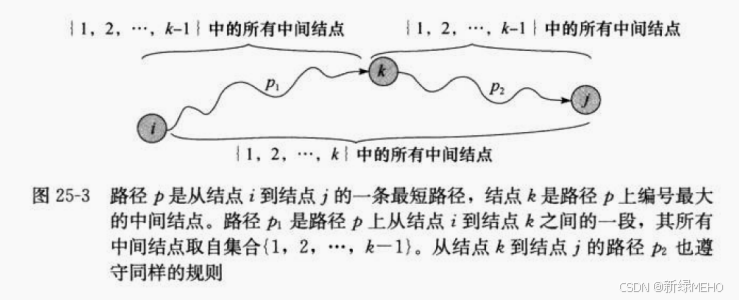

算法步骤
1.初始化: 使用图的带权邻接矩阵A作为起点,其中A[i][j]表示顶点i到顶点j的直接距离。如果i和j之间没有直接连接,则A[i][j]被设置为无穷大(或一个足够大的数)。 2.三重循环: 外层循环遍历所有可能的中间点k(1到n)。 中间两层循环分别遍历所有起点i和终点j(1到n)。 在每次迭代中,检查是否可以通过顶点k来缩短从i到j的路径长度。如果可以,则更新A[i][j]为A[i][k] + A[k][j]。 3.结束: 当所有顶点都被用作中间点时,算法结束。此时,A矩阵中的每个元素A[i][j]都表示从顶点i到顶点j的最短路径长度。
为了记录下最短路径的整条路径是怎样的,使用一个二维数组pPath[]来标记每个点在最短路径中前一个节点是什么,这样就能够知道最短路径的整条路径是怎样的了(并查集思想)。
时间复杂度较高,为O(n^3),不适合处理大规模图。
代码实现
public void floydWarShall(int[][] dist,int[][] pPath) {
int n = arrayV.length;
for (int i = 0; i < n; i++) {
Arrays.fill(dist[i],Constant.MAX);
Arrays.fill(pPath[i],-1);
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if(matrix[i][j] != Constant.MAX) {
dist[i][j] = matrix[i][j];
pPath[i][j] = i;
}else {
pPath[i][j] = -1;
}
if(i == j) {
dist[i][j] = 0;
pPath[i][j] = -1;
}
}
}
for (int k = 0; k < n; k++) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if(dist[i][k] != Constant.MAX &&
dist[k][j] != Constant.MAX &&
dist[i][k] + dist[k][j] < dist[i][j]) {
dist[i][j] = dist[i][k] + dist[k][j];
//更新父节点下标
//pPath[i][j] = k;//不对
//如果经过了 i->k k->j 此时是k
//i->x->s->k k->..t->…x->j
pPath[i][j] = pPath[k][j];
}
}
}
// 测试 打印权值和路径矩阵观察数据
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if(dist[i][j] == Constant.MAX) {
System.out.print(" * ");
}else{
System.out.print(dist[i][j]+" ");
}
}
System.out.println();
}
System.out.println("=========打印路径==========");
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
System.out.print(pPath[i][j]+" ");
}
System.out.println();
}
System.out.println("=================");
}
}
代码测试
public static void testGraphFloydWarShall() {
String str = "12345";
char[] array = str.toCharArray();
GraphByMatrix g = new GraphByMatrix(str.length(),true);
g.initArrayV(array);
g.addEdge('1', '2', 3);
g.addEdge('1', '3', 8);
g.addEdge('1', '5', -4);
g.addEdge('2', '4', 1);
g.addEdge('2', '5', 7);
g.addEdge('3', '2', 4);
g.addEdge('4', '1', 2);
g.addEdge('4', '3', -5);
g.addEdge('5', '4', 6);
int[][] dist = new int[array.length][array.length];
int[][] parentPath = new int[array.length][array.length];
g.floydWarShall(dist,parentPath);
for (int i = 0; i < array.length; i++) {
g.printShortPath(array[i],dist[i],parentPath[i]);
System.out.println("************************");
}
}
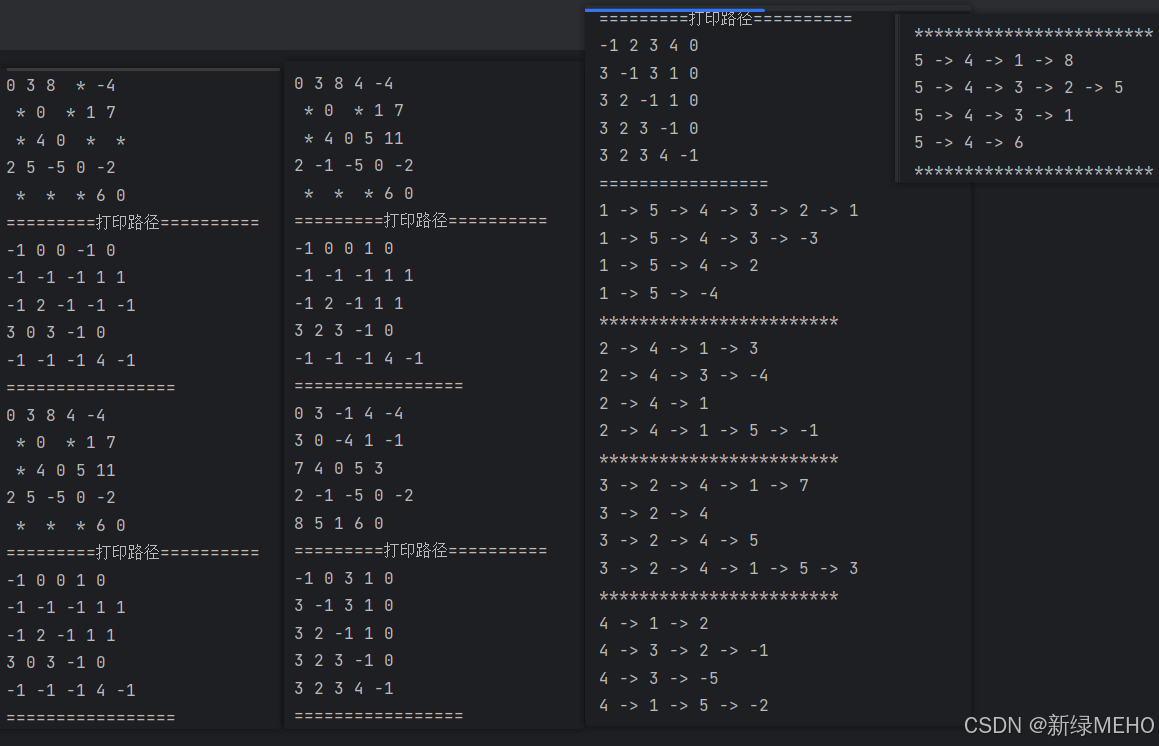
运行结果:
 网硕互联帮助中心
网硕互联帮助中心


评论前必须登录!
注册