词法分析(3)：从正则文法到状态转移表

本文是本人撰写的编译原理讲义。

本系列讲义适用于：被强迫学习编译原理前端，或者希望弄明白如何做科研的人

蛮力之路：灵肉纠缠

上一节，我们讲到了词法分析程序的大厦已经基本落成，躲在乌云后面的雷公一直在找机会劈死那些只知道用理论来装AC娘但不知道如何落地的人。

那还是先使出一招见微知著，从我们的老朋友f开始观察

S->aA

A->cC | b

C->cA

假定我们就是那台识别的机器，我们现在一手拿着规则，一手拿着用户输入的代码。

然后我们操作一个光标，从0号位置不停向后一个一个符号读取代码。那接下来的过程，就是根据当前光标表示的符号，处理一下当前的状态，光标右移，不断循环。

以f的第二条规则为例，你现在需要判断即将看到的符号到底是b还是c从而做出对应的操作。

很容易编码成如下结构

// 初始化当前状态为起始状态 S
CurrentState = S;

// 循环控制变量，用于在识别成功（到达接收状态）后优雅地退出循环
loop = true;

// 这是状态机的“驱动引擎”。只要还未识别成功或出错，就持续运行。
while(loop){
// 根据当前所处的状态，决定下一步的行为。
switch (CurrentState){
// 状态S：起始状态 (Start State)
case 'S':
// 等待接收第一个字符，根据规则，它必须是 'c'。
ch = getchar(); // 读取一个新字符
if (ch == 'a')
CurrentState = 'A'; // 如果是 'a'，成功迈出第一步，状态转移到 A
else
CurrentState = '!'; // 如果不是，进入错误状态。
break;

// 状态A：已接收到偶数个 'c' (例如：空, cc, cccc…)
case 'A':
// 在此状态下，我们期望看到两种可能：
// 1. 接收到结束符 'b'，从而成功完成匹配。
// 2. 接收到下一个 'c'，使得 'c' 的总数变为奇数。
ch = getchar();
switch(ch){
case 'c':
CurrentState = 'C'; // 接收到一个 'c' (总数为偶数)，状态转移到 C
break;
case 'b': // 接收到结束符 'b'，这是一个“接收”动作 (Accept)
loop = false; // 成功识别！设置循环为false，准备退出。
break;
default:
CurrentState = '!'; // 如果不是，进入错误状态。
}
break;

// 状态C：已接收到奇数个 'c' (例如：c, ccc, ccccc…)
case 'C':
// 在此状态下，根据规则，我们必须再次看到一个 'c'，
// 才能让 'c' 的总数变回偶数，从而回到状态 A。
ch = getchar();
if (ch == 'c')
CurrentState = 'A'; // 接收到又一个 'c' (总数为偶数)，状态转移回 A
else
CurrentState = '!'; // 如果不是，进入错误状态。
break;

// 默认情况：用于捕捉任何意外的或未定义的状态。
default:
case '！':
error(); // 处理出错情况
}
}

槽点过多都有点让人不知道从哪里开始。

首先，这里读一个符号就要getchar一下，那对于前面的S->abc岂不是要getchar 3次？

其次，中间每一个状态开始之后也都要getchar一下，重复严重。

再者，对于我们之前随手写下S->A | B，由于没有符号让它可以进行判断，我们要如何处理呢？

最后一点，我们前面好不容易从屎山代码里面逃出来，现在这不就是又一坨大的吗？每次新增一条规则，就得改写代码，最后让逻辑变得又长又臭。

优雅之道：抽象飞升

试想一下，如果我们的规则可以写在一个配置表上，然后只通过一个莫得感情的执行机器自动去执行，那肯定要比直接改代码要来得舒服。

换而言之，我们需要把上面这段代码中，把内在真正的逻辑，以及真正要做的动作进行分开。

代码终究只是文字，而文字是对现象的某种抽象。但是，如果抽象的方式错误可能会让我们反而看不清事实。因此，看着满屏代码不知如何抽象的时候，我会考虑把它原本的样子还原出来，也就是画出不同状态之间的变化地图。

还原的逻辑非常简单：从哪个状态出来，在遇到什么符号之后会跳到什么新状态，把他们全部连在一起。

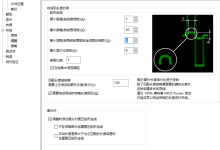
啪的一声，很快啊：

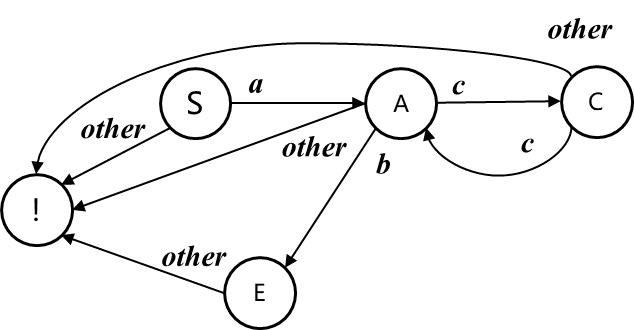
其中不同的圈圈分别表示：

! 错误状态, 铁定不会认可输入串

S 初始状态, 观望

A 读一个a, 观望

E 读一个b, 识别出了目标串 //也就是说，对于A->b这样的无后产生式，改写成A->bE；E->ε两个产生式，其中E就是新增以表示终态的辅助状态

C 读一个c, 观望

注意到，这个图并不能独立于注释存在，因为有一些关键还藏在文字中。

比如，这个指引地图的出发位置在哪里？终点在哪里？这些信息全都用文字描述，因此显得非常冗余。

因此，我们可以用双箭头指向特定状态表示开始，用双圈装饰合法的结束状态，从而把这一切都通过特殊标记在图上表示出来。最后通过把错误处理状态隐去，就可以得到如下的状态跳转地图：

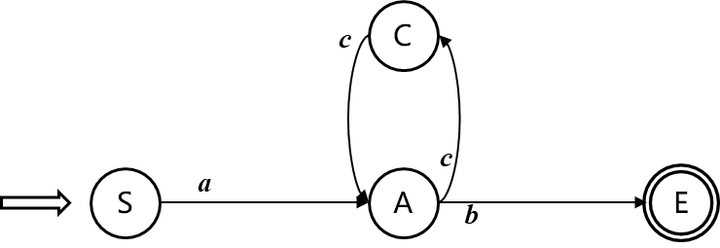
这图对人是清晰易懂了，但还没有解锁多模态理解能力机器表示：“看不懂啊！！”

那么，有没有一种方法，可以让机器无偏理解这么一个图？

那就是数据结构中的图；那就是离散数学中的图论；那就是计算机组成原理中的状态机。

在这些课程中，我们都反复学到过一种叫做邻接矩阵的东西，其中第x行y列元素的值，表示了从点x到点y是否存在路径，如果存在则1，如果没有则为0。

对有向图进行编程的时候，我们不需要每遇到一个新图就进行一次全新的复杂编码，而只需要把有向图的连接关系用矩阵表示出来，就可以让计算机进行一系列求解。

而我们现在要解决的问题是，看看在输入特定的符号串之后，是否可以到达一个合法的终态。如果可以就说明这个词被识别出来，否则就是出错。

那如果，我们在邻接矩阵元素只标记为0/1的基础上，把记号改为具体的实义符号，那对于有值的格子，它的意义就变成了“点x在遇到什么符号后会跳转到点y”。

但这个表述和我们实际上要解决的问题还是有差距，我们更多是想要知道“点x在遇到某个符号后会跳转到哪个点”

由此，我们把上图对应的邻接矩阵

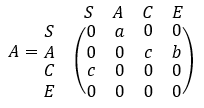
进行变换后，就可以得到如下表格：

当前状态

a

b

c

是否终态

S

A

C

E

恭喜你，得到了状态转移表

注意，在这个表格中，最后一列用来指示这个状态是否为终态，和前面的激励列含义完全不同。因此这里实际上是合并了两个表格。在实际实现中可以用两个数组分别保存对应的信息。

之后的词法编辑器中，你只需要：1. 把规则转化成对应的状态转移表；2.再把状态转移表输入到程序中；3.在程序中输入待识别的代码符号串；4.由程序根据状态转移表实现机械画的单词识别。

说了那么多，那个莫得感情的执行程序呢？

// 初始化
//假定已经有TransitionTable二维数组用以保存状态转移表
//另有FinalState布尔数组用于保存对应状态是否为终态
CurrentState = 'S'; // 从起始状态开始
// 循环读取字符，直到文件结束
while ( ch = getchar() ) {
// 核心：查表，更新状态！
CurrentState = TransitionTable[CurrentState][ch];
// 检查是否进入特殊状态
if (CurrentState == '!') {
// 处理错误…
break;
}
if (FinalState[CurrentState] == true) {
// 成功！识别出一个单词！
// 返回 Token，准备下一次识别…
}
}

这种抽象就好比，你的身体只是在执行你大脑中的指示，你的硬件只是在执行软件指令。

而不用像八音盒中的音乐程序一样，完全固化在硬件中，自出厂之日就无法变化。

“血肉苦弱，机械飞升”讲的是肉体的脆弱，但难道机械的硬件就不会老化么？

当你懂得抽象的时候，你的灵魂就已经挣脱了硬件的束缚，以数字形式永存于世了。

硬件苦弱，抽象飞升

器有所缚，道以无穷

形骸易朽，逻辑不灭

小结

本节介绍了一个很简单的例子用来说明如何对正则语法进行编码，从而避免屎山代码对人的填埋。

但这并不是终点。我们尚未能完全解决任意正则语法到状态转移表的转换，也未能很优雅地解决状态转移表的使用问题。

欲知如何处理，且听下回分解。