常用的降噪与PCA技术

1. 常用的降噪方法

        降噪是去除信号或数据中噪声的过程，常见方法可分为信号处理、统计学习、深度学习等类别，具体如下：

1.1 滤波法（信号处理领域）

        – 均值滤波：用滑动窗口内像素的平均值替代中心像素，平滑噪声（适用于高斯噪声）。

        – 中值滤波：用滑动窗口内像素的中值替代中心像素，有效去除椒盐噪声。

        – 高斯滤波：通过高斯核卷积平滑信号，保留边缘的同时抑制高频噪声。

        – 小波降噪：利用小波变换分解信号与噪声，通过阈值处理去除噪声分量，适用于非平稳信号。

1.2 统计方法

– 基于模型的降噪：如假设信号服从某种分布（高斯混合模型），通过参数估计分离信号与噪声。

– 贝叶斯降噪：结合先验知识和观测数据，通过后验概率估计最优信号。

1.3 深度学习方法

        – 自编码器：通过编码-解码结构学习信号的潜在表示，忽略噪声成分。

        – U-Net及变体：在图像降噪中广泛应用，通过跳跃连接保留细节的同时去除噪声。

        – 生成对抗网络（GAN）：通过生成器和判别器的对抗训练，生成去噪后的信号。

        – 其他方法：

                – 奇异值分解（SVD）：对数据矩阵进行SVD分解，保留主要奇异值（对应信号），舍弃小奇异值（对应噪声）。

                – 非局部均值降噪：利用图像中重复的相似结构，通过加权平均去除噪声（适用于图像）。

​​降噪与降维的关系​​：

• 降维是保留主成分
• 降噪是舍弃次要成分（通常含噪声）

2. 主成分分析（PCA）

        主成分分析是一种无监督的降维方法，核心是通过线性变换将高维数据映射到低维空间，同时保留数据中最主要的信息（方差最大的方向）。

2.1 核心思想

        高维数据中存在冗余（特征间相关），PCA通过寻找一组正交的“主成分”（新特征），使数据在主成分上的投影方差最大，用较少的主成分保留原数据的大部分信息。

2.2 步骤

        1. 数据标准化：对原始数据进行中心化（减去均值），使各特征均值为0（若特征量纲不同，需先标准化，如除以标准差）。

        2. 计算协方差矩阵：描述特征间的相关性。

        3. 求解协方差矩阵的特征值和特征向量：特征值表示对应特征向量方向上的方差大小，特征向量为数据投影的方向（主成分）。

        4. 选择主成分：按特征值从大到小排序，选取前k个特征向量（累计方差贡献率通常≥85%），构成投影矩阵。

        5. 数据降维：将原始数据与投影矩阵相乘，得到k维的低维数据。

2.3 应用

        数据可视化（将高维数据降为2D/3D）、去除噪声（保留主要方差，过滤小方差的噪声）、加速模型训练（减少特征维度）。

3. PCA技术补充

3.1数学本质

        PCA是一种线性降维方法，其目标是最大化低维数据的方差（即保留数据的主要变异信息），等价于最小化原始数据与低维投影的重构误差（均方误差）。

3.2 优缺点

        – 优点：计算简单、无参数依赖、可去除特征间的冗余和噪声。

        – 缺点：仅能捕捉线性关系，对非线性数据降维效果差；主成分的物理意义不明确（难以解释）；对异常值敏感。

3.3 扩展

        针对非线性数据，可采用核PCA（通过核函数将数据映射到高维空间，再进行PCA降维）；针对高维稀疏数据，可采用稀疏PCA（使主成分具有稀疏性，便于解释）。

3.4 代码示例

        通过PCA找到数据的主要变化方向，保留重要信息（信号）的同时，舍弃次要方向（通常为噪声），实现数据降维与降噪的协同处理。

        线性变换 → 协方差矩阵分解 → 投影到最大方差方向 → 丢弃噪声主导的小方差成分

import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler

# 1. 生成带噪声的二维数据 ======================================
np.random.seed(42)
n_samples = 300
true_mean = [3, 2] # 真实数据的均值
cov = [[1, 0.8], [0.8, 1]] # 协方差矩阵（存在相关性）

# 生成真实信号（线性相关的二维数据）
X_true = np.random.multivariate_normal(true_mean, cov, n_samples)

# 添加高斯噪声（模拟观测噪声）
noise = np.random.normal(0, 0.6, size=(n_samples, 2))
X_noisy = X_true + noise # 含噪声的观测数据

# 2. 数据标准化 ==============================================
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X_noisy) # 标准化（均值为0，方差为1）

# 3. PCA降维与重建 ==========================================
pca = PCA(n_components=1) # 降到1维（为了清晰展示降噪效果）
X_pca = pca.fit_transform(X_scaled) # 降维后的数据
X_reconstructed = pca.inverse_transform(X_pca) # 重建回原始空间

# 4. 可视化结果 ==============================================
plt.figure(figsize=(15, 5))

# 4.1 原始数据与噪声数据对比
plt.subplot(131)
plt.scatter(X_true[:, 0], X_true[:, 1], c='blue', alpha=0.6, label='真实信号')
plt.scatter(X_noisy[:, 0], X_noisy[:, 1], c='red', alpha=0.2, label='含噪观测')
plt.title('数据分布对比')
plt.xlabel('特征1')
plt.ylabel('特征2')
plt.legend()
plt.grid(True)

# 4.2 主成分方向可视化
plt.subplot(132)
# 绘制主成分方向
pc_direction = pca.components_[0] # 第一主成分方向向量
plt.arrow(0, 0, pc_direction[0], pc_direction[1],
head_width=0.3, head_length=0.3, fc='black', ec='black')
plt.text(pc_direction[0]*1.2, pc_direction[1]*1.2,
'主成分方向', fontsize=12)

# 绘制数据点
plt.scatter(X_scaled[:, 0], X_scaled[:, 1], c='gray', alpha=0.4)
plt.title('主成分方向分析')
plt.xlabel('标准化特征1')
plt.ylabel('标准化特征2')
plt.axis('equal')
plt.grid(True)

# 4.3 PCA降噪效果对比
plt.subplot(133)
plt.scatter(X_noisy[:, 0], X_noisy[:, 1], c='red', alpha=0.2, label='含噪数据')
plt.scatter(X_reconstructed[:, 0], X_reconstructed[:, 1],
c='green', alpha=0.6, label='PCA降噪')
plt.title('PCA降噪效果')
plt.xlabel('特征1')
plt.ylabel('特征2')
plt.legend()
plt.grid(True)

plt.tight_layout()

# 5. 解释方差分析 ==========================================
print(f"主成分解释方差比例: {pca.explained_variance_ratio_[0]:.2%}")
plt.show()

主成分解释方差比例: 78.20%

表示该主成分方向携带了原始数据78.20%的方差信息（噪声通常对应剩余的小部分方差）

工程意义​​：

•量化降维过程中的信息保留程度

•指导选择主成分数量（如累计方差>78%）

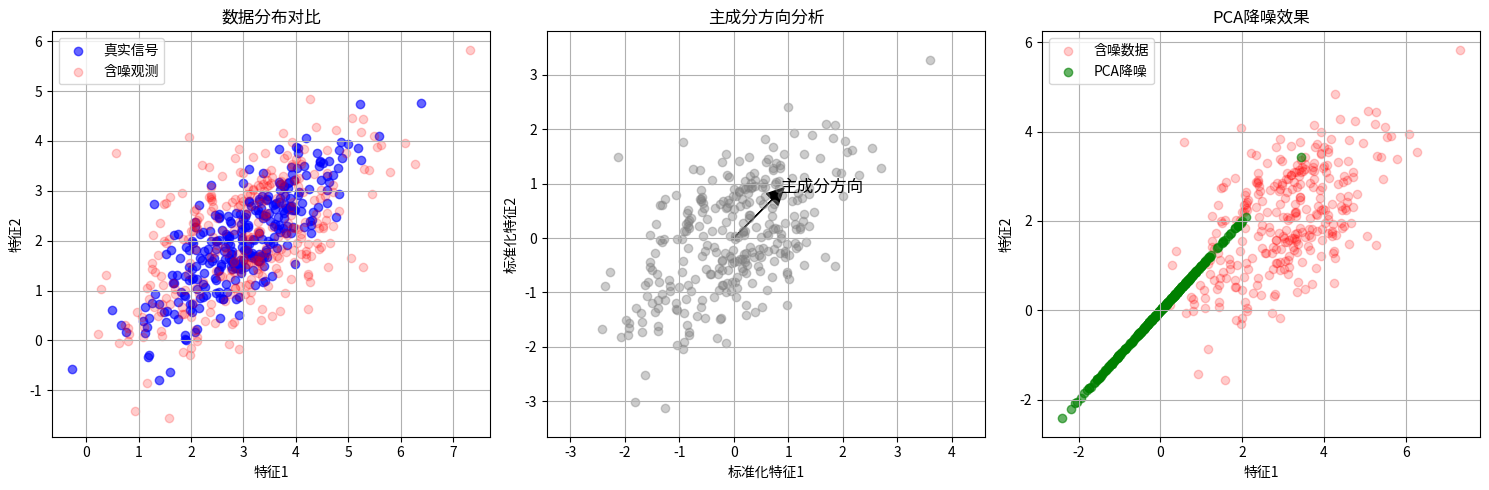
图1：数据分布对比

        蓝色点​​：原始真实信号（呈现明显的线性相关分布）

        红色点​​：添加噪声后的观测数据（在原始信号周围随机散布）

        直观展示噪声如何破坏原始数据的结构特征

图2：主成分方向分析

        ​​黑色箭头​​：PCA自动发现的第一主成分方向（数据方差最大的方向）

        灰色点为标准化后的数据，箭头方向与数据分布的主要趋势一致

        说明PCA能自动捕捉数据的主要变异方向

图3：PCA降噪效果

        ​​红色点​​：原始含噪数据（散布范围大）

        ​​绿色点​​：PCA降噪结果（全部投影到主成分方向后重建）

        可以看到：

        噪声被有效抑制（点更集中）

        保留了原始数据的线性趋势

        重建数据完全落在主成分方向上（实现降维+降噪）

总结

1.降噪本质​​：通过保留主要方差方向（信号），舍弃次要方向（通常含噪声）

2.​​标准化必要性​​：确保不同特征具有可比性，避免量纲影响主成分方向

3.​​线性假设​​：PCA只适合处理线性关系的数据（非线性数据需用核PCA）

4.​​维度选择​​：通过解释方差比例决定保留多少主成分（本例选择保留85%以上信息）