MATLIB学习文档（四）

目录

4.3 MATLAB中的矩阵

4.4.1 矩阵的创建方法

直接输入法

语法规则

代码示例

关键点

内置函数创建法

全零矩阵 (zeros)

全一矩阵 (ones)

单位矩阵 (eye)

随机矩阵

标量填充矩阵 (fill / 标量扩展)

矩阵拼接法

水平拼接

垂直拼接

注意事项

colon 运算符与 linspace 函数

colon 运算符 (:)

linspace 函数

关键点对比

特殊矩阵

对角矩阵 (diag)

分块对角矩阵（blkdiag）

魔方矩阵 (magic)

希尔伯特矩阵 (hilb)

从文本文件加载矩阵

Load

Dlmread

Textscan

从 Excel 文件加载

Xlsread

Readmatrix

4.4.2 矩阵元素的引用

位置索引

1. 单个元素引用

2. 多个元素引用

3. 冒号运算符

逻辑索引

1. 生成逻辑索引

2. 直接逻辑索引

线性索引

1. 单个线性索引

2. 线性索引与位置索引的转换

注意事项

混合索引

总结

4.4.3 矩阵元素的修改和删除

矩阵元素的修改

 1. 修改单个元素

2. 修改多个元素（批量修改）

矩阵元素的删除

1. 删除行

2. 删除列

3. 删除满足特定条件的行（高级技巧）

注意事项

总结

4.4.4 矩阵的拼接和重复

矩阵的拼接

1. 水平拼接

2. 垂直拼接

3. 多维矩阵的拼接

矩阵的重复

1. repmat 函数

2. kron 函数

repmat VS kron：

3. 利用索引进行重复（高级技巧）

总结

4.4.5 矩阵的重构和重新排列

矩阵的重构

1. reshape – 核心重构函数

2. permute – 维度置换

3. squeeze – 移除单一维度

4. shiftdim – 维度循环移位

矩阵的重新排列

1. 转置 ' 和 .'

2. flip 系列函数 – 翻转

3. rot90 – 旋转

4. sort 和 sortrows – 排序

总结

4.3 MATLAB中的矩阵

4.4.1 矩阵的创建方法

直接输入法

这是最简单直接的方式，适用于创建小型、元素已知的矩阵。

语法规则

矩阵元素用方括号 [ ] 括起来。

同一行内的元素用空格或逗号 , 分隔。

不同行之间用分号 ; 或者回车键分隔。

代码示例

% 创建一个 2×3 的矩阵 A

% 方法一：使用空格和分号

A = [1 2 3; 4 5 6]

% 方法二：使用逗号和分号（效果相同）

B = [1, 2, 3; 4, 5, 6]

% 创建一个行向量 (1×4 矩阵)

row_vector = [10 20 30 40]

% 创建一个列向量 (3×1 矩阵)

col_vector = [100; 200; 300]

% 创建一个标量 (1×1 矩阵)

scalar = 42

关键点

在直接输入时，必须确保每一行的元素数量相同，否则 MATLAB 会报错。

对于大型矩阵，直接输入法容易出错且可读性差，应优先考虑其他方法。

内置函数创建法

MATLAB 提供了大量内置函数，用于快速生成具有特定属性的矩阵，这在编程和算法实现中极为常用。

全零矩阵 (zeros)

创建所有元素均为 0 的矩阵。

% 创建一个 3×4 的全零矩阵

Z1 = zeros(3, 4);

% 创建一个与矩阵 A 大小相同的全零矩阵

A = [1 2; 3 4];

Z2 = zeros(size(A)); % 非常实用，用于初始化

全一矩阵 (ones)

创建所有元素均为 1 的矩阵。

% 创建一个 2×5 的全一矩阵

O1 = ones(2, 5);

% 创建一个与向量 v 大小相同的全一行向量

v = [1, 2, 3];

O2 = ones(size(v));

单位矩阵 (eye)

创建主对角线为 1，其余为 0 的方阵。

% 创建一个 4×4 的单位矩阵

I1 = eye(4);

% eye(m, n) 可以创建 m x n 的非方阵，主对角线为 1

I2 = eye(3, 5);

随机矩阵

均匀分布随机矩阵 (rand)

生成一个矩阵，其元素在 (0, 1) 区间内均匀分布。

% 创建一个 5×5 的均匀分布随机矩阵

R1 = rand(5);

% 创建一个 2×3 的均匀分布随机矩阵

R2 = rand(2, 3);

标准正态分布随机矩阵 (randn)

生成一个矩阵，其元素服从均值为 0，标准差为 1 的标准正态分布。

% 创建一个 1000×1 的标准正态分布随机向量（常用于模拟）

N1 = randn(1000, 1);

% 创建一个 3×3 的标准正态分布随机矩阵

N2 = randn(3);

随机整数矩阵 (randi)

生成一个矩阵，其元素为指定范围内的均匀分布的随机整数。

% 生成一个 2×4 的矩阵，元素为 1 到 10 之间的随机整数

RI1 = randi(10, 2, 4);

%开头是1可以省略randi([1,10],2,4)与RI1 = randi(10, 2, 4)一致

% 生成一个 3×3 的矩阵，元素为 -5 到 5 之间的随机整数

RI2 = randi([-5, 5], 3);

标量填充矩阵 (fill / 标量扩展)

虽然 fill 不是标准函数名，但 MATLAB 的标量扩展功能可以轻松实现。将一个标量与一个全一矩阵相乘即可。

% 创建一个 3×3 的，所有元素都是 7 的矩阵

val = 7;

rows = 3;

cols = 3;

F = val * ones(rows, cols);

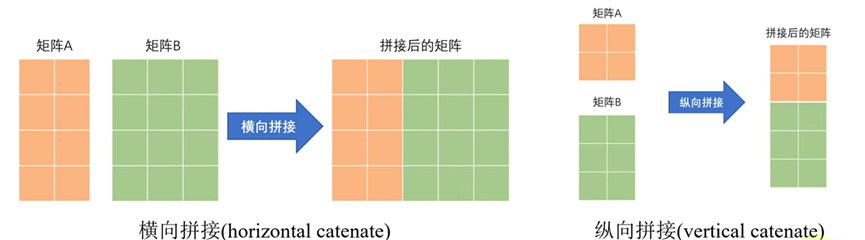
矩阵拼接法

通过将已有的矩阵（或向量）水平或垂直地连接起来，形成新的、更大的矩阵。

水平拼接

使用空格或逗号 , 作为分隔符。

注意：要求所有参与拼接的矩阵行数必须相同。

A = [1 2; 3 4];

B = [5 6; 7 8];

% 水平拼接 A 和 B

C_horiz = [A, B]  % 或 C_horiz = [A B]

% 结果:

% C_horiz =

%      1     2     5     6

%      3     4     7     8

垂直拼接

使用分号 ; 或者输入回车键作为分隔符。

注意，要求所有参与拼接的矩阵列数必须相同。

A = [1 2; 3 4];

D = [9 10; 11 12];

% 垂直拼接 A 和 D

C_vert = [A; D]

% 结果:

% C_vert =

%      1     2

%      3     4

%      9    10

%     11    12

注意事项

拼接时，必须严格遵守“水平拼接行数相同，垂直拼接列数相同”的规则，否则会报 "Dimensions of arrays being concatenated are not consistent" 错误。

MATLAB 还提供了 cat 函数，可以指定沿哪个维度进行拼接，horzcat (水平拼接) 和 vertcat (垂直拼接) 是其特例。

% 使用 cat 函数进行拼接

% dim=1 表示垂直拼接，dim=2 表示水平拼接

C_cat1 = cat(1, A, D); % 等同于 [A; D]

C_cat2 = cat(2, A, B); % 等同于 [A, B]

colon 运算符与 linspace 函数

这两种方法主要用于创建等差序列向量，是创建规律矩阵的基础。

colon 运算符 (:)

这是 MATLAB 中最强大和常用的运算符之一。

语法 1: start:end

创建从 start 到 end，步长为 1 的行向量。

v1 = 1:5  % 结果: [1 2 3 4 5]

v2 = 10:14 % 结果: [10 11 12 13 14]

语法 2: start:step:end

创建从 start 到 （小于等于）end，步长为 step 的行向量。

% 步长为 2

v3 = 1:2:10 % 结果: [1 3 5 7 9]

% 步长为负数（递减序列）

v4 = 10:-1:1 % 结果: [10 9 8 7 6 5 4 3 2 1]

% 步长为小数

v5 = 0:0.2:1 % 结果: [0 0.2 0.4 0.6 0.8 1.0]

linspace 函数

创建一个包含指定数量元素的线性等分行向量。

当关心点的数量而不是步长时，linspace 非常有用。

语法: linspace(start, end, n)

创建从 start 到 end，包含 n 个点的行向量。

注意：n 是可选的，默认值为 100。

% 创建从 0 到 2*pi，包含 100 个点的向量（常用于绘图）

x = linspace(0, 2*pi);

% 创建从 1 到 10，包含 5 个点的向量

y = linspace(1, 10, 5) % 结果: [1 3.25 5.5 7.75 10]

关键点对比

特殊矩阵

对角矩阵 (diag)

diag 函数既可以从向量创建对角矩阵，也可以从矩阵中提取对角线元素。

语法: diag(k) k=0: 主对角线 (默认)

k>0: 主对角线上方的第 k 条对角线

k<0: 主对角线下方的第 k 条对角线

% 从向量创建对角矩阵

v = [1, 2, 3];

D1 = diag(v) % 创建一个主对角线为 v 的 3×3 矩阵

% 从矩阵提取对角线

A = [1 2 3; 4 5 6; 7 8 9];

d = diag(A) % 提取 A 的主对角线，结果为 [1; 5; 9]

% 创建带偏移的对角矩阵

D2 = diag(v, 1) % 将 v 放在主对角线上方第一条对角线上

分块对角矩阵（blkdiag）

一个分块对角矩阵：

[ A  0  0  … ]

[ 0  B  0  … ]

[ 0  0  C  … ]

[ …          ]

其中，A, B, C 等是矩阵（称为“块”），而 0 代表相应大小的零矩阵。blkdiag() 函数就是专门用来构造这种特殊结构的矩阵的。

Y = blkdiag(A, B, C, …)

输入参数：A, B, C, … 可以是任意数量的矩阵、向量或标量。它们不要求具有相同的维度。

示例 ：基本用法（标量和矩阵）

% 定义输入矩阵

A = 1;          % 标量 (1×1 矩阵)

B = [2, 3; 4, 5]; % 2×2 矩阵

C = [6, 7, 8];    % 1×3 行向量

% 使用 blkdiag 创建分块对角矩阵

Y = blkdiag(A, B, C);

% 显示结果

disp('输入矩阵 A:');

disp(A);

disp('输入矩阵 B:');

disp(B);

disp('输入矩阵 C:');

disp(C);

disp('使用 blkdiag(A, B, C) 生成的矩阵 Y:');

disp(Y);

输出结果：

%输入矩阵 A:

     1

%输入矩阵 B:

     2     3

     4     5

%输入矩阵 C:

     6     7     8

%使用 blkdiag(A, B, C) 生成的矩阵 Y:

     1     0     0     0     0     0

     0     2     3     0     0     0

     0     4     5     0     0     0

     0     0     0     6     7     8

魔方矩阵 (magic)

创建一个 n x n 的矩阵，其行、列、主对角线元素之和都相等。常用于测试和演示。

M = magic(5)

希尔伯特矩阵 (hilb)

创建一个病态矩阵，常用于测试数值算法的稳定性。

H = hilb(4)

从文本文件加载矩阵

Load

最简单，适用于纯数字且格式规整的 ASCII 文件（如 .txt, .dat）。文件中的数据会以矩阵形式加载到工作区，变量名默认为文件名。

% 假设 data.txt 文件内容为:

% 1 2 3

% 4 5 6

% 7 8 9

my_matrix = load('data.txt');

Dlmread

功能更灵活，可以指定分隔符（如逗号、制表符）和要读取的范围。

% 从逗号分隔的文件中读取数据

M = dlmread('data.csv', ',');

Textscan

功能最强大，用于处理格式复杂的文本文件（如包含文本和数字混合的文件），需要配合 fopen 和 fclose 使用。

从 Excel 文件加载

Xlsread

传统函数，用于从 Excel 文件中读取数值数据。

num_data = xlsread('data.xlsx', 'Sheet1', 'B2:D10');

Readmatrix

推荐使用的新函数（R2019a 及以后），功能更强大、更一致，可以自动检测分隔符和数据类型。

M = readmatrix('data.csv');

4.4.2 矩阵元素的引用

位置索引

位置索引是通过矩阵的行列号直接引用元素的方式。

MATLAB 中使用圆括号 () 进行索引，索引值必须为正整数。(1开始)

1. 单个元素引用

通过指定行号和列号引用矩阵中的单个元素。

语法：matrix(row, column)

示例：

A = [1, 2; 3, 4];

disp(A(1, 2)); % 输出第1行第2列的元素，结果为2

2. 多个元素引用

可以通过向量的形式指定多个行或列的索引，从而引用矩阵的子矩阵。

示例：

A = [1, 2, 3; 4, 5, 6; 7, 8, 9];

disp(A(1:2, 2:3)); % 输出第1到2行、第2到3列的子矩阵

3. 冒号运算符

冒号 : 表示所有行或所有列。

示例：

A = [1, 2, 3; 4, 5, 6; 7, 8, 9];

disp(A(:, 2)); % 输出第2列的所有元素

逻辑索引

逻辑索引是通过逻辑条件筛选矩阵元素的方式，常用于条件判断和筛选。

1. 生成逻辑索引

使用逻辑表达式生成与矩阵维度相同的逻辑矩阵。

示例：

A = [1, 2, 3; 4, 5, 6; 7, 8, 9];

logicalIndex = A > 5; % 生成逻辑矩阵，标记大于5的元素

disp(A(logicalIndex)); % 输出满足条件的元素

2. 直接逻辑索引

直接在索引中使用逻辑表达式。

示例：

A = [1, 2, 3; 4, 5, 6; 7, 8, 9];

disp(A(A > 5)); % 输出大于5的元素

线性索引

线性索引是将矩阵视为一个列向量，通过单一索引值引用元素的方式。

MATLAB 按列优先顺序存储矩阵元素。

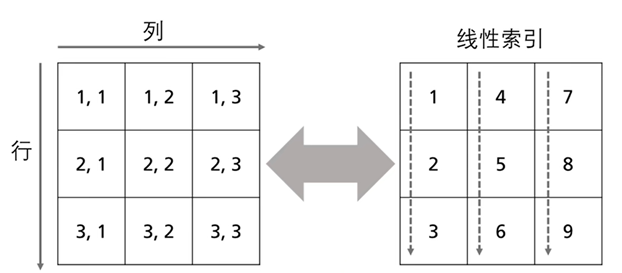
1. 单个线性索引

通过线性索引引用矩阵中的单个元素。

示例：

A = [1, 2; 3, 4];

disp(A(3)); % 输出线性索引为3的元素，结果为3

2. 线性索引与位置索引的转换

sub2ind 函数

linearIndex = sub2ind(matrixSize, rowSub, colSub)

matrixSize：矩阵的尺寸，例如 [m, n] 表示一个 m×n 的矩阵。

rowSub：行下标（可以是标量或向量）。

colSub：列下标（可以是标量或向量）。

linearIndex：返回对应的线性索引。

示例

%假设有一个 3×3 的矩阵：

A = [1, 2, 3; 4, 5, 6; 7, 8, 9];

%计算第 2 行第 3 列的线性索引：

idx = sub2ind([3, 3], 2, 3);

disp(idx); % 输出 8

ind2sub 函数

 [rowSub, colSub] = ind2sub(matrixSize, linearIndex)

matrixSize：矩阵的尺寸，例如 [m, n] 表示一个 m×n 的矩阵。

linearIndex：线性索引（可以是标量或向量）。

rowSub：返回对应的行下标。

colSub：返回对应的列下标。

示例

%假设有一个 3×3 的矩阵：

A = [1, 2, 3; 4, 5, 6; 7, 8, 9];

%计算线性索引 8 对应的行列下标：

[row, col] = ind2sub([3, 3], 8);

disp([row, col]); % 输出 [2, 3]

注意事项

行列下标必须在矩阵尺寸范围内，否则会报错。

线性索引必须在 1 到 numel(A) 之间。

注意：length()返回行和列中元素数量的最大值max(cols,rows)，numel()返回元素总数=cols*rows

在循环中尽量使用线性索引，避免频繁调用 sub2ind 或 ind2sub。

对于多维矩阵，sub2ind 和 ind2sub 的输入和输出维度必须匹配矩阵的维度。

混合索引

混合索引结合了位置索引和逻辑索引，适用于更复杂的操作。

示例：

A = [1, 2, 3; 4, 5, 6; 7, 8, 9];

rows = [1, 3]; % 指定行

cols = A(1, 🙂 > 1; % 逻辑条件指定列

disp(A(rows, cols)); % 输出满足条件的子矩阵

总结

4.4.3 矩阵元素的修改和删除

矩阵元素的修改

修改矩阵元素的核心是“先定位，后赋值”

 1. 修改单个元素

matrix(row, col) = new_value

new_value 可以是一个标量，也可以是一个与目标位置兼容的值（对于单个元素位置，通常就是标量）。

示例：

A = [1, 2, 3; 4, 5, 6; 7, 8, 9];

disp('原始矩阵 A:');

disp(A);

% 修改第 2 行第 3 列的元素为 99

A(2, 3) = 99;

disp('修改 A(2,3) 后的矩阵:');

disp(A);

输出：

%原始矩阵 A:

   1   2   3

   4   5   6

   7   8   9

%修改 A(2,3) 后的矩阵:

   1   2   3

   4   5  99

   7   8   9

2. 修改多个元素（批量修改）

matrix(rows, cols) = new_values

关键点：赋值右侧的矩阵尺寸必须与左侧选中的子矩阵尺寸完全一致！

示例：

A = magic(3); % 创建一个 3×3 的魔方矩阵

disp('原始魔方矩阵 A:');

disp(A);

% 修改第 1 行和第 3 行的所有元素

% 左侧选中了一个 2×3 的子矩阵

% 右侧也必须是一个 2×3 的矩阵

A([1, 3], 🙂 = [10, 20, 30; 70, 80, 90];

disp('修改第 1 和 3 行后的矩阵:');

disp(A);

% 修改第 2 列的所有元素为一个标量值 0

% MATLAB 会自动扩展（标量扩展）这个标量，以匹配选中的区域

A(:, 2) = 0;

disp('修改第 2 列为 0 后的矩阵:');

disp(A);

输出：

%原始魔方矩阵 A:

   8   1   6

   3   5   7

   4   9   2

%修改第 1 和 3 行后的矩阵:

  10  20  30

   3   5   7

  70  80  90

%修改第 2 列为 0 后的矩阵:

  10   0  30

   3   0   7

  70   0  90

matrix(linear_indices) = new_values

关键点： 右侧值的数量必须与 linear_indices 的数量相同。同样支持标量扩展。

示例：

A = [1, 2, 3; 4, 5, 6; 7, 8, 9];

disp('原始矩阵 A:');

disp(A);

% 修改第 1、4、7 个元素（即第一列的所有元素）

A([1, 4, 7]) = [100, 400, 700];

disp('使用线性索引修改第一列后:');

disp(A);

% 将所有大于 5 的元素乘以 10

% 这是逻辑索引和线性索引的巧妙结合

A(A > 5) = A(A > 5) * 10;

disp('将所有大于 5 的元素乘以 10 后:');

disp(A);

输出：

%原始矩阵 A:

   1   2   3

   4   5   6

   7   8   9

%使用线性索引修改第一列后:

 100   2   3

 400   5   6

 700   8   9

%将所有大于 5 的元素乘以 10 后:

 100   2   3

 400   5  60

 700  80  90

matrix(logical_matrix) = new_values

logical_matrix 必须是一个与原矩阵尺寸相同的逻辑矩阵（只包含 true 和 false）。

赋值时，只有 logical_matrix 中为 true 的位置会被修改。

右侧值的数量必须等于 logical_matrix 中 true 的数量。

同样支持标量扩展。

示例：

A = randi(10, 3, 4); % 创建一个 3×4 的随机整数矩阵

disp('原始随机矩阵 A:');

disp(A);

% 将所有偶数（能被 2 整除的数）替换为 -1

% mod(A, 2) == 0 会生成一个逻辑矩阵

A(mod(A, 2) == 0) = -1;

disp('将所有偶数替换为 -1 后:');

disp(A);

% 将矩阵中所有 NaN 值替换为 0

B = [1, 2, NaN; 4, NaN, 6; NaN, 8, 9];

disp('包含 NaN 的矩阵 B:');

disp(B);

B(isnan(B)) = 0; % isnan() 函数直接返回逻辑矩阵

disp('将 NaN 替换为 0 后的矩阵 B:');

disp(B);

输出：

%原始随机矩阵 A:

    9    2    6    5

   10   10    3    1

    2    6   10    8

%将所有偶数替换为 -1 后:

    9   -1   -1    5

   -1   -1    3    1

   -1   -1   -1   -1

%包含 NaN 的矩阵 B:

    1    2  NaN

    4  NaN    6

  NaN    8    9

%将 NaN 替换为 0 后的矩阵 B:

    1    2    0

    4    0    6

    0    8    9

矩阵元素的删除

在 MATLAB 中，不能直接删除矩阵中的“孤岛”式元素（例如，只删除 A(2,2)），因为这会破坏矩阵的矩形结构。

注意：删除操作只能针对整行或整列进行。

1. 删除行

matrix(rows_to_delete, 🙂 = []

将要删除的行的所有列赋值为空矩阵 []。

示例：

A = [1, 2, 3; 4, 5, 6; 7, 8, 9];

disp('原始矩阵 A:');

disp(A);

% 删除第 2 行

A(2, 🙂 = [];

disp('删除第 2 行后的矩阵:');

disp(A);

输出：

%原始矩阵 A:

   1   2   3

   4   5   6

   7   8   9

%删除第 2 行后的矩阵:

   1   2   3

   7   8   9

2. 删除列

matrix(:, cols_to_delete) = []

将要删除的列的所有行赋值为空矩阵 []。

示例：

A = [1, 2, 3; 4, 5, 6; 7, 8, 9];

disp('原始矩阵 A:');

disp(A);

% 删除第 1 列和第 3 列

A(:, [1, 3]) = [];

disp('删除第 1 和 3 列后的矩阵:');

disp(A);

输出：

%原始矩阵 A:

   1   2   3

   4   5   6

   7   8   9

%删除第 1 和 3 列后的矩阵:

   2

   5

   8

3. 删除满足特定条件的行（高级技巧）

创建一个逻辑向量，标记哪些行需要删除。

使用 ~ (NOT) 运算符反转逻辑向量，得到需要保留的行。

用这个逻辑向量进行索引，提取出需要保留的行，形成新矩阵。

示例：删除所有包含 NaN 的行

Data = [1, 2, 3; 4, NaN, 6; 7, 8, 9; NaN, 5, 2];

disp('原始数据 Data:');

disp(Data);

% 第一步：找出哪些行包含至少一个 NaN

% any(X, 2) 对 X 的每一行进行操作，如果该行有任何非零元素，则返回 true

% isnan(Data) 返回一个与 Data 同尺寸的逻辑矩阵

rows_with_nan = any(isnan(Data), 2);

disp('包含 NaN 的行的逻辑标记:');

disp(rows_with_nan);

% 第二步：反转逻辑，得到需要保留的行

rows_to_keep = ~rows_with_nan;

disp('需要保留的行的逻辑标记:');

disp(rows_to_keep);

% 第三步：用逻辑索引提取保留的行

CleanedData = Data(rows_to_keep, :);

disp('删除包含 NaN 的行后的 CleanedData:');

disp(CleanedData);

输出：

%原始数据 Data:

    1    2    3

    4  NaN    6

    7    8    9

  NaN    5    2

%包含 NaN 的行的逻辑标记:

  0

  1

  0

  1

%需要保留的行的逻辑标记:

  1

  0

  1

  0

%删除包含 NaN 的行后的 CleanedData:

    1    2    3

    7    8    9

注意事项

避免使用 for 循环逐个修改元素。尽量使用冒号运算符、向量和逻辑索引进行批量操作，代码更简洁，运行效率也更高。

对于基于条件的修改和筛选，逻辑索引是最直观、最强大的工具。例如 A(A > threshold) = new_value;。

在进行批量赋值时，最常犯的错误就是左右两侧的尺寸不匹配。在写代码时，心里要清楚左侧选中了多大的区域。

删除行/列 A(…) = [] 并不是在原矩阵上“挖个洞”，而是生成了一个更小的新矩阵并赋给了变量 A。对于大型矩阵，频繁的删除操作可能会因内存重新分配而影响性能。

any(isnan(A), 2) 或 any(isinf(A), 2) 结合逻辑索引，是处理含有异常值（如 NaN, Inf）的数据集的标准流程。

总结

4.4.4 矩阵的拼接和重复

矩阵的拼接

1. 水平拼接

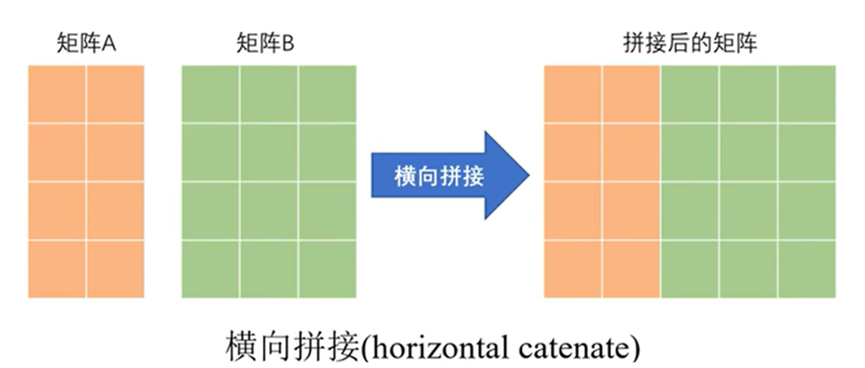
水平拼接是将矩阵并排连接，新矩阵的行数不变，列数增加。

语法：C = [A, B] 或 C = horzcat(A, B, …)

核心要求：所有参与拼接的矩阵，其行数必须相等。

示例：

A = [1, 2; 3, 4];

B = [5, 6; 7, 8];

% 使用方括号和逗号

C1 = [A, B];

% C1 =

%      1     2     5     6

%      3     4     7     8

% 使用 horzcat 函数

C2 = horzcat(A, B); % 结果与 C1 相同

注意：如果行数不匹配，MATLAB 会报错。

D = [9, 10, 11]; % 1×3 矩阵

% E = [A, D];  % 错误！使用 horzcat 的维度不一致。

% 错误信息：Error using horzcat

% Dimensions of arrays being concatenated are not consistent.

2. 垂直拼接

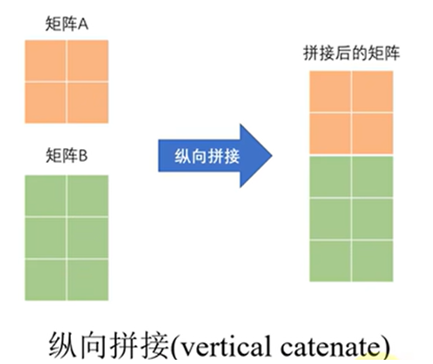
垂直拼接是将矩阵叠放连接，新矩阵的列数不变，行数增加。

语法：C = [A; B] 或 C = vertcat(A, B, …)

核心要求：所有参与拼接的矩阵，其列数必须相等。

示例：

A = [1, 2; 3, 4];

B = [5, 6; 7, 8];

% 使用方括号和分号

C1 = [A; B];

% C1 =

%      1     2

%      3     4

%      5     6

%      7     8

% 使用 vertcat 函数

C2 = vertcat(A, B); % 结果与 C1 相同

注意：如果列数不匹配，MATLAB 会报错。

F = [9; 10; 11]; % 3×1 矩阵

% G = [A; F];  % 错误！使用 vertcat 的维度不一致。

3. 多维矩阵的拼接

对于三维或更高维的矩阵，拼接操作变得更加复杂，因为需要指定沿着哪个维度进行拼接。这时，cat 函数就派上用场了。

语法：C = cat(dim, A, B, …)

参数说明：

dim：指定拼接的维度。

dim = 1：垂直拼接（沿第1维，即行方向），等同于 vertcat。

dim = 2：水平拼接（沿第2维，即列方向），等同于 horzcat。

dim = 3：沿“页”方向拼接（创建第三维）。

dim > 3：沿更高维度拼接。

注意：所有参与拼接的矩阵，在除了 dim 指定的维度之外的所有其他维度上，尺寸必须相等。

示例：

% 创建两个 2×2 的矩阵，可以看作是两个“页”

A = [1, 2; 3, 4];

B = [5, 6; 7, 8];

% 沿第3维（页）拼接

C_3d = cat(3, A, B);

% size(C_3d) 将是 [2 2 2]

% C_3d(:, :, 1) 就是 A

% C_3d(:, :, 2) 就是 B

% 沿第1维（行）拼接，等同于 vertcat

C_vert = cat(1, A, B);

% 沿第2维（列）拼接，等同于 horzcat

C_horz = cat(2, A, B);

矩阵的重复

矩阵重复是指将一个矩阵作为“砖块”，通过在行和列方向上重复它多次，来构建一个更大的、具有周期性模式的矩阵。

1. repmat 函数

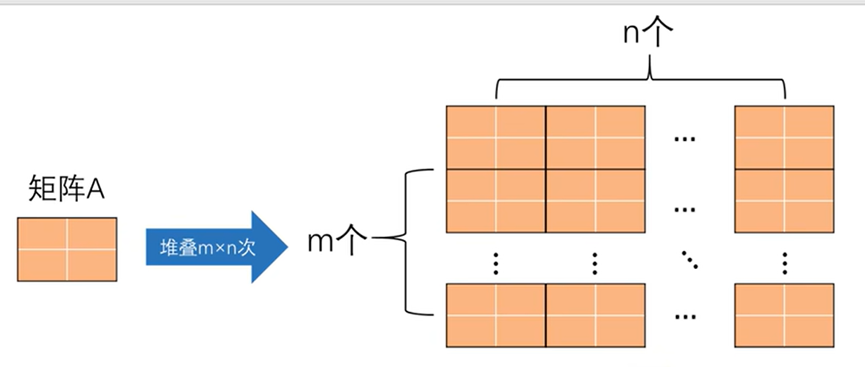
repmat（Replicate Matrix）是 MATLAB 中最常用、最强大的矩阵重复函数。

语法：B = repmat(A, m, n) 或 B = repmat(A, [m n … p])

参数说明：

A：要被重复的源矩阵（或标量、向量）。

m：在行方向上重复的次数。

n：在列方向上重复的次数。

[m n … p]：一个向量，指定在每个维度上重复的次数。这使其能够处理多维矩阵。

示例：

A = [1, 2; 3, 4];

% 将 A 在行方向重复 2 次，列方向重复 3 次

B = repmat(A, 2, 3);

% B =

%      1     2     1     2     1     2

%      3     4     3     4     3     4

%      1     2     1     2     1     2

%      3     4     3     4     3     4

% 重复一个向量

v = [10, 20];

C = repmat(v, 3, 1); % 将行向量 v 垂直堆叠 3 次

% C =

%     10    20

%     10    20

%     10    20

% 重复一个标量 (创建全值矩阵)

D = repmat(5, 2, 4); % 创建一个 2×4 的全 5 矩阵

% D =

%      5     5     5     5

%      5     5     5     5

% 这与 ones(2,4)*5 或 zeros(2,4)+5 效果相同，但 repmat 更通用。

% 多维重复

E = repmat(A, [1, 1, 2]); % 沿第3维重复2次，与 cat(3, A, A) 结果相同

2. kron 函数

kron 函数用于计算两个矩阵的克罗内克积。虽然它的数学定义更复杂，但在某些特定重复模式中，它可以作为一种高效的重复工具。

语法：K = kron(A, B)

工作原理：结果矩阵 K 是通过用矩阵 B 乘以矩阵 A 中的每一个元素，然后将这些结果块拼接起来构成的。

在重复中的应用：当 B 是一个全1矩阵时，kron 的效果就等同于 repmat。

示例：

A = [1, 2; 3, 4];

% 使用 kron 实现与 repmat(A, 2, 3) 相同的效果

% 我们需要创建一个 2×3 的全1矩阵作为 B

B_pattern = ones(2, 3);

K = kron(A, B_pattern);

% K =

%      1     1     1     2     2     2

%      1     1     1     2     2     2

%      3     3     3     4     4     4

%      3     3     3     4     4     4

% 这个结果和上面的 repmat(A, 2, 3) 完全一样。

repmat VS kron：

repmat：直观，专门用于重复整个矩阵块。repmat(A, m, n) 就是把 A 这个块重复 m 行 n 列。

kron：功能更强大，也更抽象。它不仅可以重复，还能在重复时对每个块进行缩放（由 A 的元素值决定）。对于简单的块重复，repmat 更易读、更直接。当需要 A 的元素去调制 B 的重复块时，kron 是不二之选。

3. 利用索引进行重复（高级技巧）

通过巧妙地使用索引，也可以实现重复的效果，这在某些情况下比 repmat 更快。

原理：MATLAB 支持外积式的索引。例如，A(:, v) 其中 v 是一个索引向量，会重复 A 的列。

示例：

A = [1; 2; 3]; % 一个 3×1 的列向量

% 目标：重复 A 4 次，形成一个 3×4 的矩阵

% 方法1：使用 repmat

B_repmat = repmat(A, 1, 4);

% 方法2：使用索引

% 创建一个列索引向量 [1, 1, 1, 1]

col_idx = ones(1, 4);

B_idx = A(:, col_idx); % 取 A 的第1列，重复4次

% B_idx 的结果与 B_repmat 相同。

% 对于行向量的重复

C = [10, 20, 30]; % 一个 1×3 的行向量

row_idx = ones(3, 1); % 创建一个行索引向量 [1; 1; 1]

D_idx = C(row_idx, :); % 取 C 的第1行，重复3次

% D_idx =

%     10    20    30

%     10    20    30

%     10    20    30

优点：索引操作通常在底层进行了高度优化，对于非常大的矩阵，这种方法可能比 repmat 略快。

缺点：可读性不如 repmat 直观，对于初学者来说可能难以理解。

总结

4.4.5 矩阵的重构和重新排列

矩阵的重构

矩阵重构是指改变矩阵的维度（行数、列数、页数等），但保持其总元素数量不变。这好比用同样数量的乐高积木，拼搭出不同的造型。

1. reshape – 核心重构函数

reshape 是进行矩阵重构最基本、最常用的函数。它会按照列优先的顺序，从原矩阵中取出元素，填充到新形状的矩阵中。

语法：B = reshape(A, m, n, p, …)

语法：B = reshape(A, [m n p …])

核心要求：A 的总元素数 (prod(size(A))) 必须等于新形状的总元素数 (m * n * p * …)。

关键特性：列优先(按照线性索引的顺序排列元素)。MATLAB 在内存中是按列存储矩阵的，所以 A(:) 会将 A 拉伸成一个长列向量，这个顺序就是 reshape 操作的依据。

示例：

% 创建一个 3×4 的矩阵

A = [1, 2, 3, 4;

     5, 6, 7, 8;

     9, 10, 11, 12];

disp('原始矩阵 A:');

disp(A);

% 1. 将 A 重构为 2×6 的矩阵

B = reshape(A, 2, 6);

disp('重构为 2×6 的矩阵 B:');

% B 的填充过程：

% 取 A 的第1列: [1; 5; 9] -> 填充 B 的第1列前两个元素 [1; 5]

% 取 A 的第2列: [2; 6; 10] -> 填充 B 的第1列后两个元素 [9; 2] (注意，9是A第1列最后一个)

% … 以此类推

% 最终结果：

% 1     9     2    10     3    11

% 5     6    12     7     4     8

disp(B);

% 2. 将 A 重构为一个向量（自动计算一个维度）

C = reshape(A, [], 1); % 等同于 C = A(:);

disp('重构为列向量 C:');

disp(C');

% 3. 将 A 重构为 3x2x2 的三维数组

D = reshape(A, [3, 2, 2]);

disp('重构为 3x2x2 的三维数组 D:');

disp('D(:,:,1) =');

disp(D(:,:,1));

disp('D(:,:,2) =');

disp(D(:,:,2));

2. permute – 维度置换

permute 是一个更强大的函数，用于重新排列数组的维度顺序。它不仅仅是改变形状，而是改变维度的身份。这对于处理高维数组（如图像、视频数据）至关重要。

语法：B = permute(A, order)

参数：order 是一个向量，指定了原矩阵维度在新矩阵中的位置。例如，对于一个三维数组 [行, 列, 页]，order = [2, 1, 3] 表示将原来的“列”维度放到新矩阵的“行”位置，原来的“行”维度放到新矩阵的“列”位置，而“页”维度保持不变。这相当于对每个“页”进行转置。

示例：

% 创建一个 2x3x4 的三维数组

rng('default'); % 为了结果可复现

A = randi(100, 2, 3, 4);

fprintf('原始数组 A 的尺寸: %s\\n', mat2str(size(A)));

% 1. 交换行和列维度（相当于对每一页进行转置）

B = permute(A, [2, 1, 3]);

fprintf('permute(A, [2, 1, 3]) 后的尺寸: %s\\n', mat2str(size(B)));

% 检查一下第一页

disp('A 的第一页:'); disp(A(:,:,1));

disp('B 的第一页 (A第一页的转置):'); disp(B(:,:,1));

% 2. 将页维度移动到最前面

C = permute(A, [3, 1, 2]);

fprintf('permute(A, [3, 1, 2]) 后的尺寸: %s\\n', mat2str(size(C)));

3. squeeze – 移除单一维度

当一个数组中存在某个维度的长度为 1 时（例如，从 3×1 矩阵中选取一行得到 1x1x3 的数组），squeeze 函数可以移除这些“长度为1”的维度，使数组更紧凑。

语法：B = squeeze(A)

注意：squeeze 不会移除二维矩阵的第一个或第二个单一维度。例如，squeeze(ones(1,3)) 仍然是 1×3，因为 MATLAB 认为行向量和列向量是基本的数据结构。

示例：

% 创建一个 1x3x1x2 的四维数组

A = zeros(1, 3, 1, 2);

fprintf('原始数组 A 的尺寸: %s\\n', mat2str(size(A)));

% 使用 squeeze 移除长度为1的维度

B = squeeze(A);

fprintf('squeeze(A) 后的尺寸: %s\\n', mat2str(size(B))); % 结果为 3×2

% 对二维矩阵的尝试

C = ones(1, 5);

fprintf('原始向量 C 的尺寸: %s\\n', mat2str(size(C)));

D = squeeze(C);

fprintf('squeeze(C) 后的尺寸: %s\\n', mat2str(size(D))); % 结果仍为 1×5

4. shiftdim – 维度循环移位

shiftdim 函数将数组的维度进行循环移位。它常用于将某个特定维度移动到第一维的位置，以便于进行某些操作（如 sum 等）。

语法：B = shiftdim(A, n)

参数：n 是一个整数。当 n > 0 时，维度向左（正向）移动 n 位，移出的维度在末尾循环回来。当 n < 0 时，在数组前面增加 abs(n) 个长度为1的维度。

示例：

A = rand(4, 3, 2);

fprintf('原始数组 A 的尺寸: %s\\n', mat2str(size(A)));

% 1. 维度向左移动1位

B = shiftdim(A, 1);

% 原始维度顺序: [1, 2, 3] -> [行, 列, 页]

% 新的维度顺序: [2, 3, 1] -> [列, 页, 行]

fprintf('shiftdim(A, 1) 后的尺寸: %s\\n', mat2str(size(B))); % 结果为 3x2x4

% 2. 维度向右移动（增加单一维度）

C = shiftdim(A, -1);

% 在前面增加一个长度为1的维度

fprintf('shiftdim(A, -1) 后的尺寸: %s\\n', mat2str(size(C))); % 结果为 1x4x3x2

矩阵的重新排列

与重构不同，重新排列会改变矩阵中元素的原始线性顺序。这相当于对乐高积木的顺序进行打乱，然后再重新拼装。

1. 转置 ' 和 .'

这是最常见的重新排列操作。

共轭转置 (')：对于实数矩阵，它就是普通的转置（行变列，列变行）。对于复数矩阵，它不仅进行转置，还会对每个元素取其共轭复数。

非共轭转置 (.')：只进行转置操作，不改变元素的值，即使它们是复数。

示例：

% 实数矩阵

A_real = [1, 2; 3, 4];

disp('实数矩阵 A_real:');

disp(A_real);

disp('A_real 的共轭转置 (A_real''):');

disp(A_real');

disp('A_real 的非共轭转置 (A_real.''):');

disp(A_real.');

% 复数矩阵

A_complex = [1+2i, 3-4i];

disp('复数矩阵 A_complex:');

disp(A_complex);

disp('A_complex 的共轭转置 (A_complex''):');

disp(A_complex'); % 元素变为 1-2i 和 3+4i

disp('A_complex 的非共轭转置 (A_complex.''):');

disp(A_complex.'); % 元素仍为 1+2i 和 3-4i

2. flip 系列函数 – 翻转

flip 系列函数用于沿特定方向翻转矩阵元素的顺序。

flip(A)：沿主对角线翻转元素，等同于 rot90(A, 2)。

这是 MATLAB R2016b 引入的，等同于旧版的 flipdim(A, 1)。

fliplr(A)：Flip Left-Right，左右翻转（沿垂直轴）。

flipud(A)：Flip Up-Down，上下翻转（沿水平轴）。

flip(A, dim)：沿 dim 指定的维度翻转。

示例：

A = [1, 2, 3;

     4, 5, 6;

     7, 8, 9];

disp('原始矩阵 A:');

disp(A);

disp('左右翻转 fliplr(A):');

disp(fliplr(A));

disp('上下翻转 flipud(A):');

disp(flipud(A));

% 对三维数组沿第3维（页）翻转

B = cat(3, A, A*10);

disp('三维数组 B 的第一页:');

disp(B(:,:,1));

disp('三维数组 B 的第二页:');

disp(B(:,:,2));

disp('沿第3维翻转后的第一页 (原第二页):');

disp(flip(B, 3)(:,:,1));

3. rot90 – 旋转

rot90 函数将矩阵逆时针旋转90度的整数倍。

语法：B = rot90(A)

语法：B = rot90(A, k)

其中 k 是整数，表示逆时针旋转 90*k 度。k 可以为负数，表示顺时针旋转。

示例：

A = [1, 2, 3;

     4, 5, 6];

disp('原始矩阵 A:');

disp(A);

disp('逆时针旋转90度 rot90(A):');

disp(rot90(A));

disp('逆时针旋转180度 rot90(A, 2) (等同于 flip(A)):');

disp(rot90(A, 2));

disp('顺时针旋转90度 rot90(A, -1):');

disp(rot90(A, -1));

4. sort 和 sortrows – 排序

排序是一种特殊的重新排列，它根据元素的值或特定行的值来重新组织矩阵。

sort(A)：对 A 的每一列进行升序排序。

sort(A, dim)：沿 dim 指定的维度进行排序。

sort(A, dim, 'descend')：进行降序排序。

[B, I] = sort(…)：返回排序后的矩阵 B 和索引矩阵 I。

I 记录了原始元素在新矩阵中的位置，非常有用。

sortrows(A)

根据矩阵 A 的第一列的值，对行进行升序排序。

sortrows(A, col)

根据 col 指定的列（可以是向量，如 [3, 1] 表示先按第3列排，再按第1列排）对行进行排序。

示例：

A = [3, 6, 5;

     1, 2, 4;

     4, 1, 3];

disp('原始矩阵 A:');

disp(A);

% 对每一列进行排序

disp('对每一列排序 sort(A):');

disp(sort(A));

% 对每一行进行排序

disp('对每一行排序 sort(A, 2):');

disp(sort(A, 2));

% 获取排序索引

[B, I] = sort(A(:, 1)); % 对第一列排序

disp('第一列排序后的值 B:');

disp(B');

disp('排序索引 I:');

disp(I'); % I=[2; 1; 3] 表示原A的第2个元素最小，第1个次之，第3个最大

% 根据第2列对行进行排序

disp('根据第2列对行排序 sortrows(A, 2):');

disp(sortrows(A, 2));

总结