一、卷积知识扩展
1. 二维卷积
单通道版本
对于单通道输入图像 III (尺寸 H×WH \\times WH×W) 和卷积核 KKK (尺寸 F×FF \\times FF×F),输出特征图 OOO 的计算公式为:
O(i,j)=∑m=0F−1∑n=0F−1I(i+m,j+n)⋅K(m,n)O(i,j) = \\sum_{m=0}^{F-1} \\sum_{n=0}^{F-1} I(i+m, j+n) \\cdot K(m, n)O(i,j)=m=0∑F−1n=0∑F−1I(i+m,j+n)⋅K(m,n)
计算过程示例:
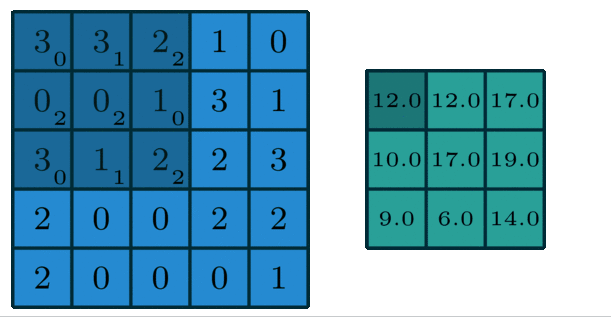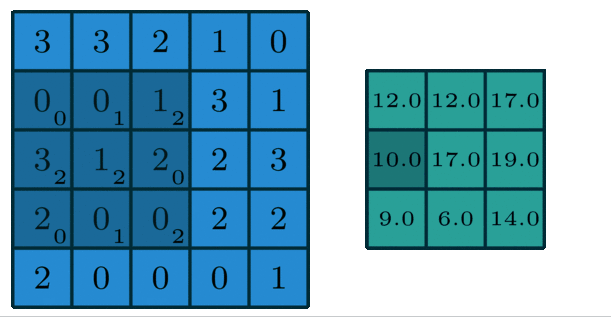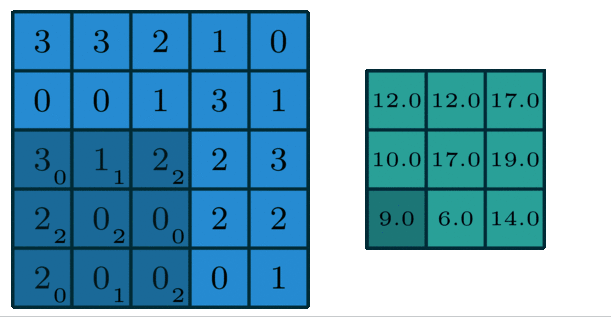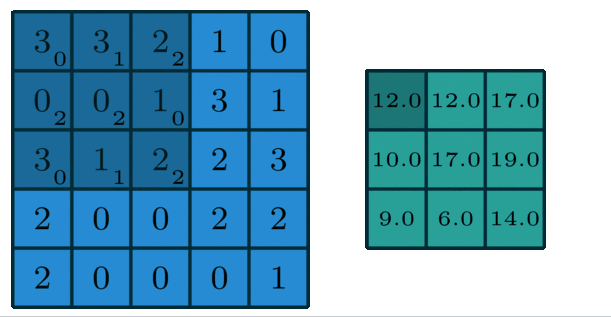
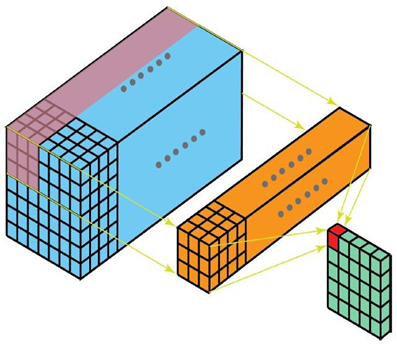
多通道版本
对于多通道输入 III (尺寸 H×W×CinH \\times W \\times C_{in}H×W×Cin) 和卷积核 KKK (尺寸 F×F×CinF \\times F \\times C_{in}F×F×Cin),输出特征图的计算公式为:
O(i,j)=∑c=0Cin−1∑m=0F−1∑n=0F−1Ic(i+m,j+n)⋅Kc(m,n)+bO(i,j) = \\sum_{c=0}^{C_{in}-1} \\sum_{m=0}^{F-1} \\sum_{n=0}^{F-1} I_c(i+m, j+n) \\cdot K_c(m, n) + bO(i,j)=c=0∑Cin−1m=0∑F−1n=0∑F−1Ic(i+m,j+n)⋅Kc(m,n)+b
其中 bbb 是偏置项,每个输出通道有独立的偏置。
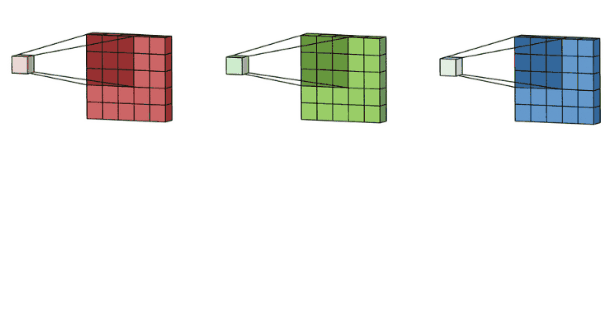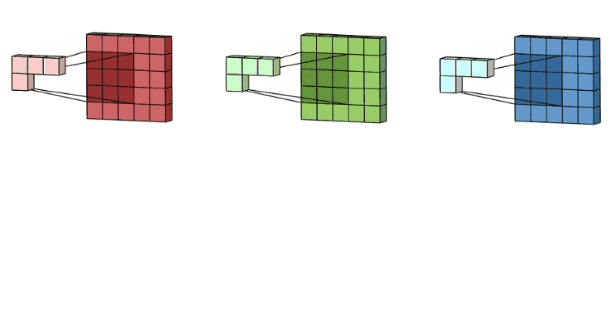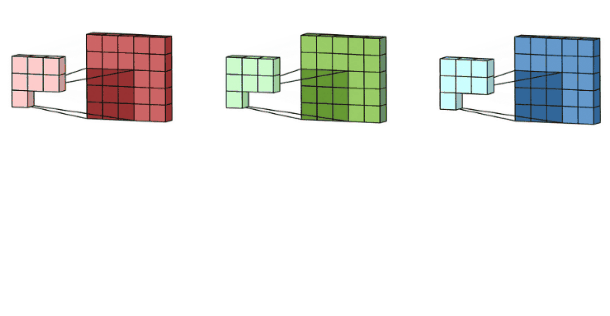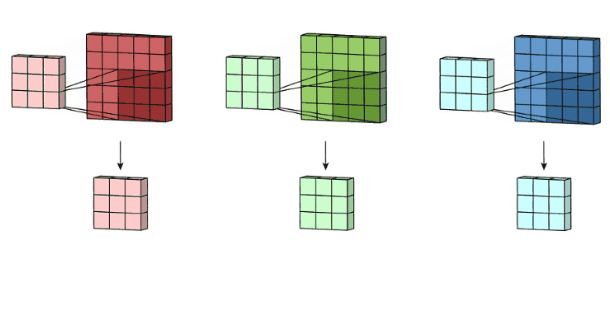

2. 三维卷积
三维卷积用于处理时空数据(如视频、3D医学影像):
- 输入维度:深度 × 高度 × 宽度 × 通道 (D×H×W×C)
- 卷积核维度:时间/深度 × 高度 × 宽度 × 输入通道 × 输出通道 (T×F×F×C_in×C_out)
- 输出计算:
O(d,i,j)=∑t=0T−1∑c=0Cin−1∑m=0F−1∑n=0F−1Ic(d+t,i+m,j+n)⋅Kc,t(m,n)O(d,i,j) = \\sum_{t=0}^{T-1} \\sum_{c=0}^{C_{in}-1} \\sum_{m=0}^{F-1} \\sum_{n=0}^{F-1} I_c(d+t, i+m, j+n) \\cdot K_{c,t}(m, n)O(d,i,j)=t=0∑T−1c=0∑Cin−1m=0∑F−1n=0∑F−1Ic(d+t,i+m,j+n)⋅Kc,t(m,n)
应用场景:
- 视频动作识别
- 3D医学图像分割
- 气象数据分析
3. 反卷积(转置卷积)
反卷积用于上采样操作,常见于图像分割和生成模型:
计算过程
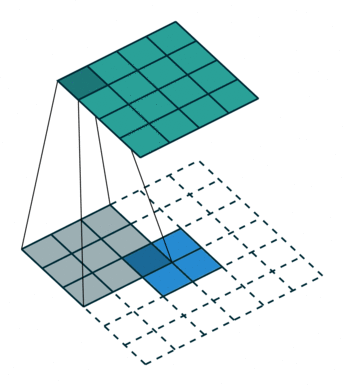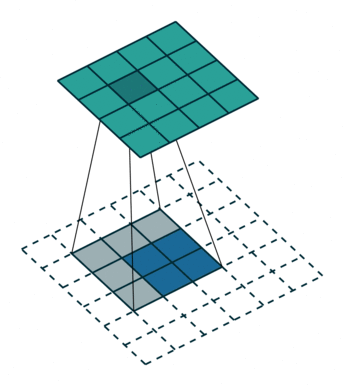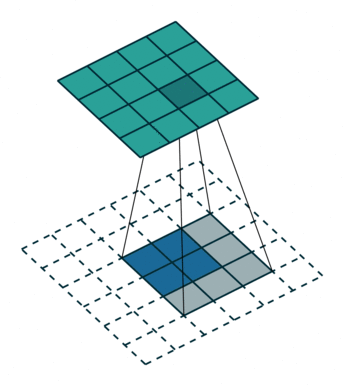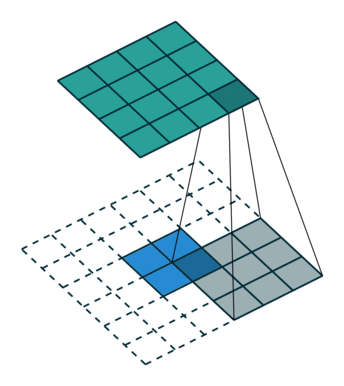
数学表示:
输入 XXX (尺寸 Hin×WinH_{in} \\times W_{in}Hin×Win),输出 YYY (尺寸 Hout×WoutH_{out} \\times W_{out}Hout×Wout):
KaTeX parse error: Expected 'EOF', got '_' at position 57: … + \\text{kernel_̲size} – 2 \\time…
底层计算:
通过矩阵转置实现:
- 标准卷积:Y=WXY = WXY=WX
- 反卷积:X=WTYX = W^TYX=WTY
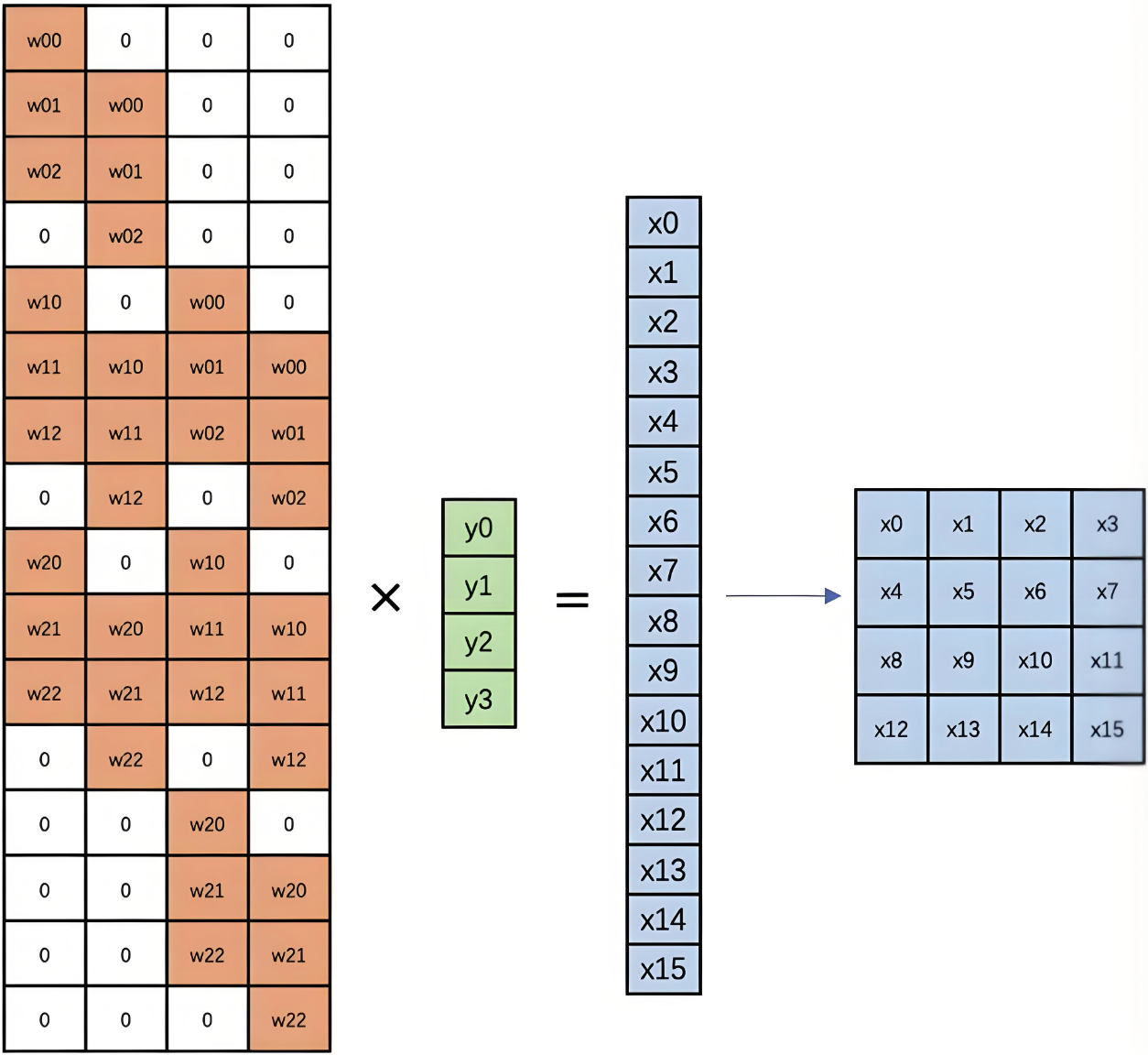
4. 膨胀卷积(空洞卷积)
膨胀卷积通过间隔采样扩大感受野:
- 膨胀率 rrr:采样间隔
- 实际感受野:F′=F+(F−1)(r−1)F' = F + (F-1)(r-1)F′=F+(F−1)(r−1)
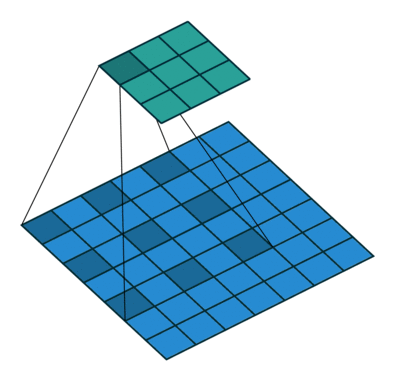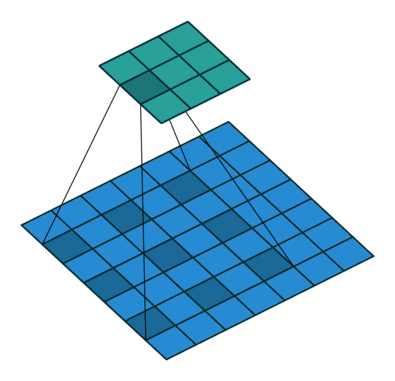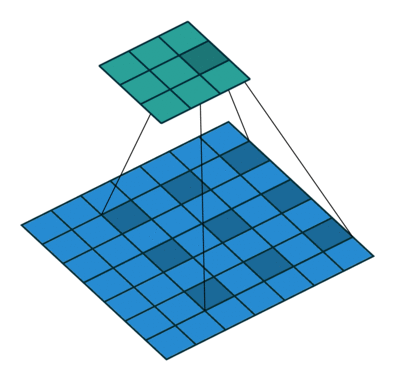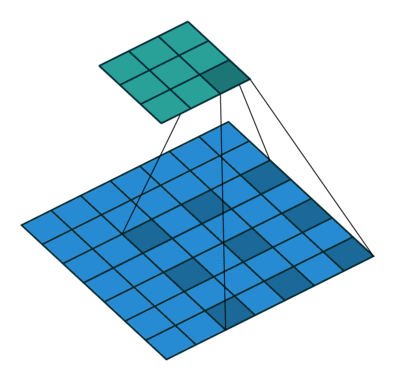
计算公式:
O(i,j)=∑m=0F−1∑n=0F−1I(i+r⋅m,j+r⋅n)⋅K(m,n)O(i,j) = \\sum_{m=0}^{F-1} \\sum_{n=0}^{F-1} I(i + r \\cdot m, j + r \\cdot n) \\cdot K(m, n)O(i,j)=m=0∑F−1n=0∑F−1I(i+r⋅m,j+r⋅n)⋅K(m,n)
优势:
- 不增加参数量的情况下扩大感受野
- 保持特征图分辨率
- 适用于语义分割(如DeepLab)
5. 可分离卷积
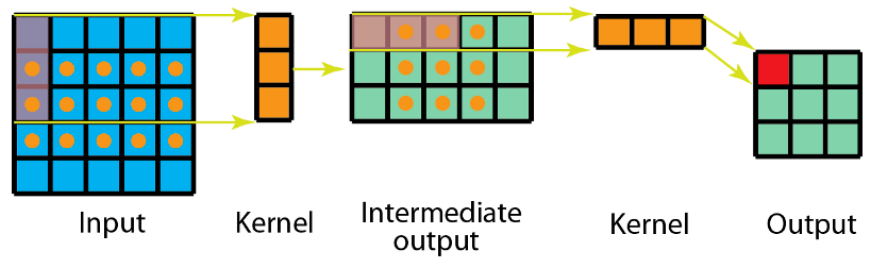
空间可分离卷积
将大卷积核分解为小核乘积:
K3x3=K3x1×K1x3K_{3×3} = K_{3×1} \\times K_{1×3}K3x3=K3x1×K1x3
原始3×3核: 分解后:
[a,b,c] [a] [x,y,z]
[d,e,f] => [d] × [x,y,z]
[g,h,i] [g]
优势:参数量从9减少到6(3+3)
图示:
深度可分离卷积
分为两步:
- 输入:H×W×CinH \\times W \\times C_{in}H×W×Cin
- 输出:H×W×CinH \\times W \\times C_{in}H×W×Cin
- 输入:H×W×CinH \\times W \\times C_{in}H×W×Cin
- 输出:H×W×CoutH \\times W \\times C_{out}H×W×Cout
参数量对比:
- 标准卷积:F×F×Cin×CoutF \\times F \\times C_{in} \\times C_{out}F×F×Cin×Cout
- 深度可分离:(F×F×Cin)+(1×1×Cin×Cout)(F \\times F \\times C_{in}) + (1 \\times 1 \\times C_{in} \\times C_{out})(F×F×Cin)+(1×1×Cin×Cout)
效率提升:MobileNet中可减少8-9倍计算量
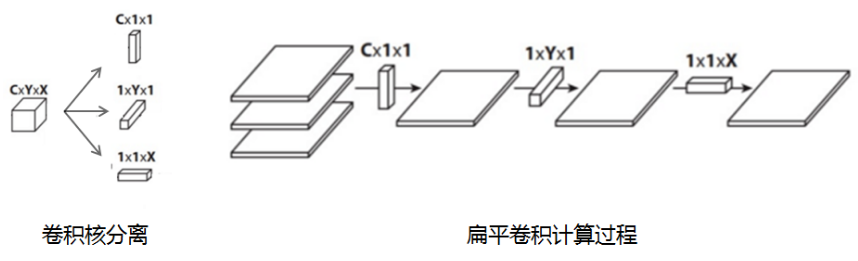
图1:输入图的每一个通道,我们都使用了对应的卷积核进行卷积。 通道数量 = 卷积核个数,每个卷积核只有一个通道

图2:完成卷积后,对输出内容进行1×1的卷积

6. 分组卷积
将输入通道分为 GGG 组,每组独立卷积:
- 标准卷积:所有输入通道→所有输出通道
- 分组卷积:组内输入通道→组内输出通道
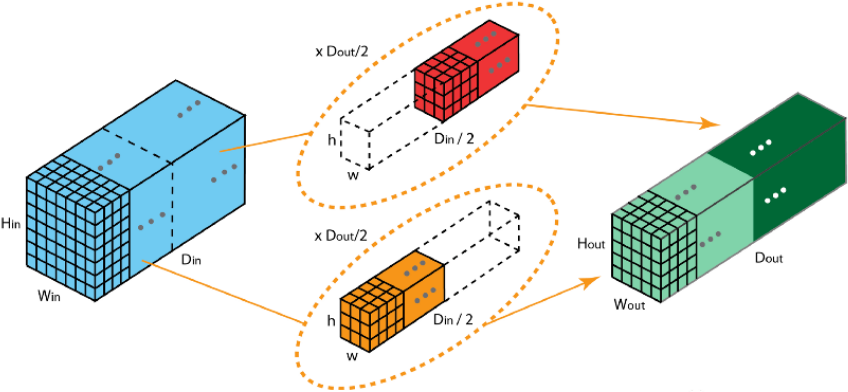
数学表达:
Og(i,j)=∑c∈groupg∑m∑nIc(i+m,j+n)⋅Kg,c(m,n)O_g(i,j) = \\sum_{c \\in \\text{group}_g} \\sum_{m} \\sum_{n} I_c(i+m,j+n) \\cdot K_{g,c}(m,n)Og(i,j)=c∈groupg∑m∑n∑Ic(i+m,j+n)⋅Kg,c(m,n)
优势:
- 减少参数量和计算量
- 促进特征多样性学习
- ResNeXt、ShuffleNet基础
7. 混洗分组卷积
在分组卷积后添加通道混洗操作:
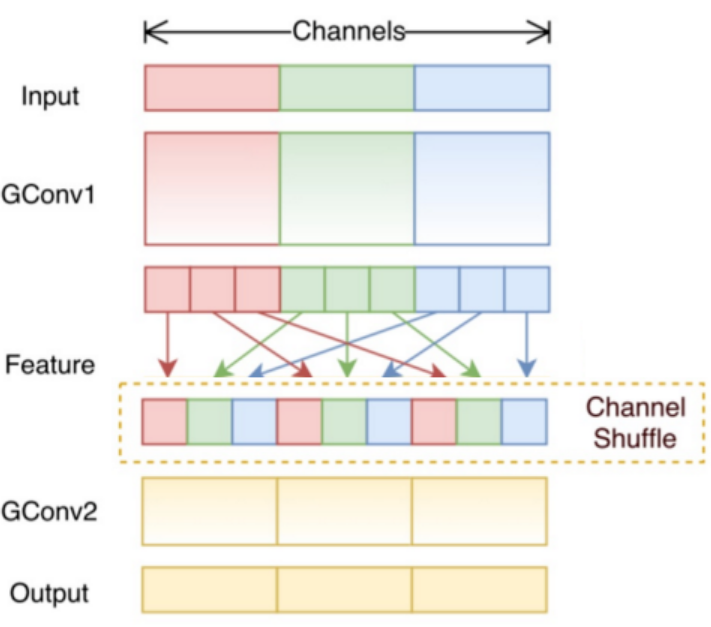
实现步骤:
#mermaid-svg-HnslONxNdCOTFjsi {font-family:\”trebuchet ms\”,verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-HnslONxNdCOTFjsi .error-icon{fill:#552222;}#mermaid-svg-HnslONxNdCOTFjsi .error-text{fill:#552222;stroke:#552222;}#mermaid-svg-HnslONxNdCOTFjsi .edge-thickness-normal{stroke-width:2px;}#mermaid-svg-HnslONxNdCOTFjsi .edge-thickness-thick{stroke-width:3.5px;}#mermaid-svg-HnslONxNdCOTFjsi .edge-pattern-solid{stroke-dasharray:0;}#mermaid-svg-HnslONxNdCOTFjsi .edge-pattern-dashed{stroke-dasharray:3;}#mermaid-svg-HnslONxNdCOTFjsi .edge-pattern-dotted{stroke-dasharray:2;}#mermaid-svg-HnslONxNdCOTFjsi .marker{fill:#333333;stroke:#333333;}#mermaid-svg-HnslONxNdCOTFjsi .marker.cross{stroke:#333333;}#mermaid-svg-HnslONxNdCOTFjsi svg{font-family:\”trebuchet ms\”,verdana,arial,sans-serif;font-size:16px;}#mermaid-svg-HnslONxNdCOTFjsi .label{font-family:\”trebuchet ms\”,verdana,arial,sans-serif;color:#333;}#mermaid-svg-HnslONxNdCOTFjsi .cluster-label text{fill:#333;}#mermaid-svg-HnslONxNdCOTFjsi .cluster-label span{color:#333;}#mermaid-svg-HnslONxNdCOTFjsi .label text,#mermaid-svg-HnslONxNdCOTFjsi span{fill:#333;color:#333;}#mermaid-svg-HnslONxNdCOTFjsi .node rect,#mermaid-svg-HnslONxNdCOTFjsi .node circle,#mermaid-svg-HnslONxNdCOTFjsi .node ellipse,#mermaid-svg-HnslONxNdCOTFjsi .node polygon,#mermaid-svg-HnslONxNdCOTFjsi .node path{fill:#ECECFF;stroke:#9370DB;stroke-width:1px;}#mermaid-svg-HnslONxNdCOTFjsi .node .label{text-align:center;}#mermaid-svg-HnslONxNdCOTFjsi .node.clickable{cursor:pointer;}#mermaid-svg-HnslONxNdCOTFjsi .arrowheadPath{fill:#333333;}#mermaid-svg-HnslONxNdCOTFjsi .edgePath .path{stroke:#333333;stroke-width:2.0px;}#mermaid-svg-HnslONxNdCOTFjsi .flowchart-link{stroke:#333333;fill:none;}#mermaid-svg-HnslONxNdCOTFjsi .edgeLabel{background-color:#e8e8e8;text-align:center;}#mermaid-svg-HnslONxNdCOTFjsi .edgeLabel rect{opacity:0.5;background-color:#e8e8e8;fill:#e8e8e8;}#mermaid-svg-HnslONxNdCOTFjsi .cluster rect{fill:#ffffde;stroke:#aaaa33;stroke-width:1px;}#mermaid-svg-HnslONxNdCOTFjsi .cluster text{fill:#333;}#mermaid-svg-HnslONxNdCOTFjsi .cluster span{color:#333;}#mermaid-svg-HnslONxNdCOTFjsi div.mermaidTooltip{position:absolute;text-align:center;max-width:200px;padding:2px;font-family:\”trebuchet ms\”,verdana,arial,sans-serif;font-size:12px;background:hsl(80, 100%, 96.2745098039%);border:1px solid #aaaa33;border-radius:2px;pointer-events:none;z-index:100;}#mermaid-svg-HnslONxNdCOTFjsi :root{–mermaid-font-family:\”trebuchet ms\”,verdana,arial,sans-serif;}输入分组卷积通道混洗输出
作用:增强组间信息交流,提升特征融合能力
8. 扁平卷积
使用1×1卷积核进行通道变换:
- 数学运算:O(i,j,c)=∑k=0Cin−1I(i,j,k)⋅W(c,k)O(i,j,c) = \\sum_{k=0}^{C_{in}-1} I(i,j,k) \\cdot W(c,k)O(i,j,c)=∑k=0Cin−1I(i,j,k)⋅W(c,k)
- 作用:
- 降维/升维
- 跨通道信息融合
- 保持空间分辨率
二、感受野
1. 感受野的概念
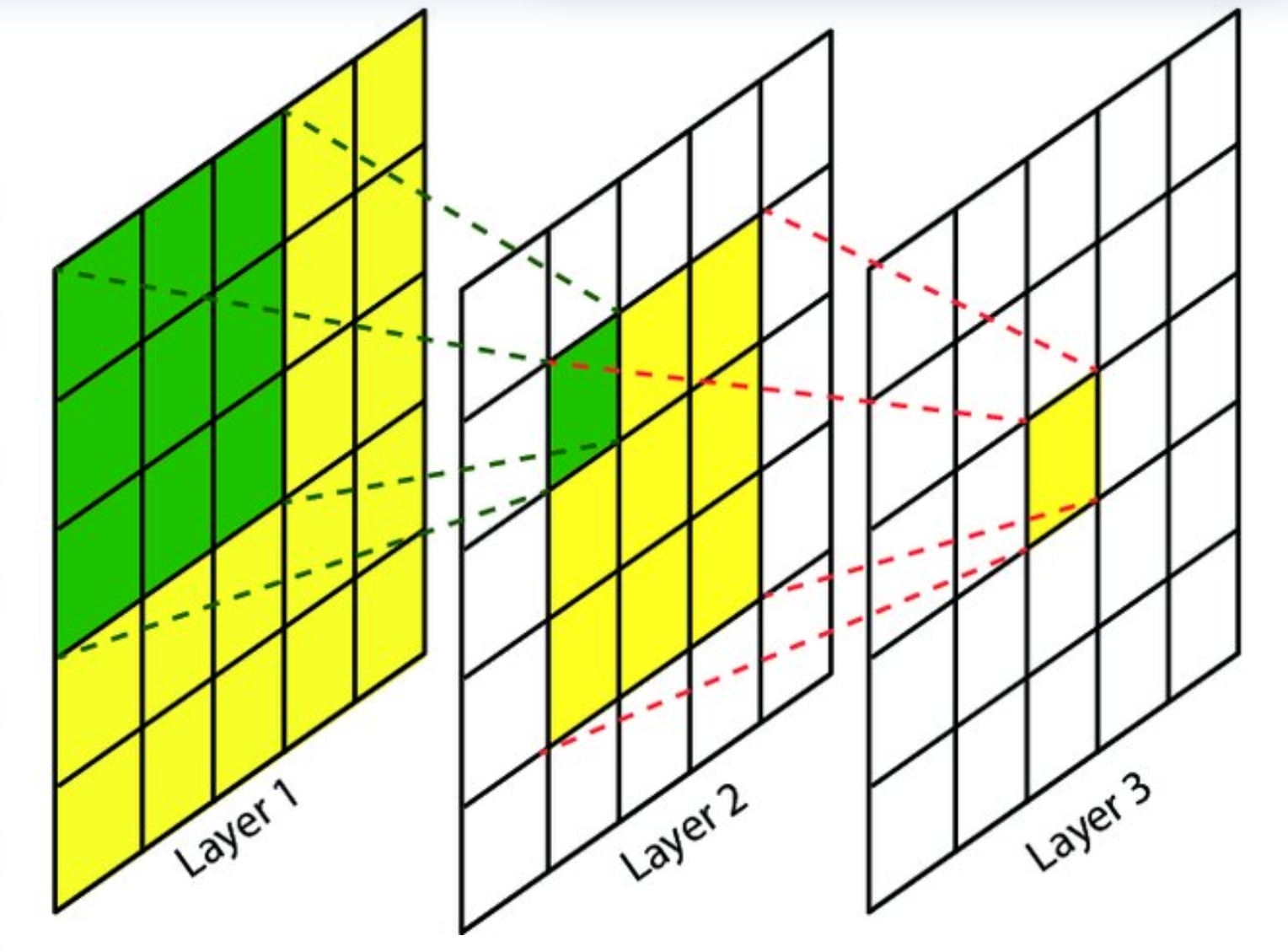
感受野指卷积网络中单个神经元对应输入图像的区域大小。它反映了神经元能"看到"的原始输入范围。
计算示例:
层1: 3×3卷积 → 感受野=3×3
层2: 3×3卷积 → 感受野=5×5 (考虑重叠)
层3: 3×3卷积 → 感受野=7×7
2. 感受野的作用
特征抽象层次
| 浅层 | 小 (3-7像素) | 边缘、纹理 |
| 中层 | 中 (15-40像素) | 形状、部件 |
| 深层 | 大 (>100像素) | 物体、场景 |
设计注意点
计算公式:
RFl=RFl−1+(kl−1)×∏i=1l−1siRF_{l} = RF_{l-1} + (k_l – 1) \\times \\prod_{i=1}^{l-1} s_iRFl=RFl−1+(kl−1)×i=1∏l−1si
其中:
- RFlRF_lRFl:第 lll 层的感受野
- klk_lkl:第 lll 层卷积核大小
- sis_isi:第 iii 层步长
三、卷积神经网络案例:CIFAR-10分类
1. 模型结构设计
#mermaid-svg-TDInMSBjGe4uHLDf {font-family:\”trebuchet ms\”,verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-TDInMSBjGe4uHLDf .error-icon{fill:#552222;}#mermaid-svg-TDInMSBjGe4uHLDf .error-text{fill:#552222;stroke:#552222;}#mermaid-svg-TDInMSBjGe4uHLDf .edge-thickness-normal{stroke-width:2px;}#mermaid-svg-TDInMSBjGe4uHLDf .edge-thickness-thick{stroke-width:3.5px;}#mermaid-svg-TDInMSBjGe4uHLDf .edge-pattern-solid{stroke-dasharray:0;}#mermaid-svg-TDInMSBjGe4uHLDf .edge-pattern-dashed{stroke-dasharray:3;}#mermaid-svg-TDInMSBjGe4uHLDf .edge-pattern-dotted{stroke-dasharray:2;}#mermaid-svg-TDInMSBjGe4uHLDf .marker{fill:#333333;stroke:#333333;}#mermaid-svg-TDInMSBjGe4uHLDf .marker.cross{stroke:#333333;}#mermaid-svg-TDInMSBjGe4uHLDf svg{font-family:\”trebuchet ms\”,verdana,arial,sans-serif;font-size:16px;}#mermaid-svg-TDInMSBjGe4uHLDf .label{font-family:\”trebuchet ms\”,verdana,arial,sans-serif;color:#333;}#mermaid-svg-TDInMSBjGe4uHLDf .cluster-label text{fill:#333;}#mermaid-svg-TDInMSBjGe4uHLDf .cluster-label span{color:#333;}#mermaid-svg-TDInMSBjGe4uHLDf .label text,#mermaid-svg-TDInMSBjGe4uHLDf span{fill:#333;color:#333;}#mermaid-svg-TDInMSBjGe4uHLDf .node rect,#mermaid-svg-TDInMSBjGe4uHLDf .node circle,#mermaid-svg-TDInMSBjGe4uHLDf .node ellipse,#mermaid-svg-TDInMSBjGe4uHLDf .node polygon,#mermaid-svg-TDInMSBjGe4uHLDf .node path{fill:#ECECFF;stroke:#9370DB;stroke-width:1px;}#mermaid-svg-TDInMSBjGe4uHLDf .node .label{text-align:center;}#mermaid-svg-TDInMSBjGe4uHLDf .node.clickable{cursor:pointer;}#mermaid-svg-TDInMSBjGe4uHLDf .arrowheadPath{fill:#333333;}#mermaid-svg-TDInMSBjGe4uHLDf .edgePath .path{stroke:#333333;stroke-width:2.0px;}#mermaid-svg-TDInMSBjGe4uHLDf .flowchart-link{stroke:#333333;fill:none;}#mermaid-svg-TDInMSBjGe4uHLDf .edgeLabel{background-color:#e8e8e8;text-align:center;}#mermaid-svg-TDInMSBjGe4uHLDf .edgeLabel rect{opacity:0.5;background-color:#e8e8e8;fill:#e8e8e8;}#mermaid-svg-TDInMSBjGe4uHLDf .cluster rect{fill:#ffffde;stroke:#aaaa33;stroke-width:1px;}#mermaid-svg-TDInMSBjGe4uHLDf .cluster text{fill:#333;}#mermaid-svg-TDInMSBjGe4uHLDf .cluster span{color:#333;}#mermaid-svg-TDInMSBjGe4uHLDf div.mermaidTooltip{position:absolute;text-align:center;max-width:200px;padding:2px;font-family:\”trebuchet ms\”,verdana,arial,sans-serif;font-size:12px;background:hsl(80, 100%, 96.2745098039%);border:1px solid #aaaa33;border-radius:2px;pointer-events:none;z-index:100;}#mermaid-svg-TDInMSBjGe4uHLDf :root{–mermaid-font-family:\”trebuchet ms\”,verdana,arial,sans-serif;}输入 32x32x3卷积64, 3x3ReLU最大池化 2×2卷积128, 3x3ReLU最大池化 2×2卷积256, 3x3ReLU全局平均池化全连接10Softmax
2. 网络模型定义
import torch.nn as nn
class CNN(nn.Module):
def __init__(self):
super(CNN, self).__init__()
self.conv1 = nn.Conv2d(3, 64, 3, padding=1)
self.pool = nn.MaxPool2d(2, 2)
self.conv2 = nn.Conv2d(64, 128, 3, padding=1)
self.conv3 = nn.Conv2d(128, 256, 3, padding=1)
self.gap = nn.AdaptiveAvgPool2d(1) # 全局平均池化
self.fc = nn.Linear(256, 10)
def forward(self, x):
x = self.pool(F.relu(self.conv1(x)))
x = self.pool(F.relu(self.conv2(x)))
x = F.relu(self.conv3(x))
x = self.gap(x)
x = x.view(–1, 256)
x = self.fc(x)
return x
3. 核心模块解析
| 卷积层 | 特征提取 | y=W∗x+by = W \\ast x + by=W∗x+b |
| ReLU | 引入非线性 | f(x)=max(0,x)f(x) = \\max(0,x)f(x)=max(0,x) |
| 最大池化 | 降维 | y=max(xi:i+k,j:j+k)y = \\max(x_{i:i+k,j:j+k})y=max(xi:i+k,j:j+k) |
| 全局平均池化 | 空间信息聚合 | yc=1H×W∑i∑jxc,i,jy_c = \\frac{1}{H \\times W} \\sum_i \\sum_j x_{c,i,j}yc=H×W1∑i∑jxc,i,j |
| Softmax | 分类概率输出 | pc=ezc∑kezkp_c = \\frac{e^{z_c}}{\\sum_{k} e^{z_k}}pc=∑kezkezc |
4. CIFAR-10数据集
-
10类物体(飞机、汽车、鸟等)
-
50,000训练图像 + 10,000测试图像
-
分辨率32×32 RGB
-
数据加载:
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))
])trainset = torchvision.datasets.CIFAR10(
root='./data', train=True, download=True, transform=transform)
5. 数据增强策略
train_transform = transforms.Compose([
transforms.RandomHorizontalFlip(), # 随机水平翻转
transforms.RandomRotation(15), # 随机旋转(-15°~15°)
transforms.ColorJitter( # 颜色调整
brightness=0.2,
contrast=0.2,
saturation=0.2
),
transforms.RandomResizedCrop(32, scale=(0.8, 1.0)), # 随机缩放裁剪
transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))
])
6. 模型训练与保存
model = CNN().cuda()
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
for epoch in range(50):
for inputs, labels in train_loader:
inputs, labels = inputs.cuda(), labels.cuda()
# 前向传播
outputs = model(inputs)
loss = criterion(outputs, labels)
# 反向传播
optimizer.zero_grad()
loss.backward()
optimizer.step()
# 每10轮保存一次
if epoch % 10 == 0:
torch.save(model.state_dict(), f'model_epoch_{epoch}.pth')
7. 模型验证流程
model.load_state_dict(torch.load('best_model.pth'))
model.eval() # 切换到评估模式
correct = 0
total = 0
with torch.no_grad():
for images, labels in test_loader:
images, labels = images.cuda(), labels.cuda()
outputs = model(images)
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
print(f'准确率: {100 * correct / total}%')
8. 实时训练可视化
使用TensorBoard记录:
from torch.utils.tensorboard import SummaryWriter
writer = SummaryWriter()
for epoch in range(epochs):
# …训练循环…
writer.add_scalar('Loss/train', loss.item(), epoch)
writer.add_scalar('Accuracy/train', acc, epoch)
# 可视化卷积核
if epoch % 5 == 0:
for name, param in model.named_parameters():
if 'conv' in name and 'weight' in name:
writer.add_histogram(name, param, epoch)
writer.add_images(f'{name}_kernels',
param.data[:8].unsqueeze(1),
epoch)
关键概念总结
卷积类型对比
| 标准卷积 | 高 | 高 | 通用模型 |
| 深度可分离 | 极低 | 极低 | 移动端模型 |
| 膨胀卷积 | 不变 | 不变 | 语义分割 |
| 分组卷积 | 减少 | 减少 | 高效模型 |
| 反卷积 | 高 | 高 | 生成模型 |
感受野计算表
| Conv1 | 3 | 1 | 3 |
| Pool1 | 2 | 2 | 4 |
| Conv2 | 3 | 1 | 8 |
| Pool2 | 2 | 2 | 12 |
| Conv3 | 3 | 1 | 20 |
 网硕互联帮助中心
网硕互联帮助中心


评论前必须登录!
注册