卫星轨道倾角的计算公式推导过程和运载火箭入轨时所在轨道平面的轨道倾角计算实操

昨天晚上在肖家河公园遛弯的时候，有小伙伴在后台留言加微信交流轨道倾角计算的问题，让我帮忙分析一下。

今天的文章就来介绍一下轨道倾角的计算公式，并给出详细的推导过程，然后给出轨道倾角计算实操示例，即采用微信公众号“弹道制导控制业余爱好者”之前发表过的文章《四级固体运载火箭弹道设计及500t推力固体火箭发动机于弹道设计实操》里面的弹道参数，计算火箭入轨点的轨道倾角。

在介绍具体的轨道倾角计算公式之前，给小伙伴们推荐一本卫星轨道方面的经典书籍《近地航天器轨道基础》，郗晓宁老师编著，国防科技大学出版社出版。

作者是在2022年4月18日花高价从淘宝网购买的二手书，新书估计够呛能有了。当时也是刚从捣蛋转行到干运载火箭没多久，关于卫星轨道方面的知识都一脸懵。好在有华哥帮忙指导，当时就是他推荐了郗晓宁老师编著的《近地航天器轨道基础》一书，里面的知识很实用，贴近工程实际。

该书作为近地航天器轨道基础知识的教材，主要内容包括三个部分。第二章至第五章为与近地航天器轨道有关的坐标系统和时间系统；第六章至第八章为航天器轨道力学的基础知识，如二体问题及其轨道摄动；第九章至第十二章为近地航天器(如卫星、星座和月球探测器)轨道的初步设计，还论述了航天器的相对运动与轨道机动的问题。

作者刚开始从事运载火箭入轨弹道优化设计工作时，对一些待优化参数变量的初始值选取问题不太清楚，或者说没有直观的物理概念，觉得选啥初始值都是可行的，没什么约束可言。但实际情况不是这样的，以运载火箭的初始射向为例。

在酒泉卫星发射中心发射太阳同步轨道，由于太阳同步轨道的轨道倾角大于90°，属于逆轨运行，运载火箭的射向需要设定为西南方向，这跟发射场的纬度、轨道倾角都有关系。

在《近地航天器轨道基础》这本书的第116页，编者论述了发射场的位置对运载火箭射向的影响。假如S为航天器发射点，发射点的地心纬度为phiI，运载火箭射向角为AI，目标轨道的轨道倾角为i，假设地球为正圆形，不考虑地球自转，可得地心纬度phiI、运载火箭射向角AI和目标轨道倾角i的球面三角关系式为

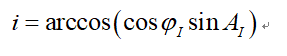
因为sinAI≤1，则phiI≤i≤180°-phiI，所以发射场离赤道越近，可以获得的轨道倾角的范围就越大。设发射点所能达到的最小轨道倾角为imin=phiI、最大的轨道倾角为imax=180°-phiI，超过这个轨道倾角范围，就需要运载火箭在飞行后期做横侧向机动了，这会带来火箭运力的损失，这也是为什么很多的航天发射场都选择建在低纬度地区，能对大部分轨道倾角的目标轨道一次性直接入轨，节省燃料提升运力。

太阳同步轨道，轨道倾角i大于90°，那么cos(phiI)*sin(AI)的值就是负数，而cos(phiI)大于0，因此sin(AI)的值就得小于0，AI的取值范围是180°~360°。举个例子，发射场纬度为41.118°，目标轨道倾角为98.18663°，通过上面的公式可以算得射向角AI=190.8955°，往西南方向。由于地球是椭球体，不是正圆形，因此在进行运载火箭弹道优化设计时，可以将190.8955°作为射向角AI的初始值，这样优化求解器的工作量会大幅降低，优化求解效率也会大大提高，后续经优化求解得到的射向角AI=192.7°，两者只差了不到2°。

《近地航天器轨道基础》的第七章介绍了二体问题，具体内容包括二体问题运动方程及其解、轨道根数与位置矢量、速度矢量的关系、两个时刻的位置矢量和速度矢量的关系、f和g级数、球坐标表示的运动状态参数。

今天的文章从二体问题运动方程开始推导轨道倾角的计算公式。

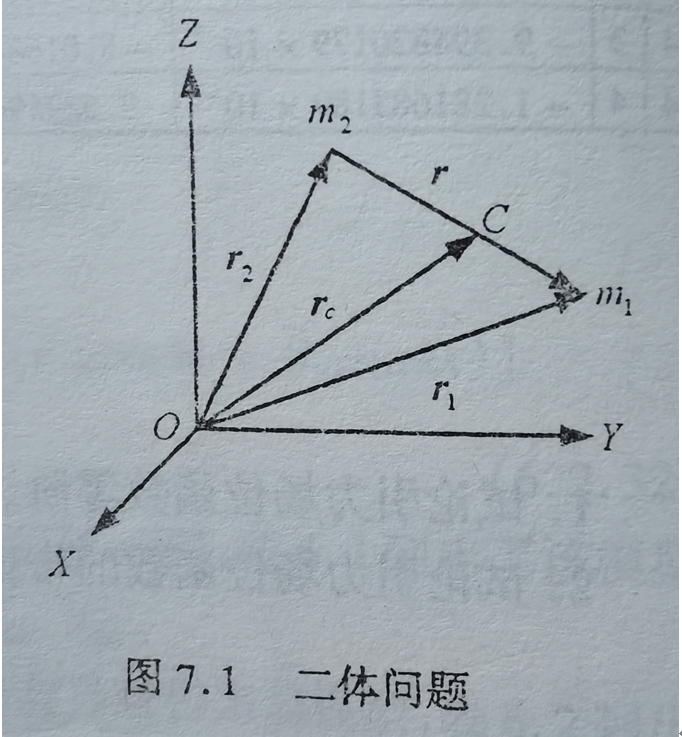
如上图所示，O-XYZ为惯性坐标系，两个天体的质量分别为m1和m2，它们的位置矢量分别为r1和r2，它们之间的相对位置矢量为r=r1-r2，设m1和m2的质量中心C点的位置矢量为rc，根据质量中心的位置计算公式可得

基于上面的式子可以得到r1与rc和r2与rc的矢量差值为

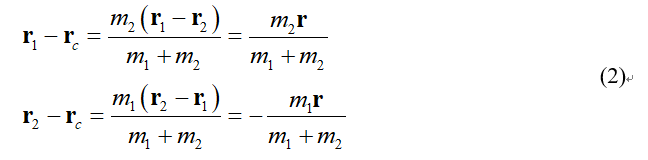
上面的式子分别表示了质量中心C到m1和m2的相对位置矢量。再设作用于m1的力为F1，作用于m2的力为F2，则有

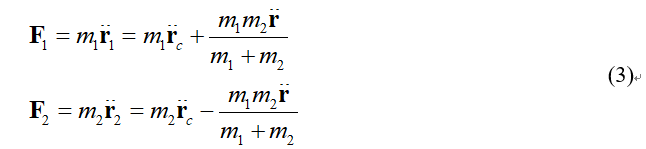
根据牛顿第三定律，两个物体间的相互作用力大小相等、方向相反、作用在同一直线上，可得

将式(3)代入式(4)可得

式(5)只有在位置矢量rc的二阶导数为0时才成立，因此二体系统的质量中心永无加速度。将位置矢量rc的二阶导数为0这一结果代入式(3)可得

根据牛顿万有引力定律可得质量m1受到的质量m2施加的引力为

整理式(6)和(7)可得

式(8)是m1相对于m2的运动方程，也是二体系统的基本运动微分方程。它是一个六阶非线性常微分方程组，若要完全求解该方程组，必须找出包含六个相互独立的积分常数的解。

面积积分。根据矢量运算法则可得

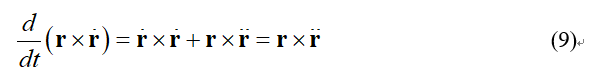
用位置矢量r叉乘式(8)可得

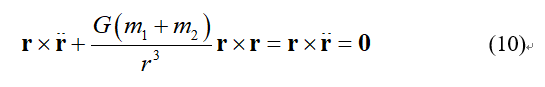
将式(10)代入式(9)可得

则

在式(12)中，矢量h为积分常矢量。设在惯性坐标系O-XYZ中，矢量h为

则hX、hY、hZ是积分常数。分析式(12)可得下面的结论。

(1)矢量h表示的是单位质量的动量矩；(2)因为矢量h是常矢量，所以二体系统的动量矩是守恒的；(3)因为矢量h垂直于矢量r和矢量r的导数，故矢量h垂直于运动平面，所以该运动平面必须是惯性固定的。如下图所示，可以用相对惯性坐标系O-XYZ的XY平面的倾角i和轨道升交点的经度omega表示轨道平面的方向。

为便于分析，以轨道平面为基准平面建立轨道坐标系，记为O-x’y’z’，其x’轴与矢量r重合，z’轴与矢量h重合，y’轴与x’轴和z’轴构成右手坐标系，如下图所示。

在轨道坐标系O-x’y’z’中，有如下的表达式

在式(14)中，h为矢量h的模值，r为径向距离(即位置矢量r的模值)，r_dot为径向速度，u_dot为周方向(即轨道平面内垂直于矢径方向)的角速度，r*u_dot为周向速度。在上图中，设u为从轨道升交点的方向到x’轴指向之间的夹角，称为纬度幅角，当-90°≤u≤90°时，称为轨道的升段，当90°≤u≤270°时，称为轨道的降段。

惯性坐标系O-XYZ与轨道坐标系O-x’y’z’的转换关系为

将积分常矢量h分别在惯性坐标系O-XYZ与轨道坐标系O-x’y’z’投影，可得

对式(16)做个转置变换，可得

由式(17)可得

由式(18)即可算出轨道倾角i和轨道升交点的经度omega。

计算实例：运载火箭入轨时刻的轨道倾角计算实操，弹道数据来源于公众号之前发的文章《》，入轨时刻地心到火箭的矢径在地心惯性坐标系的分量分别为-15628.869750923594m、7078022.3086325200m、-37027.039039880910m，火箭相对地心惯性坐标系的速度(也称为绝对速度，相比地速多了个因为地球自转而附加的牵连速度)在地心惯性坐标系的分量分别为1068.6930311928195m/s、-36.496587897375761m/s、-7427.7105230230009m/s，将位置矢量和速度矢量做叉乘，可得积分常矢量h在地心惯性坐标系下的分量分别为-52574852144.606224、-155657258.89951625、-7563662715.4442844，根据式(18)可求得运载火箭入轨时所在轨道平面的轨道倾角i为

好了，今天的交流就到这了，下期再聊。

关注微信公众号：弹道制导控制业余爱好者。