无监督学习是机器学习的重要分支,它从无标签数据中发现隐藏模式和结构。以下是关于无监督学习的深度解析:
一、核心概念
1. 定义与特点
无监督学习处理没有预先标记的数据集,目标是:
-
发现数据中的隐藏模式
-
识别内在结构
-
提取有意义特征
2. 与监督学习的对比
|
数据要求 |
无需标签 |
需要标注数据 |
|
目标 |
发现结构 |
预测输出 |
|
应用场景 |
探索性分析 |
预测性任务 |
|
典型算法 |
K-means, PCA |
回归, 分类 |
二、主要算法分类
1. 聚类分析
将相似数据分组:
-
K-means:基于距离的划分聚类
-
层次聚类:构建树状聚类结构
-
DBSCAN:基于密度的聚类
-
高斯混合模型(GMM):概率软聚类
2. 降维技术
减少特征维度:
-
PCA:主成分分析(线性)
-
t-SNE:t分布随机邻域嵌入(非线性)
-
UMAP:统一流形逼近与投影
-
自动编码器:神经网络降维
3. 关联规则学习
发现变量间关系:
-
Apriori:频繁项集挖掘
-
FP-Growth:高效频繁模式发现
4. 异常检测
识别异常点:
-
孤立森林
-
局部离群因子(LOF)
-
一类SVM
三、k-means聚类
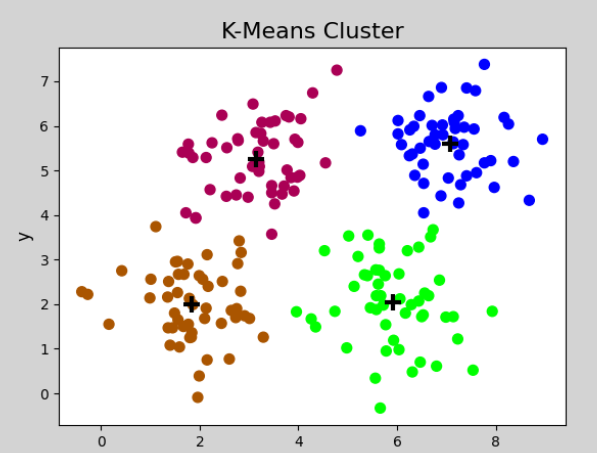
K-means是最经典且广泛使用的聚类算法之一,属于无监督学习。下面我将全面介绍K-means的原理、实现和应用。
算法原理
k-means 聚类的核心目标是将 n 个数据点划分到 k 个簇中,通过优化以下两个条件来达到最佳的聚类效果:
数据点归属原则:
- 每个数据点会被分配到距离最近的簇中心所在的簇。具体来说,对于数据集中的每一个点,计算它与所有簇中心(质心)的欧氏距离,然后将其归入距离最短的那个簇。
- 公式化表示:对于数据点 ( x_i ),其所属的簇 ( C_j ) 满足 ( j = \\text{argmin}_k ||x_i – \\mu_k||^2 ),其中 ( \\mu_k ) 是第 k 个簇的中心。
优化目标:
- 算法通过迭代优化,使得所有簇内数据点到其簇中心的平方距离和(也称为簇内平方和,Within-Cluster Sum of Squares, WCSS)最小化。
- 数学表达式:最小化目标函数
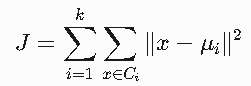
其中:
-
Ci:第i个簇
-
μi:第i个簇的质心
-
x:数据点
算法步骤的详细说明:
初始化:
- 随机选择 k 个数据点作为初始的簇中心(质心)。这一步对最终聚类结果有较大影响,常见的改进方法包括 k-means++ 初始化,以减少对初始中心的敏感性。
分配阶段:
- 遍历所有数据点,计算每个点到当前各个簇中心的距离,并将其分配到最近的簇。通常使用欧氏距离,但也可以根据具体问题选择其他距离度量(如曼哈顿距离)。
更新阶段:
- 重新计算每个簇的中心,即取簇内所有数据点的均值作为新的质心。例如,对于簇 ( C_j ),其新中心 ( \\mu_j ) 更新为 ( \\mu_j = \\frac{1}{|C_j|} \\sum_{x_i \\in C_j} x_i )。
迭代优化:
- 重复分配和更新步骤,直到满足停止条件(如质心变化小于某个阈值,或目标函数 ( J ) 的变化不再显著)。
应用场景示例:
- 客户细分:在市场营销中,根据客户的购买行为、 demographics 等特征,将客户分成不同的群体,以便制定个性化策略。
- 图像压缩:通过将图像中颜色相近的像素聚类,用少量代表性颜色替代原始颜色,减少存储空间。
- 异常检测:通过聚类分析,将正常数据和异常数据分离,例如在网络安全中识别异常流量。
注意事项:
- 需要预先指定簇的数量 k,选择不合适的 k 值可能导致聚类效果不佳。可以通过肘部法则(Elbow Method)或轮廓系数(Silhouette Score)来确定最佳 k 值。
- 对噪声和异常值敏感,因为平方距离会放大离群点的影响。改进方法包括使用 k-medoids 或其他鲁棒性更强的算法。
通过以上步骤和优化目标,k-means 能够高效地将数据划分为具有高内聚性的簇,适用于大规模数据集的聚类任务。
四、k-means聚类的使用
class sklearn.cluster.KMeans( n_clusters=8, *, init='k-means++', n_init='auto', max_iter=300, tol=1e-4, verbose=0, random_state=None, copy_x=True, algorithm='lloyd' )
二、核心参数详解
1. 聚类配置参数
|
n_clusters |
int |
要形成的簇数(k值) |
通过肘部法则确定 |
|
init |
str/array |
初始化方法 |
'k-means++'(默认) 或 'random' |
|
n_init |
int/str |
不同初始化的运行次数 |
'auto' 或 10(默认) |
|
algorithm |
str |
K-means算法变体 |
'lloyd'(默认), 'elkan' |
2. 优化控制参数
|
max_iter |
int |
单次运行的最大迭代次数 |
300(默认) |
|
tol |
float |
收敛阈值 |
1e-4(默认) |
|
random_state |
int |
随机种子 |
任意整数(保证可复现) |
三、主要属性
训练后模型将获得以下重要属性:
|
cluster_centers_ |
簇中心坐标 |
(n_clusters, n_features) |
|
labels_ |
每个样本的簇标签 |
(n_samples,) |
|
inertia_ |
样本到最近簇中心的平方距离和 |
标量 |
|
n_iter_ |
实际迭代次数 |
标量 |
四、核心方法
1. 训练模型
fit(X, y=None, sample_weight=None)
-
X:训练数据,形状 (n_samples, n_features)
-
sample_weight:样本权重,形状 (n_samples,)
2. 预测簇标签
predict(X, sample_weight=None)
返回每个样本所属的簇
3. 训练并预测
fit_predict(X, y=None, sample_weight=None)
一步完成训练和预测
4. 模型评分
score(X, y=None, sample_weight=None)
返回负的inertia值(越大越好)
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
# 生成样本数据
X, _ = make_blobs(n_samples=300, centers=4, random_state=42)
# 创建KMeans实例
kmeans = KMeans(
n_clusters=4,
init='k-means++',
n_init=10,
max_iter=300,
random_state=42
)
# 训练模型
kmeans.fit(X)
# 可视化结果
plt.scatter(X[:, 0], X[:, 1], c=kmeans.labels_, cmap='viridis')
plt.scatter(kmeans.cluster_centers_[:, 0],
kmeans.cluster_centers_[:, 1],
s=200, marker='*', c='red')
plt.title('K-means Clustering')
plt.show()
 网硕互联帮助中心
网硕互联帮助中心




评论前必须登录!
注册