结合逻辑回归的核心原理、数学推导与工程实践进行系统化阐述:
逻辑回归:从线性回归到分类决策的演化
为何名为“回归”却用于分类?揭秘Sigmoid函数的桥梁作用与决策边界本质
一、问题起源:线性回归为何不能直接用于分类?
回归 vs 分类的本质差异
- 线性回归:输出连续值(如房价预测),拟合直线最小化误差(如均方误差)
- 分类任务:输出离散类别(如红/绿点分类),需找到决策边界分离数据
- 关键矛盾:线性回归的输出范围是(−∞,+∞)(-\\infty, +\\infty)(−∞,+∞),无法直接映射到类别标签(0/1)
直接使用线性回归的缺陷
- 若强行设定阈值(如 y>0.5y>0.5y>0.5 判为正类),存在两大问题:
- 输出值无概率意义(可能超出[0,1]范围)
- 分段函数不可导,无法优化参数
例:二维空间中,线性方程 y=θ0+θ1×1+θ2x2y = \\theta_0 + \\theta_1x_1 + \\theta_2x_2y=θ0+θ1x1+θ2x2 无法将红绿点分到直线两侧
二、核心突破:Sigmoid函数如何连接回归与分类?
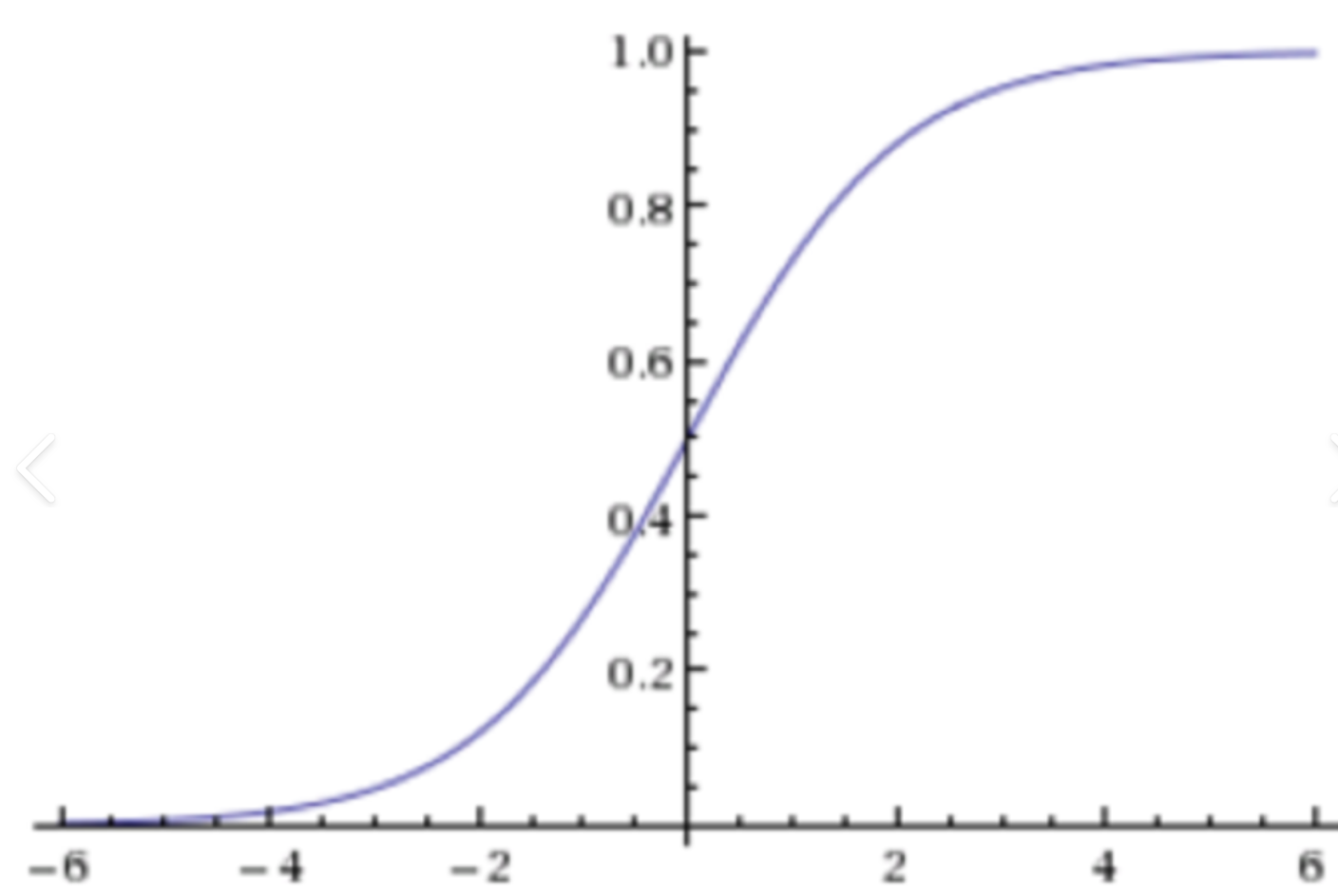
Sigmoid函数的数学魔力
σ(z)=11+e−z其中 z=θTx\\sigma(z) = \\frac{1}{1 + e^{-z}} \\quad \\text{其中 } z = \\theta^Txσ(z)=1+e−z1其中 z=θTx
- 值域压缩:将任意实数 zzz 映射到 (0,1)(0,1)(0,1) 区间,输出可解释为概率
- 可导性:导数 σ′(z)=σ(z)(1−σ(z))\\sigma'(z) = \\sigma(z)(1-\\sigma(z))σ′(z)=σ(z)(1−σ(z)),便于梯度下降优化
- 决策规则:
y^={1if σ(z)≥0.50otherwise\\hat{y} = \\begin{cases} 1 & \\text{if } \\sigma(z) \\geq 0.5 \\\\ 0 & \\text{otherwise} \\end{cases}y^={10if σ(z)≥0.5otherwise
为何不用分段函数?
- 分段函数(如 z>0z>0z>0 输出1)不可导,无法通过梯度下降求解参数 θ\\thetaθ
- Sigmoid提供平滑近似,保留可导性且逼近阶跃函数
三、数学推导:从概率建模到参数优化
概率建模
- 正类概率: P(y=1∣x)=σ(θTx)=11+e−θTxP(y=1|x) = \\sigma(\\theta^Tx) = \\frac{1}{1+e^{-\\theta^Tx}}P(y=1∣x)=σ(θTx)=1+e−θTx1
- 负类概率: P(y=0∣x)=1−P(y=1∣x)P(y=0|x) = 1 – P(y=1|x)P(y=0∣x)=1−P(y=1∣x)
损失函数:交叉熵(Cross-Entropy)
- 通过极大似然估计推导:
L(θ)=∏i=1nP(yi∣xi;θ)=∏i=1ny^iyi(1−y^i)1−yiL(\\theta) = \\prod_{i=1}^n P(y_i|x_i;\\theta) = \\prod_{i=1}^n \\hat{y}_i^{y_i} (1-\\hat{y}_i)^{1-y_i}L(θ)=∏i=1nP(yi∣xi;θ)=∏i=1ny^iyi(1−y^i)1−yi - 取负对数似然得损失函数:
J(θ)=−1n∑i=1n[yiln(y^i)+(1−yi)ln(1−y^i)]J(\\theta) = -\\frac{1}{n} \\sum_{i=1}^n \\left[ y_i \\ln(\\hat{y}_i) + (1-y_i) \\ln(1-\\hat{y}_i) \\right]J(θ)=−n1∑i=1n[yiln(y^i)+(1−yi)ln(1−y^i)]
注:此函数凸性保证梯度下降收敛到全局最优
梯度下降优化
- 梯度计算:
∇θJ=1nXT(σ(Xθ)−y)\\nabla_\\theta J = \\frac{1}{n} X^T (\\sigma(X\\theta) – y)∇θJ=n1XT(σ(Xθ)−y) - 参数更新:
θ:=θ−α∇θJ\\theta := \\theta – \\alpha \\nabla_\\theta Jθ:=θ−α∇θJ
(α\\alphaα 为学习率)
四、决策边界:线性与非线性拓展
线性决策边界
- 当 σ(z)=0.5\\sigma(z)=0.5σ(z)=0.5 时 z=0z=0z=0,即 θTx=0\\theta^Tx = 0θTx=0 为分类超平面
例:二维空间中为直线,三维为平面
非线性边界拓展
- 通过特征工程引入多项式项(如 x12,x1x2x_1^2, x_1x_2x12,x1x2)
- 核函数(Kernel Trick)映射高维空间(需配合正则化防过拟合)
五、代码实现:Python实战示例
import numpy as np
class LogisticRegression:
def __init__(self, lr=0.01, n_iters=1000):
self.lr = lr # 学习率
self.n_iters = n_iters # 迭代次数
self.weights = None # 权重参数
self.bias = None # 偏置项
def _sigmoid(self, z):
return 1 / (1 + np.exp(-z)) # Sigmoid激活函数
def fit(self, X, y):
n_samples, n_features = X.shape
self.weights = np.zeros(n_features)
self.bias = 0
# 梯度下降优化
for _ in range(self.n_iters):
z = np.dot(X, self.weights) + self.bias
y_pred = self._sigmoid(z)
# 计算梯度
dw = (1 / n_samples) * np.dot(X.T, (y_pred – y))
db = (1 / n_samples) * np.sum(y_pred – y)
# 更新参数
self.weights -= self.lr * dw
self.bias -= self.lr * db
def predict(self, X, threshold=0.5):
z = np.dot(X, self.weights) + self.bias
y_prob = self._sigmoid(z)
return (y_prob >= threshold).astype(int) # 按阈值分类
关键步骤说明:
- fit() 中梯度计算对应公式 ∇θJ\\nabla_\\theta J∇θJ
- 预测时以0.5为默认阈值
六、工业应用与局限
| 金融风控 | 用户违约概率预测 | 可解释性强(权重代表特征影响) |
| 医疗诊断 | 疾病阳性概率判断 | 计算高效,适合实时系统 |
| 推荐系统 | 用户点击/购买行为预测 | 对稀疏特征鲁棒性好 |
局限性:
- 仅适合线性可分数据(需特征工程或高阶拓展)
- 对异常值敏感(需数据清洗或正则化)
- 多分类需扩展(如OvR, Softmax)
结语:为什么逻辑回归是分类基石?
逻辑回归通过 Sigmoid函数 架起回归与分类的桥梁,其核心价值在于:
“逻辑回归的智慧在于:用连续的数学工具解决离散的决策问题,这正是机器学习的艺术。” —— 算法设计者视角
完整代码与数据集:GitHub示例链接
扩展阅读:《统计学习导论》第4章(逻辑回归与广义线性模型)
 网硕互联帮助中心
网硕互联帮助中心




评论前必须登录!
注册