基于Python的四旋翼无人机仿真系统：从欧拉积分到Streamlit交互式可视化

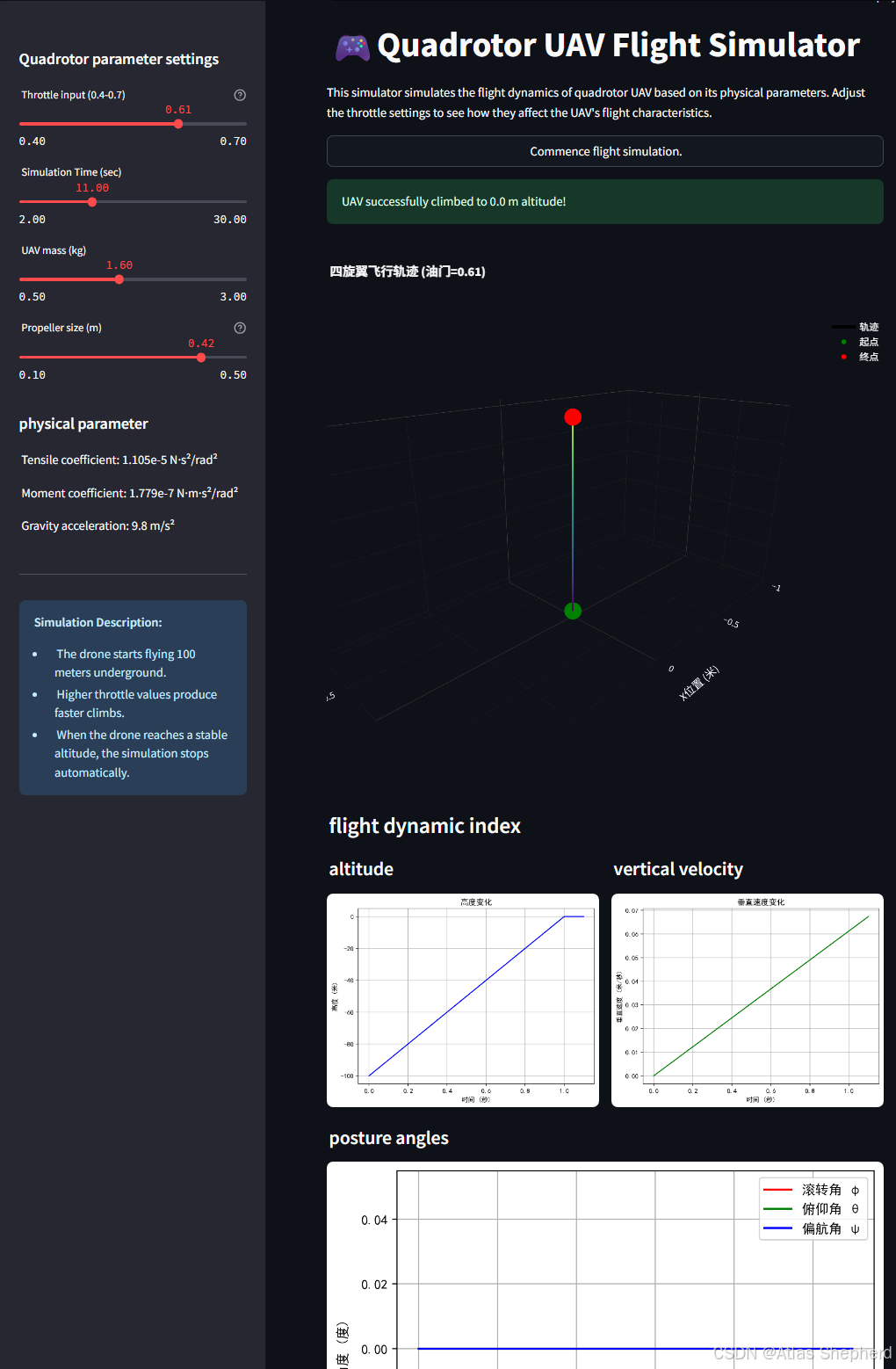
基于四旋翼无人机物理模型的仿真系统，然后通过Streamlit提供交互式可视化界面。以下是代码的结构分析、潜在问题及优化建议：

代码结构

import streamlit as st
import numpy as np
import math
import matplotlib.pyplot as plt
import plotly.graph_objects as go
import matplotlib.font_manager as fm

# 设置支持中文的字体
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号

class QuadcopterParams:
def __init__(self):
# 电机参数
self.C_r = 1148
self.w_b = -141.4
self.T_m = 0.02

# 物理参数
self.c_T = 1.105e-5 # 螺旋桨拉力系数
self.c_M = 1.779e-7 # 螺旋桨力矩系数
self.d = 0.225 # 机体中心和任一电机的距离(m)
self.m = 1.4 # 质量(kg)
self.g = 9.8 # 重力加速度(m/s^2)
self.I_xx = 0.0211 # x轴转动惯量
self.I_yy = 0.0219 # y轴转动惯量
self.I_zz = 0.0366 # z轴转动惯量
self.J_RP = 0.0001287 # 转子惯性

# 初始位置
self.Pos_z = -100 # 初始高度
self.Pos_x = 0
self.Pos_y = 0

# 初始姿态
self.phi0 = 0
self.theta0 = 0
self.psi0 = 0

# 电机模型
def motor_model(throttle, params):
# 计算稳态转速
return (params.C_r * throttle + params.w_b)

# 控制效率模型
def control_efficiency(w1, w2, w3, w4, params):
# 计算总拉力和力矩
f = params.c_T * (w1 ** 2 + w2 ** 2 + w3 ** 2 + w4 ** 2)
tau_x = params.d * params.c_T * (math.sqrt(2) / 2) * (-w1 ** 2 + w2 ** 2 + w3 ** 2 – w4 ** 2)
tau_y = params.d * params.c_T * (math.sqrt(2) / 2) * (w1 ** 2 – w2 ** 2 + w3 ** 2 – w4 ** 2)
tau_z = params.c_M * (w1 ** 2 + w2 ** 2 – w3 ** 2 – w4 ** 2)
return f, tau_x, tau_y, tau_z

# 姿态动力学模型
def attitude_dynamics(w1, w2, w3, w4, tau_x, tau_y, tau_z, p, q, r, params):
# 计算总转动惯量
Omega = -w1 + w2 – w3 + w4
# 计算角加速度
p_dot = (1 / params.I_xx) * (tau_x + q * r * (params.I_yy – params.I_zz) – params.J_RP * q * Omega)
q_dot = (1 / params.I_yy) * (tau_y + p * r * (params.I_zz – params.I_xx) + params.J_RP * p * Omega)
r_dot = (1 / params.I_zz) * (tau_z + p * q * (params.I_xx – params.I_yy))
return p_dot, q_dot, r_dot

# 位置动力学模型
def position_dynamics(phi, theta, psi, f, params):
# 计算线加速度
v_x_dot = -f * (1 / params.m) * (math.cos(psi) * math.sin(theta) * math.cos(phi) + math.sin(psi) * math.sin(phi))
v_y_dot = -f * (1 / params.m) * (math.sin(psi) * math.sin(theta) * math.cos(phi) – math.cos(psi) * math.sin(phi))
v_z_dot = -params.g + f * (1 / params.m) * math.cos(phi) * math.cos(theta)
return v_x_dot, v_y_dot, v_z_dot

# 运动学模型
def kinematics(p, q, r, phi, theta, psi):
# 计算姿态角速度
phi_dot = p + q * math.tan(theta) * math.sin(phi) + r * math.tan(theta) * math.cos(phi)
theta_dot = q * math.cos(phi) – r * math.sin(phi)
psi_dot = (q * math.sin(phi) + r * math.cos(phi)) / math.cos(theta)
return phi_dot, theta_dot, psi_dot

# 主仿真函数
def simulate_quadcopter(t_total, throttle, dt=0.01):
params = QuadcopterParams()
steps = int(t_total / dt)

# 初始化状态数组
states = {
't': np.zeros(steps),
'x': np.zeros(steps), 'y': np.zeros(steps), 'z': np.full(steps, params.Pos_z),
'vx': np.zeros(steps), 'vy': np.zeros(steps), 'vz': np.zeros(steps),
'phi': np.zeros(steps), 'theta': np.zeros(steps), 'psi': np.zeros(steps),
'p': np.zeros(steps), 'q': np.zeros(steps), 'r': np.zeros(steps),
'w1': np.zeros(steps), 'w2': np.zeros(steps), 'w3': np.zeros(steps), 'w4': np.zeros(steps),
'f': np.zeros(steps), 'ax': np.zeros(steps), 'ay': np.zeros(steps), 'az': np.zeros(steps)
}

# 初始状态
w_steady = motor_model(throttle, params)
w1 = w2 = w3 = w4 = w_steady

# 实际使用的步数
actual_steps = steps

# 主仿真循环
for step in range(1, steps):
# 1. 更新电机转速（一阶响应模型）
w1 = w1 + (w_steady – w1) * dt / params.T_m
w2 = w2 + (w_steady – w2) * dt / params.T_m
w3 = w3 + (w_steady – w3) * dt / params.T_m
w4 = w4 + (w_steady – w4) * dt / params.T_m

# 2. 计算拉力和力矩
f, tau_x, tau_y, tau_z = control_efficiency(w1, w2, w3, w4, params)

# 3. 姿态动力学
p_dot, q_dot, r_dot = attitude_dynamics(w1, w2, w3, w4, tau_x, tau_y, tau_z,
states['p'][step – 1], states['q'][step – 1], states['r'][step – 1],
params)

# 4. 位置动力学
ax, ay, az = position_dynamics(states['phi'][step – 1], states['theta'][step – 1], states['psi'][step – 1], f,
params)

# 5. 运动学
phi_dot, theta_dot, psi_dot = kinematics(states['p'][step – 1], states['q'][step – 1], states['r'][step – 1],
states['phi'][step – 1], states['theta'][step – 1],
states['psi'][step – 1])

# 状态更新（数值积分）
states['p'][step] = states['p'][step – 1] + p_dot * dt
states['q'][step] = states['q'][step – 1] + q_dot * dt
states['r'][step] = states['r'][step – 1] + r_dot * dt

states['phi'][step] = states['phi'][step – 1] + phi_dot * dt
states['theta'][step] = states['theta'][step – 1] + theta_dot * dt
states['psi'][step] = states['psi'][step – 1] + psi_dot * dt

states['vx'][step] = states['vx'][step – 1] + ax * dt
states['vy'][step] = states['vy'][step – 1] + ay * dt
states['vz'][step] = states['vz'][step – 1] + az * dt

states['x'][step] = states['x'][step – 1] + states['vx'][step] * dt
states['y'][step] = states['y'][step – 1] + states['vy'][step] * dt
states['z'][step] = states['z'][step – 1] + states['vz'][step] * dt

# 地面碰撞检测
if states['z'][step] > 0:
states['z'][step] = 0
states['vz'][step] = 0
states['az'][step] = 0

# 存储其他数据
states['w1'][step] = w1
states['w2'][step] = w2
states['w3'][step] = w3
states['w4'][step] = w4
states['f'][step] = f
states['ax'][step] = ax
states['ay'][step] = ay
states['az'][step] = az
states['t'][step] = step * dt

# 提前终止如果无人机已起飞并稳定
if step > 100 and abs(states['z'][step] – states['z'][step – 10]) < 0.1:
actual_steps = step + 1 # 包括索引0到step
break

# 截断所有数组到实际步数
for key in states:
states[key] = states[key][:actual_steps]

return states

# 可视化函数
def visualize_results(states, throttle):
# 创建3D轨迹图
scatter = go.Scatter3d(
x=states['x'],
y=states['y'],
z=states['z'],
mode='lines',
line=dict(
width=4,
color=np.linspace(0, 1, len(states['z'])),
colorscale='Viridis'
),
name='轨迹'
)

# 添加起点和终点标记
start_marker = go.Scatter3d(
x=[states['x'][0]],
y=[states['y'][0]],
z=[states['z'][0]],
mode='markers',
marker=dict(size=6, color='green'),
name='起点'
)

end_marker = go.Scatter3d(
x=[states['x'][-1]],
y=[states['y'][-1]],
z=[states['z'][-1]],
mode='markers',
marker=dict(size=6, color='red'),
name='终点'
)

fig = go.Figure(data=[scatter, start_marker, end_marker])

# 设置图表布局
fig.update_layout(
scene=dict(
xaxis=dict(title='X位置 (米)'),
yaxis=dict(title='Y位置 (米)'),
zaxis=dict(title='高度 (米)'),
aspectratio=dict(x=2, y=1, z=1),
camera=dict(eye=dict(x=1.5, y=1.5, z=0.8))
),
title=f'四旋翼飞行轨迹 (油门={throttle})',
height=700
)

# 在Streamlit中显示
st.plotly_chart(fig, use_container_width=True)

# 创建2D图表
st.subheader('飞行动态指标')

# 高度和速度
col1, col2 = st.columns(2)
with col1:
st.markdown("#### 高度")
fig, ax = plt.subplots()
ax.plot(states['t'], states['z'], 'b-')
ax.set_xlabel('时间 (秒)')
ax.set_ylabel('高度 (米)')
ax.grid(True)
ax.set_title('高度变化')
st.pyplot(fig)

with col2:
st.markdown("#### 垂直速度")
fig, ax = plt.subplots()
ax.plot(states['t'], states['vz'], 'g-')
ax.set_xlabel('时间 (秒)')
ax.set_ylabel('垂直速度 (米/秒)')
ax.grid(True)
ax.set_title('垂直速度变化')
st.pyplot(fig)

# 姿态角度
st.markdown("#### 姿态角度")
fig, ax = plt.subplots()
ax.plot(states['t'], np.degrees(states['phi']), 'r-', label='滚转角 φ')
ax.plot(states['t'], np.degrees(states['theta']), 'g-', label='俯仰角 θ')
ax.plot(states['t'], np.degrees(states['psi']), 'b-', label='偏航角 ψ')
ax.set_xlabel('时间 (秒)')
ax.set_ylabel('角度 (度)')
ax.legend()
ax.grid(True)
st.pyplot(fig)

# 角速度
st.markdown("#### 角速度")
fig, ax = plt.subplots()
ax.plot(states['t'], states['p'], 'm-', label='x轴角速度 p')
ax.plot(states['t'], states['q'], 'c-', label='y轴角速度 q')
ax.plot(states['t'], states['r'], 'y-', label='z轴角速度 r')
ax.set_xlabel('时间 (秒)')
ax.set_ylabel('角速度 (弧度/秒)')
ax.legend()
ax.grid(True)
st.pyplot(fig)

# 螺旋桨转速
st.markdown("#### 螺旋桨转速")
fig, ax = plt.subplots()
ax.plot(states['t'], states['w1'], 'r-', label='螺旋桨1')
ax.plot(states['t'], states['w2'], 'g-', label='螺旋桨2')
ax.plot(states['t'], states['w3'], 'b-', label='螺旋桨3')
ax.plot(states['t'], states['w4'], 'm-', label='螺旋桨4')
ax.set_xlabel('时间 (秒)')
ax.set_ylabel('角速度 (弧度/秒)')
ax.legend()
ax.grid(True)
st.pyplot(fig)

# 显示关键指标
st.subheader('飞行摘要')
final_altitude = states['z'][-1]
max_altitude = max(states['z'])
flight_time = states['t'][-1]

col1, col2, col3 = st.columns(3)
col1.metric("最终高度", f"{final_altitude:.2f} 米")
col2.metric("峰值高度", f"{max_altitude:.2f} 米")
col3.metric("飞行时间", f"{flight_time:.1f} 秒")

# 显示原始数据
if st.checkbox('显示原始飞行数据'):
data = {
'时间': states['t'],
'X位置': states['x'],
'Y位置': states['y'],
'高度': states['z'],
'油门': np.full_like(states['t'], throttle)
}
st.dataframe(data)

# Streamlit应用主函数
def main():
st.title("🎮 四旋翼无人机飞行仿真器")
st.markdown("""
本仿真器基于四旋翼无人机的物理参数模拟其飞行动态。
调整油门设置可以观察其对无人机飞行特性的影响。
""")

# 创建参数输入侧边栏
st.sidebar.header("四旋翼参数设置")

# 用户可调整参数
throttle = st.sidebar.slider("油门输入 (0.4-0.7)", 0.4, 0.7, 0.55, 0.01,
help="油门控制输入 (0.4≈悬停, 0.7≈爬升)")

flight_time = st.sidebar.slider("仿真时间 (秒)", 2.0, 30.0, 10.0, 0.5)

mass = st.sidebar.slider("无人机质量 (kg)", 0.5, 3.0, 1.4, 0.1)

propeller_size = st.sidebar.slider("螺旋桨尺寸 (米)", 0.1, 0.5, 0.225, 0.01,
help="机体中心到电机的距离")

# 显示预设参数
st.sidebar.header("物理参数")
st.sidebar.write(f"拉力系数: 1.105e-5 N·s²/rad²")
st.sidebar.write(f"力矩系数: 1.779e-7 N·m·s²/rad²")
st.sidebar.write(f"重力加速度: 9.8 m/s²")

# 添加开发者备注
st.sidebar.markdown("—")
st.sidebar.info("""
**仿真说明:**
– 无人机从地下100米处开始飞行
– 更高的油门值会产生更快的爬升速度
– 当无人机达到稳定高度时仿真会自动停止
""")

# 创建开始仿真按钮
if st.button('开始飞行仿真', use_container_width=True):
with st.spinner('仿真运行中…'):
# 创建参数对象
params = QuadcopterParams()
params.m = mass
params.d = propeller_size

# 运行仿真
states = simulate_quadcopter(flight_time, throttle)

# 显示结果
if len(states['t']) > 10:
# 显示起飞成功消息
if states['z'][-1] >= 0:
st.success(f"🚁 无人机成功爬升至 {states['z'][-1]:.1f}米高度!")
else:
st.warning(f"⚠️ 无人机仍在 {states['z'][-1]:.1f}米高度 – 请增加油门值!")

# 显示可视化
visualize_results(states, throttle)
else:
st.error("仿真失败，请尝试不同的参数。")

if __name__ == "__main__":
main()