深度学习 — 过拟合与欠拟合
文章目录
- 深度学习 — 过拟合与欠拟合
- 一.概念
-
- 1.1 过拟合
- 1.2 欠拟合
- 1.3 判断方式
- 二,解决欠拟合
- 三,解决过拟合
-
- 3.1 L2正则化
-
- 3.1.1 定义以及作用
- 3.1.2 代码
- 3.2 L1正则化
- 3.3 L1与L2对比
- 3.4 Dropout
-
- 示例
- 3.5 数据增强
-
- 3.5.1 图片缩放
- 3.5.2 随机裁剪
- 3.5.3 随机水平翻转
- 3.5.4 调整图片颜色
- 3.5.5 随机旋转
- 3.5.6 图片转Tensor
- 3.5.7 Tensor转图片
- 3.5.8 归一化
- 3.5.9 数据增强整合
一.概念
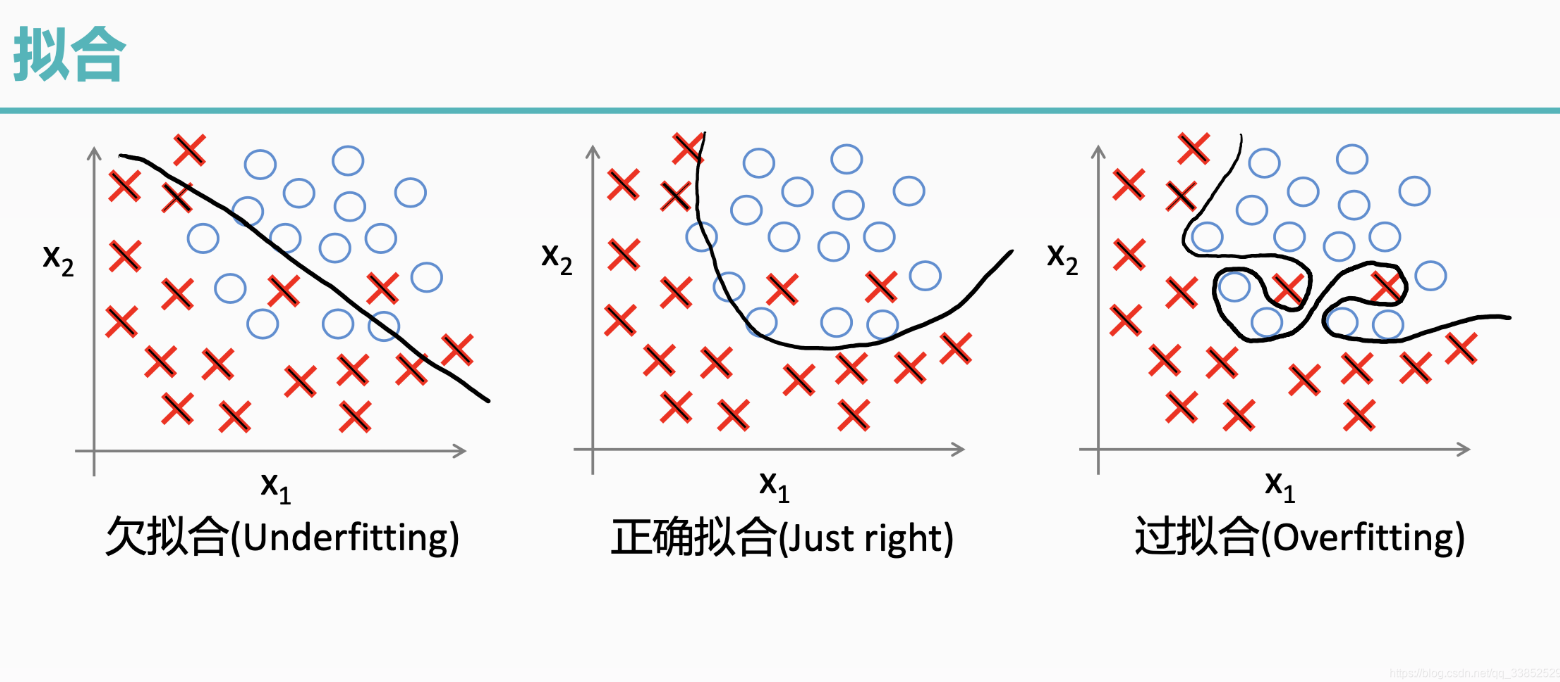
1.1 过拟合
过拟合是指模型对训练数据拟合能力很强并表现很好,但在测试数据上表现较差。
过拟合常见原因有:
1.2 欠拟合
欠拟合是由于模型学习能力不足,无法充分捕捉数据中的复杂关系。
1.3 判断方式
过拟合
训练误差低,但验证时误差高。模型在训练数据上表现很好,但在验证数据上表现不佳,说明模型可能过度拟合了训练数据中的噪声或特定模式。
欠拟合
训练误差和测试误差都高。模型在训练数据和测试数据上的表现都不好,说明模型可能太简单,无法捕捉到数据中的复杂模式。
二,解决欠拟合
欠拟合的解决思路比较直接:
三,解决过拟合
避免模型参数过大是防止过拟合的关键步骤之一。
模型的复杂度主要由权重w决定,而不是偏置b。偏置只是对模型输出的平移,不会导致模型过度拟合数据。
怎么控制权重w,使w在比较小的范围内?
考虑损失函数,损失函数的目的是使预测值与真实值无限接近,如果在原来的损失函数上添加一个非0的变量
L
1
(
y
^
,
y
)
=
L
(
y
^
,
y
)
+
f
(
w
)
L_1(\\hat{y},y) = L(\\hat{y},y) + f(w)
L1(y^,y)=L(y^,y)+f(w) 其中
f
(
w
)
f(w)
f(w)是关于权重w的函数,
f
(
w
)
>
0
f(w)>0
f(w)>0
要使L1变小,就要使L变小的同时,也要使
f
(
w
)
f(w)
f(w)变小。从而控制权重w在较小的范围内。
3.1 L2正则化
L2 正则化通过在损失函数中添加权重参数的平方和来实现,目标是惩罚过大的参数值。
3.1.1 定义以及作用
| 原始损失函数 | 模型未加正则化的损失函数(如 MSE、交叉熵) |
L ( θ ) L(\\theta) L(θ) |
仅衡量模型在训练数据上的误差。 |
| L2 正则化项 | 所有权重参数的平方和 |
1 2 ∑ i θ i 2 \\frac{1}{2} \\sum_i \\theta_i^2 21∑iθi2 |
惩罚大权重,防止模型复杂度过高。 |
| 总损失函数 | 原始损失 + L2 正则化项 |
L total ( θ ) = L ( θ ) + λ 2 ∑ i θ i 2 L_{\\text{total}}(\\theta) = L(\\theta) + \\frac{\\lambda}{2} \\sum_i \\theta_i^2 Ltotal(θ)=L(θ)+2λ∑iθi2 |
加入惩罚项,平衡拟合能力与复杂度。 |
| 梯度更新规则 | 参数更新时考虑原始梯度 + L2 项的梯度 |
θ t + 1 = θ t − η ( ∇ L ( θ t ) + λ θ t ) \\theta_{t+1} = \\theta_t – \\eta \\left( \\nabla L(\\theta_t) + \\lambda \\theta_t \\right) θt+1=θt−η(∇L(θt)+λθt) |
每次更新都“衰减”参数(乘以
1 − η λ 1 – \\eta \\lambda 1−ηλ),防止权重过大。 |
|
1 2 \\frac{1}{2} 21 的作用 |
简化梯度计算 |
∂ ∂ θ i ( 1 2 θ i 2 ) = θ i \\frac{\\partial}{\\partial \\theta_i} \\left( \\frac{1}{2} \\theta_i^2 \\right) = \\theta_i ∂θi∂(21θi2)=θi |
消去系数 2,使梯度更新公式更简洁(避免
2 λ θ i 2\\lambda \\theta_i 2λθi)。 |
| 防止过拟合 | 抑制权重过大,降低模型对训练噪声的敏感性 | – | 权重越小,模型对输入扰动越不敏感,泛化能力增强。 |
| 限制模型复杂度 | 强制权重接近 0,避免过拟合 | – | 通过惩罚大权重,减少模型自由度,降低 VC 维。 |
| 提高泛化能力 | 在训练集和测试集上表现更均衡 | – | 正则化项使模型更关注数据的真实规律,而非噪声。 |
| 平滑权重分布 | 权重逐渐缩小但不直接为 0 | – | 保留所有特征贡献,避免稀疏性(与 L1 不同),使模型更平滑。 |
3.1.2 代码
import torch
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt
# 设置随机种子以保证可重复性
torch.manual_seed(42)
# 生成随机数据
n_samples = 100
n_features = 20
X = torch.randn(n_samples, n_features) # 输入数据
y = torch.randn(n_samples, 1) # 目标值
# 定义一个简单的全连接神经网络
class SimpleNet(nn.Module):
def __init__(self):
super(SimpleNet, self).__init__()
self.fc1 = nn.Linear(n_features, 50)
self.fc2 = nn.Linear(50, 1)
def forward(self, x):
x = torch.relu(self.fc1(x))
return self.fc2(x)
# 训练函数
def train_model(use_l2=False, weight_decay=0.01, n_epochs=100):
# 初始化模型
model = SimpleNet()
criterion = nn.MSELoss() # 损失函数(均方误差)
# 选择优化器
if use_l2:
optimizer = optim.SGD(model.parameters(), lr=0.01, weight_decay=weight_decay) # 使用 L2 正则化
else:
optimizer = optim.SGD(model.parameters(), lr=0.01) # 不使用 L2 正则化
# 记录训练损失
train_losses = []
# 训练过程
for epoch in range(n_epochs):
optimizer.zero_grad() # 清空梯度
outputs = model(X) # 前向传播
loss = criterion(outputs, y) # 计算损失
loss.backward() # 反向传播
optimizer.step() # 更新参数
train_losses.append(loss.item()) # 记录损失
if (epoch + 1) % 10 == 0:
print(f'Epoch [{epoch + 1}/{n_epochs}], Loss: {loss.item():.4f}')
return train_losses
# 训练并比较两种模型
train_losses_no_l2 = train_model(use_l2=False) # 不使用 L2 正则化
train_losses_with_l2 = train_model(use_l2=True, weight_decay=0.01) # 使用 L2 正则化
# 绘制训练损失曲线
plt.plot(train_losses_no_l2, label='Without L2 Regularization')
plt.plot(train_losses_with_l2, label='With L2 Regularization')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.title('Training Loss: L2 Regularization vs No Regularization')
plt.legend()
plt.show()
3.2 L1正则化
设模型的原始损失函数为
L
(
θ
)
L(\\theta)
L(θ),其中
θ
\\theta
θ 表示模型权重参数,则加入 L1 正则化后的损失函数表示为:
L
total
(
θ
)
=
L
(
θ
)
+
λ
∑
i
∣
θ
i
∣
L_{\\text{total}}(\\theta) = L(\\theta) + \\lambda \\sum_{i} |\\theta_i|
Ltotal(θ)=L(θ)+λi∑∣θi∣
- 梯度更新 在 L1 正则化下,梯度更新时的公式是:
θ
t
+
1
=
θ
t
−
η
(
∇
L
(
θ
t
)
+
λ
⋅
sign
(
θ
t
)
)
\\theta_{t+1} = \\theta_t – \\eta \\left( \\nabla L(\\theta_t) + \\lambda \\cdot \\text{sign}(\\theta_t) \\right)
θt+1=θt−η(∇L(θt)+λ⋅sign(θt)) - 作用:
稀疏性:L1 正则化的一个显著特性是它会促使许多权重参数变为 零。这是因为 L1 正则化倾向于将权重绝对值缩小到零,使得模型只保留对结果最重要的特征,而将其他不相关的特征权重设为零,从而实现 特征选择 的功能。
防止过拟合:通过限制权重的绝对值,L1 正则化减少了模型的复杂度,使其不容易过拟合训练数据。相比于 L2 正则化,L1 正则化更倾向于将某些权重完全移除,而不是减小它们的值。
简化模型:由于 L1 正则化会将一些权重变为零,因此模型最终会变得更加简单,仅依赖于少数重要特征。这对于高维度数据特别有用,尤其是在特征数量远多于样本数量的情况下。
特征选择:因为 L1 正则化会将部分权重置零,因此它天然具有特征选择的能力,有助于自动筛选出对模型预测最重要的特征。
3.3 L1与L2对比
| 惩罚项 |
∑ i θ i 2 \\sum_i \\theta_i^2 ∑iθi2 |
∑ _ i θ _ i \\sum\\_i \\theta\\_i ∑_iθ_i |
| 效果 | 权重平滑趋近于 0 | 权重稀疏(部分变为 0) |
| 梯度 |
λ θ i \\lambda \\theta_i λθi |
λ ⋅ sign ( θ i ) \\lambda \\cdot \\text{sign}(\\theta_i) λ⋅sign(θi) |
| 适用场景 | 特征共线性强、需要保留所有特征 | 特征选择(自动忽略无关特征) |
3.4 Dropout
Dropout 的工作流程如下:
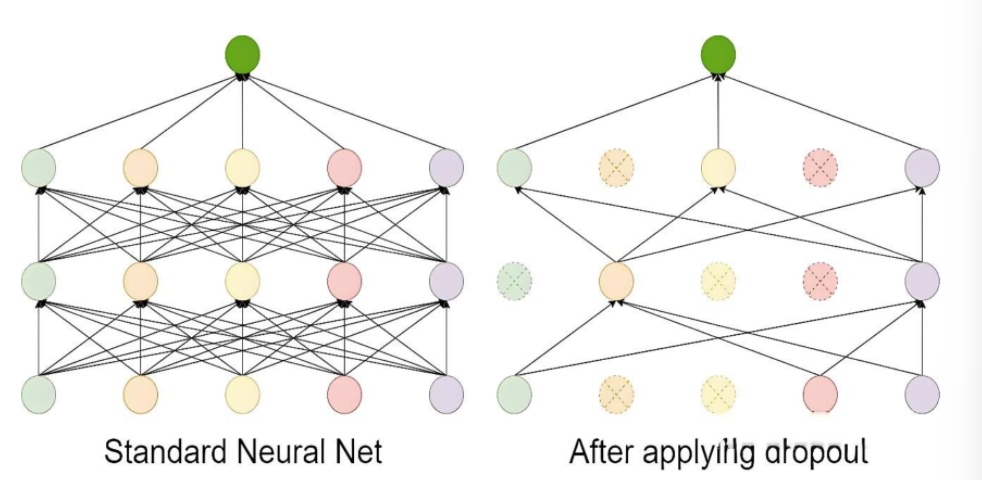 Dropout 是一种在训练过程中随机丢弃部分神经元的技术。它通过减少神经元之间的依赖来防止模型过于复杂,从而避免过拟合。
Dropout 是一种在训练过程中随机丢弃部分神经元的技术。它通过减少神经元之间的依赖来防止模型过于复杂,从而避免过拟合。import torch
import torch.nn as nn
def test01():
x=torch.randint(1,10,(5,5),dtype=torch.float)
dropout=nn.Dropout(p=0.5)
print(x)
print(dropout(x))
if __name__ == '__main__':
test01()
示例
对图片进行随机丢弃
import torch
from torch import nn
from PIL import Image
from torchvision import transforms
import os
from matplotlib import pyplot as plt
torch.manual_seed(42)
def load_img(path, resize=(224, 224)):
pil_img = Image.open(path).convert('RGB')
print("Original image size:", pil_img.size) # 打印原始尺寸
transform = transforms.Compose([
transforms.Resize(resize),
transforms.ToTensor() # 转换为Tensor并自动归一化到[0,1]
])
return transform(pil_img) # 返回[C,H,W]格式的tensor
if __name__ == '__main__':
dirpath = os.path.dirname(__file__)
path = os.path.join(dirpath, 'img', 'torch-fcnn/fcnn-demo/100.jpg') # 使用os.path.join更安全
# 加载图像 (已经是[0,1]范围的Tensor)
trans_img = load_img(path)
# 添加batch维度 [1, C, H, W],因为Dropout默认需要4D输入
trans_img = trans_img.unsqueeze(0)
# 创建Dropout层
dropout = nn.Dropout2d(p=0.2)
drop_img = dropout(trans_img)
# 移除batch维度并转换为[H,W,C]格式供matplotlib显示
trans_img = trans_img.squeeze(0).permute(1, 2, 0).numpy()
drop_img = drop_img.squeeze(0).permute(1, 2, 0).numpy()
# 确保数据在[0,1]范围内
drop_img = drop_img.clip(0, 1)
# 显示图像
fig = plt.figure(figsize=(10, 5))
ax1 = fig.add_subplot(1, 2, 1)
ax1.imshow(trans_img)
ax2 = fig.add_subplot(1, 2, 2)
ax2.imshow(drop_img)
plt.show()
3.5 数据增强
样本数量不足(即训练数据过少)是导致过拟合(Overfitting)的常见原因之一,可以从以下角度理解:
- 当训练数据过少时,模型容易“记住”有限的样本(包括噪声和无关细节),而非学习通用的规律。
- 简单模型更可能捕捉真实规律,但数据不足时,复杂模型会倾向于拟合训练集中的偶然性模式(噪声)。
- 样本不足时,训练集的分布可能与真实分布偏差较大,导致模型学到错误的规律。
- 小数据集中,个别样本的噪声(如标注错误、异常值)会被放大,模型可能将噪声误认为规律。
数据增强(Data Augmentation)是一种通过人工生成或修改训练数据来增加数据集多样性的技术,常用于解决过拟合问题。数据增强通过“模拟”更多训练数据,迫使模型学习泛化性更强的规律,而非训练集中的偶然性模式。其本质是一种低成本的正则化手段,尤其在数据稀缺时效果显著。
在了解计算机如何处理图像之前,需要先了解图像的构成元素。
图像是由像素点组成的,每个像素点的值范围为: [0, 255], 像素值越大意味着较亮。比如一张 200×200 的图像, 则是由 40000 个像素点组成, 如果每个像素点都是 0 的话, 意味着这是一张全黑的图像。
我们看到的彩色图一般都是多通道的图像, 所谓多通道可以理解为图像由多个不同的图像层叠加而成, 例如我们看到的彩色图像一般都是由 RGB 三个通道组成的,还有一些图像具有 RGBA 四个通道,最后一个通道为透明通道,该值越小,则图像越透明。
数据增强是提高模型泛化能力(鲁棒性)的一种有效方法,尤其在图像分类、目标检测等任务中。数据增强可以模拟更多的训练样本,从而减少过拟合风险。数据增强通过torchvision.transforms模块来实现。
3.5.1 图片缩放
def test01():
path="torch-fcnn/fcnn-demo/datasets/100.jpg"
img=Image.open(path)
print(img.size)
transform=transforms.Compose([
transforms.Resize((224,224)),
transforms.ToTensor()
])
t_img=transform(img)
print(t_img.shape)
t_img = torch.permute(t_img, (1, 2, 0))
plt.imshow(t_img)
plt.show()
3.5.2 随机裁剪
def test02():
path="torch-fcnn/fcnn-demo/datasets/100.jpg"
img=Image.open(path)
print(img.size)
transform=transforms.Compose([
transforms.RandomCrop((224,224)),
transforms.ToTensor()
])
t_img=transform(img)
# print(t_img.shape)
t_img = torch.permute(t_img, (1, 2, 0))
plt.imshow(t_img)
plt.show()
3.5.3 随机水平翻转
def test03():
path="torch-fcnn/fcnn-demo/datasets/100.jpg"
img=Image.open(path)
print(img.size)
transform=transforms.Compose([
transforms.RandomHorizontalFlip(p=1),
transforms.ToTensor()
])
t_img=transform(img)
# print(t_img.shape)
t_img = torch.permute(t_img, (1, 2, 0))
plt.imshow(t_img)
plt.show()
3.5.4 调整图片颜色
img = Image.open('./img/100.jpg')
transform = transforms.Compose([transforms.ColorJitter(brightness=0.2, contrast=0.2, saturation=0.2, hue=0.2), transforms.ToTensor()])
r_img = transform(img)
print(r_img.shape)
r_img = r_img.permute(1, 2, 0)
plt.imshow(r_img)
plt.show()
3.5.5 随机旋转
def test04():
path="torch-fcnn/fcnn-demo/datasets/100.jpg"
img=Image.open(path)
print(img.size)
transform=transforms.RandomRotation((30,60),
expand=False,
center=None,
fill=0
)
3.5.6 图片转Tensor
def test05():
t=torch.randn(3,224,224)
transform=transforms.Compose([
# 转换为PIL图片
transforms.ToPILImage(),
transforms.ToTensor(),
])
t_img=transform(t)
# print(t_img.shape)
t_img = torch.permute(t_img, (1, 2, 0))
plt.imshow(t_img)
plt.show()
3.5.7 Tensor转图片
import torch
from PIL import Image
from torchvision import transforms
def test002():
# 1. 随机一个数据表示图片
img_tensor = torch.randn(3, 224, 224)
# 2. 创建一个transforms
transform = transforms.ToPILImage()
# 3. 转换为图片
img = transform(img_tensor)
img.show()
# 4. 保存图片
img.save("./test.jpg")
if __name__ == "__main__":
test002()
3.5.8 归一化
def test06():
path="torch-fcnn/fcnn-demo/datasets/100.jpg"
img=Image.open(path)
print(img.size)
t=torch.randn(3,224,224)
transform = transforms.Compose([
transforms.ToTensor(),
# 归一化
transforms.Normalize(mean=[0.485, 0.456, 0.406],
std=[0.229, 0.224, 0.225])
])
t_img=transform(t)
# print(t_img.shape)
t_img = torch.permute(t_img, (1, 2, 0))
plt.imshow(t_img)
plt.show()
3.5.9 数据增强整合
from PIL import Image
from pathlib import Path
import matplotlib.pyplot as plt
import numpy as np
import torch
from torchvision import transforms, datasets, utils
def test01():
# 定义数据增强和归一化
transform = transforms.Compose(
[
transforms.RandomHorizontalFlip(), # 随机水平翻转
transforms.RandomRotation(10), # 随机旋转 ±10 度
transforms.RandomResizedCrop(
32, scale=(0.8, 1.0)
), # 随机裁剪到 32×32,缩放比例在0.8到1.0之间
transforms.ColorJitter(
brightness=0.2, contrast=0.2, saturation=0.2, hue=0.1
), # 随机调整亮度、对比度、饱和度、色调
transforms.ToTensor(), # 转换为 Tensor
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5)), # 归一化,这是一种常见的经验设置,适用于数据范围 [0, 1],使其映射到 [-1, 1]
]
)
# 加载 CIFAR-10 数据集,并应用数据增强
trainset = datasets.CIFAR10(root="./cifar10_data", train=True, download=True, transform=transform)
dataloader = DataLoader(trainset, batch_size=4, shuffle=False)
# 获取一个批次的数据
images, labels = next(iter(dataloader))
# 还原图片并显示
plt.figure(figsize=(10, 5))
for i in range(4):
# 反归一化:将像素值从 [-1, 1] 还原到 [0, 1]
img = images[i] / 2 + 0.5
# 转换为 PIL 图像
img_pil = transforms.ToPILImage()(img)
# 显示图片
plt.subplot(1, 4, i + 1)
plt.imshow(img_pil)
plt.axis('off')
plt.title(f'Label: {labels[i]}')
plt.show()
if __name__ == "__main__":
test01()
 网硕互联帮助中心
网硕互联帮助中心




评论前必须登录!
注册